Лабораторна робота № 2.

Тема: Дослідження кола однофазного змінного струму з послідовним з’єднанням споживачів.

Мета: 1. Перевірити закон Ома для кола з послідовно ввімкнутими споживачами. 2. Дослідити, як впливає зміна ємності С на величину струму, опору, потужності, кута зсуву фаз, коефіцієнта потужності у колі і напруги на ділянках кола. 3. Дослідити, за яких умов виникає резонанс напруг у колі з послідовним з’єднанням споживачів. 4. Навчитися будувати векторні діаграми напруг та резонансні криві. 5. Вивчити методику розрахунків електричного кола однофазного струму з послідовно з’єднаними опорами.

Прилади та матеріали: лабораторний стенд з електротехніки.

Робочі схеми: т еоретичні відомості:

Одним з основних параметрів якого-небудь електричного кола є його електричний опір, який характеризує протидію кола електричному струмові.

Електричний опір R в колі постійного струму дорівнює відношенню напруги U до сили струму І (Закон Ома для ділянки кола). У такому випадку R називають омічним опором; його величина залежить від матеріалу, розмірів і форми провідника. Для однорідного за складом провідника при сталому поперечному перерізі S і довжині l провідника R=l/S, де  - питомий опір, яким характеризується матеріал з якого виготовлений провідник.

Електричний опір у колі із змінного струму дорівнює відношенню напруги U до сили струму I i називається повним опором Z кола. Повний опір характеризується активною R і реактивною Х складовими опору: . Активний опір за величиною дорівнює відношенню активної потужності Р, яка споживається ділянкою кола, до квадрата діючого значення сили струму І, що проходить по колу: R=P/I².

Активний опір звичайно більший від омічного (при сталій напрузі) внаслідок поверхневого ефекту, ефекту близькості і втрат енергії в змінному електромагнітному колі на колові струми і гістерезис (магнітний і діелектричний).

А

ктивний опір окремих прямолінійних діамагнітних провідників малої довжини для технічної частоти 50 Гц має різницю настільки малу, що практично нею нехтують. Але цього не можна допускати для провідників, намотаних у котушки з феромагнітним сердечником, бо для них активний опір більший від омічного на 3-15%. Особливо з цим треба рахуватися у випадку змінних струмів високої частоти, для якої активний опір у кілька разів більший від омічного.

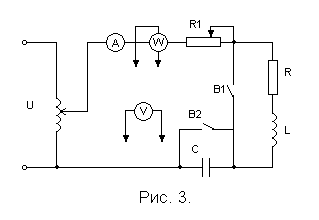
Реальна котушка має активний опір R та індуктивність L, тому під час вмикання її у мережу змінного струму (рис. 3 - вимикач В2 замкнуто, В1 розімкнуто, реостат R1 виведено) по колу котушки проходитиме струм, який є наслідком дії прикладеної зовнішньої напруги і е. р. с. самоіндукції, що виникає в самій котушці.

С

трум в колі за законом Ома , де - повний опір ділянки кола.

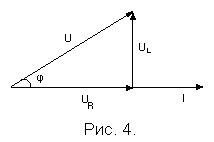
З трикутника напруг (рис. 4) маємо , де U_R=IR=P/I. Кут зсуву фаз між напругою і струмом можна визначити із співвідношення сторін трикутника, а саме: tg=U_L/U_R=X_L/R, або cos=U_R/U=R/Z.

Аналізуючи цю залежність, приходимо до висновку: якщо X_L=L=0, то =0, тобто в даному колі не буде зсуву фаз між напругою і струмом; якщо R=0 то =90, а якщо R_L>0 i X_L>0, то >0, тобто у колі з активним та індуктивним опорами напруга випереджає струм на кут <90.

Миттєва потужність у цьому колі дорівнює добутку миттєвих значень напруги і струму: p=ui=U_mI_msin(t+)sint=UIcos-UІcos(2t+). Середня, або активна, потужність Р у колі за період Т: P=.

З останнього виразу видно, що активна потужність залежить не тільки від діючих значень напруги і струму, а й від коефіцієнта потужності.

У котушці без осердя повний опір Z_L, активний опір R, iндуктивний опір X_L і її індуктивність залишаються сталими при зміні величини струму у колі за сталої частоти.

У котушці із стальним осердям при різній величині струму І_L і сталій частоті індуктивність L змінюється, що є наслідком зміни магнітної проникності сталі. Змінюються також повний опір Z_L, активний опір R, і iндуктивний опір X_L. Оскільки в котушці є втрати не тільки у міді обмотки Р_М, а й у сталі осердя Р_СТ на коерцитивні сили і вихрові струми, повна потужність втрат у котушці Р=Р_М+Р_СТ=І²R=UIcos.

З цього співвідношення визначимо активний опір котушки де R_M - активний опір обмотки, R_CT - опір, еквівалентний опорові втрат у сталі осердя.

Вимірявши потужність втрат у котушці без осердя Р_М і з осердям Р, можна визначити втрати у сталі осердя при даній величині струму: Р_СТ=Р-Р_М, які змінюються із зміною величини струму у котушці нелінійно. В зв’язку з цим із зміною струму змінюються повний, активний та індуктивний опори. Отже, котушка із стальним осердям є нелінійним елементом у колі. Щоб визначити активний та індуктивний опори котушки із стальним осердям для будь-якої величини струму, треба спочатку дослідити і побудувати в масштабі графіки для цієї котушки U=f(I) та Z=f(I).

Ємність у колі змінного струму утворює реактивний опір Х_С=(С)^-1, який викликає від’ємний зсув фаз між напругою і струмом на кут =-90, тобто напруга за фазою відстає від струму на чверть періоду.

Д

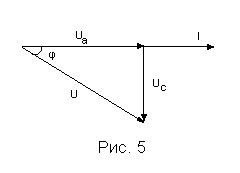
ля електричного кола з послідовно з’єднаними активним опором R1, ємнісним опором Х_С (рис. 3 - вимикач В1 замкнуто, В2 розімкнуто) силу струму можна визначити за законом Ома: Кут зсуву фаз між напругою і струмом (рис. 5) визначимо із співвідношення звідки , або із співвідношення

Потужності у колі: активна P=I²R₁=IU_a=UIcos, реактивна Q_C=I²X_C=U_CIsin, повна

Для електричного кола з послідовно з’єднаними активним опором R₁, повним опором котушки Z_K i ємнісним опором X_C (рис. 3 - вимикачі ВІ i В2 розімкнуто) векторні діаграми напруг зображено на рис.6 ( а – коли X_L>X_C, б – коли X_L<X_C).

З векторних діаграм видно, що реактивна складова напруги U_p дорівнює різниці реактивних напруг, iндуктивної i ємнісної, i має знак більшої з них: U_p=U_L-U_C. Кут зсуву фаз визначається із співвідношення

Отже, якщо X_L>X_C,, то кут зсуву фаз >0, якщо X_L<X_C, то <0, i якщо X_L=X_C, то =0. У колі має місце резонанс напруг.

У

колі однофазного змінного струму з послідовно з’єднаними активним R_L, iндуктивним X_L, i ємнісним X_C опорами (рис. 3 - вимикачі В1 i В2 розімкнуто, реостат R1 виведено) при умові, коли настала рівність між індуктивним і ємнісним опорами (X_L=X_C), виникає резонанс напруг. При резонансі , =0 тобто зсуву фаз між напругою і струмом немає, cos=cos0=1 (S=UIcos=P), повний опір у цьому разі , струм у колі I=U/R_L досягає максимального значення і називається резонансним.

Отже, таке коло має властивості кола з активним опором. Проте явища, що відбуваються в ньому, відрізняються від процесів, які мають місце у колі з активним опором.

Реактивні опори Х_L i Х_C не впливають на величину струму в колі, і їх величини Х_L=Х_C0. Спади напруг на цих опорах U_L i U_C також не дорівнюють нулю, вони зсунуті за фазою на половину періоду і взаємно компенсують одна одну.

Діючі значення цих напруг U_L i U_C називають резонансними напругами.

У колі, для якого Х_L=X_C>R, ці напруги більші від прикладеної напруги U у стільки разів, у скільки реактивний опір Х_L або Х_C більший від активного опору R, такі напруги можуть бути небезпечними для технічних установок.

Р

еактивна складова потужності у колі дорівнює нулю, але на ділянках з опорами Х_L i Х_C вона не дорівнює нулю. Реактивні потужності Q_L=I²X_L=I²X_C=Q_C0 пульсують з подвоєною частотою, протилежні за фазою (рис. 7) і обмінюються місцями на дільниці кола. Обміну потужності між котушкою і мережею (генератором), а також між конденсатором і мережею живлення не буде.

Отже, дільниця кола з Х_L i Х_C утворює коливальний контур, в якому відбувається обмін енергією; резонансну частоту можна знайти з рівності Х_L=Х_C, виразивши значення Х_L i Х_C в через індуктивність, ємність і частоту f₀, тобто 2f₀L=(2f₀C)^-1, звідки .

Ця частота, називається власною, або резонансною, частотою коливального контура.

Резонанс у колі настає тоді, коли власна частота контура збігається з частотою струму живлення (частотою вимушених коливань). В електричному колі з послідовно з’єднаними індуктивним і ємнісним опорами резонанс характеризується: зменшенням кута зсуву фаз між напругою і струмом у колі до нуля, зменшенням повного опору Z до найменшої величини, яка дорівнює активному опорові цього кола R, збільшенням струму у колі до максимального значення I=U/R, збільшенням напруги на дільницях кола з індуктивним і ємнісним опорами (U_L i U_C).

Явище резонансу напруг не допускають у колах силових струмів, у деяких випадках використовують у лініях електропередач й широко застосовують у радіотехніці.