Lektsii / 03 Силы Покой Давление

03-3

Силы, действующие в жидкостях: массовые и поверхностные.

Общие понятия о нормальных и касательных напряжениях.

Абсолютный и относительный покой (равновесие) жидкостей.

Гидростатическое давление в точке и его свойства.

Единицы измерения давления.

Силы, действующие на жидкость

К покоящейся жидкости не могут быть приложены сосредоточенные силы, а только распределенные по объему(массовые) или по поверхности (поверхностные).

Массовые силы:

Плотность распределения массовой силы есть сила, отнесенная к массе.

	Сила тяжести – обусловлена Земным притяжением На элементарную массу действует сила . Плотность распределения силы (ускорение свободного падения).
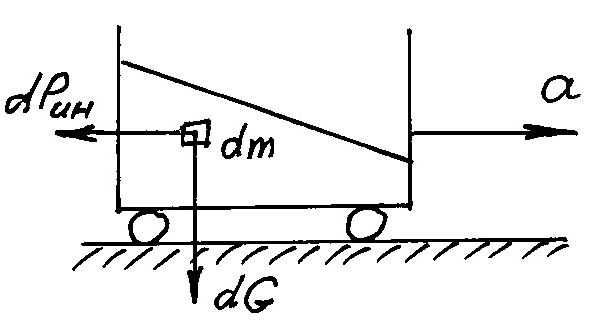
	Сила инерции – обусловлена движением с ускорением . . Плотность распределения силы инерции (ускорение). Направление скорости безразлично.
	Центробежная сила – обусловлена движением с ускорением при вращении. (фактически сила инерции) , где – угловая скорость вращения; – радиус, на котором находится масса ; – линейная скорость. Плотность распределения центробежной силы (ускорение)

Поверхностные силы

Силы, действующие на каждый элемент поверхностей, ограничивающих жидкость, и на каждый элемент поверхностей, проведенных произвольно внутри жидкости, называют поверхностными.

Сила , действующая на площадку площадью , представляется как сумма силы нормального напряжения и силы касательного напряжения .

Плотность распределения поверхностной силы есть сила, отнесенная к площади действия.

Плотность распределения нормальных сил называют нормальным напряжением (давлением). Плотность распределения касательных сил называют касательным напряжением.

Массовые и поверхностные силы могут быть внешними и внутренними.

Внешние силы действуют на рассматриваемую массу и поверхность жидкости извне и приложены соответственно к каждой частице жидкости, составляющей массу, и к каждому элементу поверхности, ограничивающей жидкость. Внутренние силы представляют собой взаимодействие частиц жидкости. Они являются парными, их сумма в данном объеме жидкости всегда равна нулю.

ГИДРОСТАТИКА

Гидростатика – раздел гидравлики, изучающий законы равновесия жидкостей в состоянии покоя.

Абсолютный покой – все частицы жидкости неподвижны относительно Земли (в общем случае – относительно неинерциальной системы отсчета)

Относительный покой – частицы жидкости неподвижны по отношению к резервуару, который движется с ускорением относительно Земли.

Нормальное напряжение – плотность распределения нормальных сил .

Это нормальное усилие отнесенное к величине этой площади. Нормальное напряжение – вектор.

Свойства нормального напряжения

1. Нормальное напряжение действует по внутренней нормали к пощади действия (является сжимающим напряжением).

Доказательство. Покажем, что сила действует по внутренней нормали к площадке . Доказательство от противного. а) Если бы сила была направлена не по нормали, то ее можно было бы разложить на нормальную и касательную составляющие. Из-за текучести жидкости касательная составляющая привела бы жидкость в движение, т.е. в этом случае равновесие жидкости было бы невозможно. Значит сила направлена по нормали. б) Так как жидкость не сопротивляется растягивающим напряжениям, то сила может быть только сжимающей.

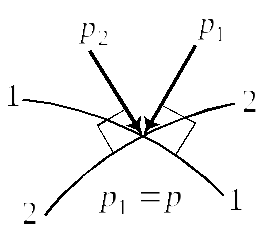
2. В покоящейся жидкости значение (модуль) нормального напряжения не зависит от ориентации площадки.

Доказательство.

Выделим в покоящейся жидкости элементарную частицу в форме тетраэдра с ребрами , , , выбранными вдоль координатных осей. Площадь основания , высота , объем (одна треть площади основания на высоту) .

Отбросим окружающую тетраэдр жидкость и для сохранения равновесия приложим к каждой грани тетраэдра поверхностные силы , , по направлениям осей и , действующую на наклонную грань по направлению нормали к ней . Кроме поверхностных на жидкость, заключенную в тетраэдре, действует массовая сила, проекции плотности распределения которой на оси координат обозначим , , .

Массовая сила равна произведению массы на плотность распределения силы. В направлении оси действует массовая сила .

Уравнение равновесия жидкости, заключенной в тетраэдре (сумма сил равна нулю), в проекции на ось :

, здесь –угол между нормалью к наклонной грани и осью координат.

Разделим обе части уравнения на площадь грани, перпендикулярной оси :

Упростим, учитывая что

. Стягиваем тетраэдр в точку, второе слагаемое обращается в 0, имеем: . Проекции уравнения равновесия на другие оси приведут к выводам:

и .

Следовательно . Таким образом доказано, что величина нормального напряжения в любой точке покоящейся жидкости не зависит от направления действия.

Это позволяет характеризовать напряженное состояние покоящейся жидкости в каждой точке скалярной величиной, представляющей значение нормального напряжения в этой точке и называемой гидростатическое давление (в дальнейшем слово «гидростатическое» опускается).

Давление может быть неодинаковым в разных точках покоящейся жидкости: .

Единицы измерения давления:

=Па (Паскаль) 1 кПа=10³Па; 1 МПа=10⁶ Па; 1 бар=10⁵ Па

=

Единицы столба жидкости (мм рт.ст; м вод.ст.)