
- •Редактор Е.Г.Козвонина
- •Введение
- •ГЛАВА 1 Классический метод расчёта переходных процессов
- •1.1. Определение переходного процесса
- •1.2. Законы коммутации
- •1.3. Переходный, принуждённый и свободный процессы
- •1.4. Порядок расчёта переходного процесса
- •1.5. Включение RL–цепи на постоянное напряжение
- •1.7. Короткое замыкание RL-цепи
- •1.8. Перенапряжение. Искровой разряд
- •1.9. Включение RC-цепи на постоянное напряжение
- •1.10. Короткое замыкание RC-цепи
- •1.11. Включение RL-цепи на синусоидальное напряжение
- •1.12. Включение RC-цепи на синусоидальное напряжение
- •1.13. Включение RLC-цепи на постоянное напряжение
- •ГЛАВА 2 Расчёт переходных процессов операторным методом
- •2.1. Преобразование Лапласа и его свойства
- •2.3. Законы Ома и Кирхгофа в операторной форме
- •2.6. Связь между преобразованиями Лапласа и Фурье
- •3.2. Переходные функции цепи. Импульсная переходная функция
- •3.3. Расчёт переходных процессов с помощью интеграла Дюамеля
- •4.1. Пассивные дифференцирующие цепи
- •4.2. Пассивные интегрирующие цепи
- •5.4. Основные рекомендации по применению программы EWB-5.12
- •Библиографический список

10
ГЛАВА 2 Расчёт переходных процессов операторным методом
2.1. Преобразование Лапласа и его свойства
Основой операторного метода является интегральное преобразование Лапласа
∞ |
|
F( p) = ∫ f (t)e− pt dt , |
(2.1) |
0 |
|
где f (t) – вещественная функция времени (напряжение |
или ток), |
удовлетворяющая условиям Дирихле и равная нулю при t < 0, называемая оригиналом; F( p) – функция комплексной переменной (комплексной частоты) p = s + jω, называемая изображением по Лапласу.
Сокращённо формулу (2.1) (прямое преобразование Лапласа функции f (t) )
записывают в виде F( p) = L{f (t)}. Связь между f (t) и F( p) |
обозначают |
также, как f (t) F( p), где « » – знак соответствия. |
|
Что касается ограничений, налагаемых на f (t) условиями |
Дирихле, то |
реальные напряжения и токи им всегда удовлетворяют.
Найдём изображения для простейших функций времени (напряжений). 1. f (t) =U ;
|
∞ |
−pt |
|
|
|
1 |
|
−pt |
|
∞ |
|
U |
|
|
|
U |
|
||
|
|
|
|
|
|
|
|
|
|||||||||||
F( p) = |
∫ |
Ue |
|
dt =U |
− |
|
e |
|
|
|
= − |
|
(0 |
−1) |
= |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
p |
|
|
0 |
|
p |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом U |
U |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(2.2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. f (t) =Ue−β t ;
∞ |
U |
|
|
|
F( p) = ∫Ue−β te− pt dt = − |
|
e−( p+β)t |
||
p + |
β |
|||
0 |
|
3.f (t) =U (1−e−β t )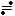 Up − pU+ β
Up − pU+ β
4.Ume jωt =Um cosωt + jUm sin ωt 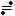
|
Um |
=Um |
p + jω |
= |
|
p − jω |
( p − jω)( p + jω) |
||
|
|
|
||
откуда |
|
|
|
|
|
|
∞ = |
U |
|
|
. |
|
|
(2.3) |
|||
|
|
|
|
|
|
|||||||
|
|
p + |
β |
|
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
= |
|
|
βU |
|
|
|
. |
|
|
(2.4) |
||
|
p( p + |
β) |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
Um p |
|
+ j |
Umω |
, |
(2.5) |
||||
|
|
p2 +ω2 |
|
p2 +ω2 |
||||||||
Um cosωt Um |
|
p |
|
; |
(2.6) |
|
p2 |
+ |
ω2 |
||||
|
|
|

11
|
Um sinωt Um |
|
ω |
|
. |
(2.7) |
|||
|
|
p2 +ω2 |
|||||||
|
|
|
ω |
|
|
|
|||
5. Ume−βt sinωt Um |
|
|
|
|
. |
|
(2.8) |
||
|
|
|
|
|
|
||||
( p + β)2 |
+ω2 |
|
|||||||
|
|
|
|
|
|||||
6. Ute−β t U |
1 |
|
. |
|
|
|
|
|
(2.9) |
( p + β)2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Подробные таблицы изображений функций приведены в [1,4,13]. Рассмотрим без вывода два важных свойства преобразования Лапласа.
1. Теорема дифференцирования. Изображение первой производной функции равно изображению функции, умноженному на p , минус значение функции при
t = 0.
L{f ′(t)}= ∞∫{f ′(t)}e− pt dt = pF( p) − f (0) . |
(2.10) |
||||||
|
0 |
f (0) = 0 , |
|
|
|
|
|
В частном случае, когда |
|
|
|
|
|||
|
′ |
|
|
|
|
|
(2.11) |
|
L{f (t)}= pF( p) . |
|
|
|
|||
2. Теорема интегрирования. Изображение интеграла функции равно |
|||||||
изображению этой функции, делённому на |
p . |
|
|
|
|||
L t |
f (t)dt |
= ∞ t f (t)dt |
e−pt dt = |
F( p) |
. |
(2.12) |
|
|
|||||||
∫ |
|
∫ |
∫ |
|
p |
|
|
0 |
|
0 |
0 |
|
|
||
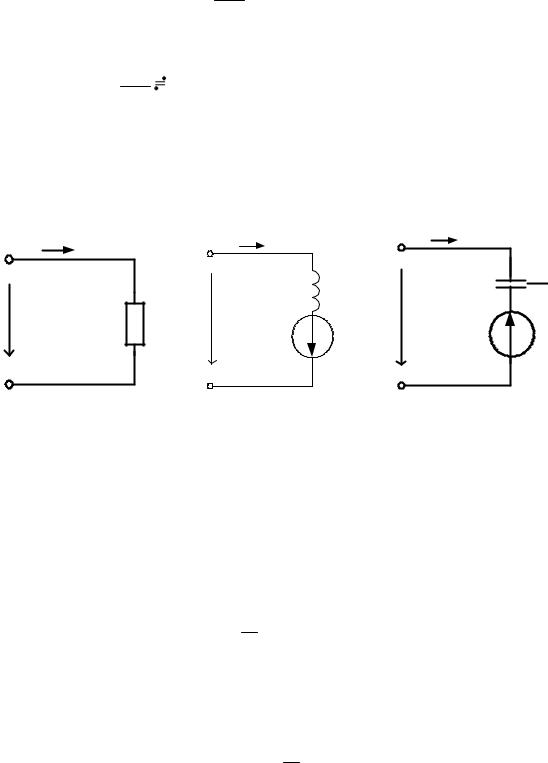
2.2. Изображения по Лапласу напряжений на резисторе, индуктивности и ёмкости
Найдём изображения напряжений для простейших цепей |
(рис. 2.1 |
а, б, в), используя обозначения: |
|
u U ( p); i I ( p) . |
|
iR |
iL |
iC |
uR |
R |
uL |
L |
uC |
C |
а |
б |
в |
Рис. 2.1
12
В цепи на рис. 2.1 а мгновенные напряжение и ток связаны законом Ома uR = RiR ,
и изображение имеет вид |
U R ( p) = RIR ( p). |
(2.13) |
||||
|
|
|||||
Операторная схема замещения цепи рис. 2.1 а показана на рис. 2.2 а. |
|
|
||||
Для схемы на рис. 2.1 б |
= L diL . |
|
|
|
||
|
uL |
|
(2.14) |
|||
|
|
dt |
|
|
|
|
Используя теорему дифференцирования (2.10), получим формулу для uL |
|
|||||
uL |
= L diL |
pLIL ( p) − LiL (0−) =U L ( p) . |
(2.15) |
|||
|
dt |
|
|
|
|
|
Если iL (0−) = 0 , то |
|
|
|
|
|
|
|
U L ( p) = pLIL ( p) . |
|
|
|
||
На рис. 2.2 б изображена операторная схема замещения, соответствующая |
||||||
формуле (2.15). |
|
|
|
IC (p) |
|
|
IR (p) |
|
|
IL (p) |
|
|
|
|
|
|
|
|
||
|
|
|
p |
|
1 |
|
|
|
|
L |
|
p |
|
|
|
|
UC (p) |
C |
|
|
UR(p) |
|
U L (p) |
|
|||
R |
( |
) |
||||
|
|
|
|
Li (0− ) |
uC 0− |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
а |
|
б |
|
в |
|
|
|
|
Рис. 2.2 |
|
|
|
|
Операторная ЭДС LiL (0−) , называемая внутренней, учитывает ток через |
||||||
индуктивность при |
t = 0 (ненулевое |
начальное |
условие) и определяется для |
|||
момента t = 0− , предшествующего |
коммутации |
в цепи. Направление |
ЭДС |
|||
LiL (0−) совпадает с выбранным направлением тока IL ( p) . |
|
|
||||
Напряжение на ёмкости (рис. 2.1 в) находится по формуле |
|
|
||||
uC = C1 ∫iC dt .
В этой формуле не указаны пределы интегрирования. Если учесть, что до коммутации ёмкость была заряжена до напряжения uC (0−), то мгновенное
напряжение на ёмкости в момент времени t примет вид
uC = uC (0−) + 1 ∫t iC dt . C 0
13
В соответствии с формулами (2.2) и (2.12):
u |
|
(0 |
|
) |
uC (0 |
−) |
и |
1 |
t |
i dt |
IC ( p) |
. |
C |
− |
|
|
|
∫ |
|
||||||
|
|
|
p |
|
|
|
C |
pC |
||||
|
|
|
|
|
|
|
C 0 |
|
||||
В итоге получим изображение для напряжения на ёмкости и операторную схему замещения (рис. 2.2 в).
|
|
u |
|
= u |
|
(0 |
|
) + |
1 t |
i dt |
uC (0−) |
+ |
IC ( p) |
=U |
|
( p) , |
(2.16) |
|||||||
|
|
C |
C |
− |
|
∫ |
|
|
|
|
|
C |
||||||||||||
|
|
|
|
|
|
|
|
C |
|
p |
|
|
pC |
|
|
|||||||||
|
uC (0 |
−) |
|
|
|
|
|
|
C 0 |
|
|
|
|
|
|
|
||||||||
где |
– внутренняя ЭДС. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В частном случае при uC (0−) = 0 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
UC ( p) = |
IC ( p) |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pC |
|
|
|
|
|
|
|
||
|
Отметим, что внутренняя ЭДС |
|
uC (0−) |
|
(рис. 2.2 в) направлена встречно |
|||||||||||||||||||
|
|
p |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
выбранному направлению тока IC ( p).
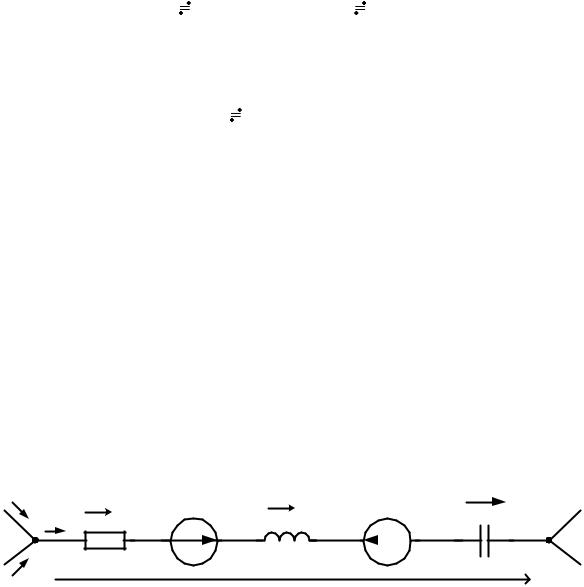
2.3. Законы Ома и Кирхгофа в операторной форме
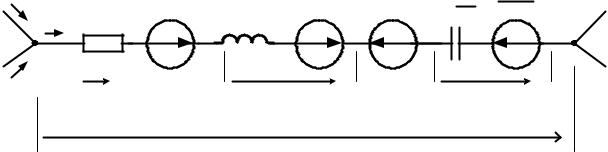
На рис. 2.3 изображена ветвь разветвлённой электрической цепи, в которой происходит коммутация.
i1 |
uR |
e1 |
u |
L |
e2 |
uC |
|
|
C |
|
|||||
i |
R1 |
|
L |
|
+ - |
b |
|
a |
|
|
|
|
|
||
i |
|
|
uab |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.3 |
|
|
uab , |
|
Выберем |
условно |
положительное |
направление |
напряжения |
|||
приложенного к концам ветви ab , и согласованное с ним направление тока i . Положим также, что к моменту коммутации в ветви протекал ток i(0−), а
начальное напряжение на ёмкости равнялось uC (0−). Переходя к изображениям
(2.13), (2.15), (2.16) и используя схемы (рис. 2.2), составим операторную схему замещения для ветви ab (рис. 2.4).
14
I1 |
(p) |
|
(p) |
|
Li (0− ) |
E2(p) |
1 |
uC(0− ) |
|
E1 |
p |
p |
|||||||
|
I (p) |
p |
|||||||
a |
R |
|
L |
|
|
C |
b |
||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
I 2(p) |
UR(p) |
|
|
U L(p) |
|
UC (p) |
|||
|
|
|
|
||||||
|
|
|
|
|
U a (p) |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
Рис. 2.4 |
|
|
|
|
U |
ab |
( p) |
= RI ( p) − E |
( p) + pLI ( p) − Li(0 |
− |
) |
+ E |
2 |
( p) + |
1 |
I |
( p) + |
uC (0−) |
= |
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pC |
|
|
|
|
|
|
|
p |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
C |
(0 |
− |
) |
|
||
|
|
|
|
= R + pL |
+ |
|
I ( p) |
− E ( p) − Li(0 |
− |
) + E |
2 |
( p) |
+ |
|
|
|
|
|
. (2.17) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
pC |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Из уравнения (2.17) получаем изображение тока |
|
I ( p) |
|
в ветви ab , которое |
||||||||||||||||||||||||||||||||||
называется обобщённым законом Ома в операторной форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
U |
ab |
( p) |
+ E ( p) + Li(0 |
− |
) − E |
2 |
( p) − |
uC (0−) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
I ( p) = |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(2.18) |
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Z( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
Z ( p) = R + pL + |
|
|
– операторное сопротивление ветви |
ab ; |
Li(0−) и |
|||||||||||||||||||||||||||||||||||
|
pC |
||||||||||||||||||||||||||||||||||||||||
|
uC (0−) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
– внутренние ЭДС, учитывающие ненулевые начальные условия для L и |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
ab отсутствуют внешние и внутренние |
|||||||||||||||||||||||||||||
|
|
|
В частном случае, когда в ветви |
||||||||||||||||||||||||||||||||||||||
ЭДС, т.е. E ( p) = 0 |
и E2 |
(p) =0; i(0 |
− |
) = 0 и u |
C |
(0 |
− |
) = 0 (начальные условия |
|||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нулевые), закон Ома имеет вид |
|
|
|
|
Uab ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
I ( p) = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.19) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Закон Ома применяется для отдельной ветви, а также для одноконтурной замкнутой цепи, не имеющей разветвлений.
Законы Кирхгофа в операторной форме используются для расчёта переходных процессов в разветвлённых электрических цепях, содержащих две и более ЭДС (внутренних и внешних) в разных ветвях цепи.
Прежде всего для цепи составляют операторную схему замещения, на которой задают направления токов в ветвях и направления обхода контуров.
П е р в ы й з а к о н К и р х г о ф а. Алгебраическая сумма изображений токов, сходящихся в любом узле разветвлённой цепи, равна нулю.
15
n
I1( p) + I2 ( p) +L+ In ( p) = ∑Ik ( p) = 0. (2.20)
k =1
Токи, направленные к узлу, будем условно считать положительными, а токи, направленные от узла, – отрицательными.
В т о р о й з а к о н К и р х г о ф а. В любом замкнутом контуре разветвлённой электрической цепи алгебраическая сумма изображений напряжений равна алгебраической сумме изображений ЭДС.
|
|
|
|
u |
Ck |
(0 |
− |
) |
|
|
∑Zk ( p)Ik ( p) = ∑ Ek ( p) + Lk ik (0 |
− ) − |
|
|
|
. |
(2.21) |
||||
|
|
p |
|
|
||||||
k |
k |
|
|
|
|
|
|
|
|
|
Знаки слагаемых в выражении (2.21) положительные, если направления токов и ЭДС в ветвях совпадают с направлением обхода контура, и отрицательные, если не совпадают.
При нулевых начальных условиях: ik (0−) = 0, uCk (0−) = 0 |
|
|
∑Zk ( p)Ik ( p) = ∑Ek ( p). |
(2.22) |
|
k |
k |
|
Для расчёта переходных процессов операторным методом можно использовать любые методы расчёта цепей постоянного тока, вытекающие из уравнений Кирхгофа (контурных токов, узловых потенциалов, эквивалентного генератора, наложения), предварительно составив для заданной цепи операторную схему замещения. Выбор метода расчёта, как известно, зависит от конфигурации цепи и имеет целью уменьшить объём вычислений.
2.4. Порядок расчёта переходных процессов операторным методом. Переход от изображений к оригиналам
Расчёт операторным методом ведётся в следующей последовательности: 2.1. В исходной цепи до коммутации определяются независимые
начальные условия: iL (0−) и uC (0−).
2.1.Составляется операторная схема замещения цепи после коммутации,
на |
которой |
все ЭДС, |
напряжения и токи заменяются их изображениями |
||||
[e |
E( p),u |
U ( p),i |
I(p)]; |
индуктивности |
и |
ёмкости |
заменяются |
операторными схемами с внутренними ЭДС (рис. 2.2 а, б). Ключ на схеме не показывают.
2.1. Определяются изображения искомых токов и напряжений любым, подходящим для составленной схемы методом расчёта цепей постоянного тока.
2.1. Осуществляется обратный переход от изображений к оригиналам (функциям времени) либо с помощью таблиц изображений функций (формул соответствия), например (2.2)–(2.9), либо с использованием теоремы разложения.
Т е о р е м а р а з л о ж е н и я. Если изображение тока (или напряжения) имеет вид рациональной дроби
16
|
|
a pm +a |
pm−1 |
+L+a p |
+a |
F (p) |
|
||||||||||||
I(p) = |
m |
m−1 |
|
|
|
|
1 |
|
|
|
0 |
|
|
1 |
|
|
|||
p(b pn +b |
|
pn−1 |
|
|
+b )= |
|
, |
(2.23) |
|||||||||||
|
+L+b p |
pF2(p) |
|||||||||||||||||
|
|
n |
n−1 |
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|||
причём m < n; a |
k |
и b – вещественные числа; дробь |
|
F1( p) |
несократимая, т.е. |
||||||||||||||
|
|
||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
pF2 ( p) |
|
|
|
||||
многочлены F1( p) и F2 ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
не имеют общих корней, |
то оригинал находится по |
||||||||||||||||||
формуле |
|
|
F1(0) |
|
|
n |
F1( pk ) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
e pk t , |
|
|
|
|
|
|
||||||||
|
|
i = |
+ ∑ |
|
|
|
|
|
|
(2.24) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
где pk – |
|
|
F2 (0) |
|
k =1 pk F2′( pk ) |
|
|
|
|
|
|
|
|
||||||
различные |
и |
|
не |
|
равные |
нулю |
корни |
уравнения |
|||||||||||
|
|
|
|
|
|
|
|
|
|
dF2 ( p) |
|
|
|
|
|
|
|
||
F2 ( p) = 0 (k =1,2...n) ; |
F2′( pk ) = |
|
|
|
|
|
|
|
|||||||||||
dp |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
p=pk . |
|
|
|
|
|||||||||
Если в знаменателе выражения (2.23) |
нет множителя p (отсутствует |
|||||||||
нулевой корень), то формула разложения (2.24) принимает более простой вид |
||||||||||
|
F (p) |
n |
F |
(p ) |
epkt |
|
|
|||
|
1 |
|
i = ∑ |
1 |
|
k |
|
. |
(2.25) |
|
|
|
′ |
|
|
||||||
F (p) |
|
|||||||||
|
= |
(pk ) |
||||||||
2 |
|
k 1F2 |
|
|
|
|||||
Заметим, что уравнение |
F2 ( p) = 0 |
совпадает |
с характеристическим |
|||||||
уравнением цепи, а наличие нулевого корня в выражении (2.23) свидетельствует о том, что оригинал – переходный ток (напряжение) содержит принуждённую
составляющую, равную F1(0) .
F2 (0)
Если уравнение F2 ( p) = 0 содержит комплексно-сопряжённые корни pk и pk , то достаточно определить слагаемое сумм в формулах (2.24) или (2.25)
только для одного корня pk , а для корня pk взять значение, сопряжённое этому слагаемому. Тогда сумма этих слагаемых будет равна удвоенному значению вещественной части, найденной для корня pk .
Когда среди корней уравнения F2 ( p) = 0 есть несколько одинаковых
(кратных) корней, формула разложения усложняется. В этом случае рекомендуется пользоваться таблицами изображений функций по Лапласу. В
частности, если уравнение F2 ( p) = 0 в (2.25) имеет два равных корня p1,2 = −β , то определить оригинал можно по формуле (2.9).
В большинстве практических задач использование формул разложения (2.24), (2.25) является основным способом перехода от изображений к оригиналам.
17
В тех случаях, когда требуется найти только начальное и установившееся значения тока, т.е. i(0+) и i(∞) , то, не прибегая к вычислениям по формулам (2.24), (2.25), можно использовать следующие предельные соотношения:
i(0+)=lim pI(p) |
(2.26) |
p→∞ |
и |
i(∞)=lim pI(p) |
. |
(2.27) |
p→0 |
Формулы (2.26) и (2.27) позволяют просто определить i(0+) и i(∞) , если
установившийся процесс непериодический, и могут быть использованы также для контроля за правильностью вычислений на стадии получения изображений.
2.5. Применение операторного метода к исследованию электрических цепей
На основе изложенного в §§ 2.1 – 2.3 можно сделать вывод, что использование преобразования Лапласа позволяет упростить исходные функции времени, и особенно операции дифференцирования и интегрирования. В результате решение интегро-дифференциальных уравнений относительно оригиналов сводится к решению алгебраических уравнений относительно их изображений.
Отметим аналогию между операторным методом и комплексным методом расчёта цепей синусоидального тока. В обоих случаях операции над функциями времени заменяются операциями над их символами (либо изображениями по Лапласу, либо комплексными числами). Законы Ома, Кирхгофа в операторной форме (2.18), (2.19), (2.21), (2.22) аналогичны по форме записи тем же законам в комплексной форме, а операторное сопротивление цепи Z ( p) совпадает с
комплексным Z при замене p на jω.
Если сравнивать классический и операторный методы, то следует заметить, что первый позволяет проще интерпретировать переходный процесс с физической точки зрения, тогда как операторный, подобно другим символическим методам, является сугубо формальным.
Как показывает опыт, расчёт переходных процессов в цепях первого и второго порядка классическим методом, как правило, проще, чем операторным. В цепях более высокого порядка из-за трудностей, возникающих при нахождении постоянных интегрирования в классическом методе, более рациональным является операторный метод. Последний широко применяется также в том случае, когда к цепи приложена внешняя ЭДС сложной формы (отличной от постоянной и синусоидальной), так как упрощается определение принуждённой составляющей переходного тока (напряжения).
