
- •Редактор Е.Г.Козвонина
- •Введение
- •ГЛАВА 1 Классический метод расчёта переходных процессов
- •1.1. Определение переходного процесса
- •1.2. Законы коммутации
- •1.3. Переходный, принуждённый и свободный процессы
- •1.4. Порядок расчёта переходного процесса
- •1.5. Включение RL–цепи на постоянное напряжение
- •1.7. Короткое замыкание RL-цепи
- •1.8. Перенапряжение. Искровой разряд
- •1.9. Включение RC-цепи на постоянное напряжение
- •1.10. Короткое замыкание RC-цепи
- •1.11. Включение RL-цепи на синусоидальное напряжение
- •1.12. Включение RC-цепи на синусоидальное напряжение
- •1.13. Включение RLC-цепи на постоянное напряжение
- •ГЛАВА 2 Расчёт переходных процессов операторным методом
- •2.1. Преобразование Лапласа и его свойства
- •2.3. Законы Ома и Кирхгофа в операторной форме
- •2.6. Связь между преобразованиями Лапласа и Фурье
- •3.2. Переходные функции цепи. Импульсная переходная функция
- •3.3. Расчёт переходных процессов с помощью интеграла Дюамеля
- •4.1. Пассивные дифференцирующие цепи
- •4.2. Пассивные интегрирующие цепи
- •5.4. Основные рекомендации по применению программы EWB-5.12
- •Библиографический список
21
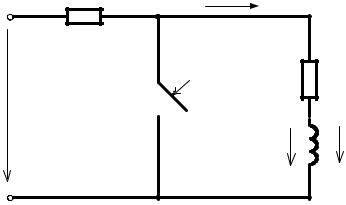
1.7. Короткое замыкание RL-цепи
|
R1 |
i |
|
|
+ |
|
|
|
|
U |
t = 0 |
|
R |
|
S |
|
|
|
|
|
|
e |
L |
uL |
|
|
|
|
-
Рис. 1.10
В цепи (рис. 1.10), к которой приложено постоянное напряжение U, в момент t=0 ключ S замыкает накоротко индуктивную катушку RL. Найти законы изменения тока в катушке, ЭДС самоиндукции и напряжения на индуктивности.
Переходный ток i = iпр +iсв .
В установившемся режиме после коммутации iпр = 0 и i = iсв . Свободный ток iсв =Ae pt - результат решения однородного дифференциального уравнения
L |
diсв |
+ Ri = 0, |
характеристическое |
уравнение |
которого Lp + R = 0 |
имеет |
|||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
dt |
св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корень p = − R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||
|
Постоянную |
|
интегрирования |
|
|
|
|
найдём, |
используя первый |
закон |
|||||||||||||||||
коммутации: i(0− ) = i(0+ ) = |
|
|
U |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
R1 + R |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
U |
|
= Ae− |
R |
0 , откуда A = |
|
|
U |
|
|
|||||||||||||
|
Для t = 0 |
|
|
L |
|
|
. |
|
|||||||||||||||||||
|
+ R |
|
+ R |
|
R + R |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
Таким образом, ток в цепи после коммутации |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
R |
|
|
U |
|
e− |
t |
|
|
|
||||
|
|
|
|
i = iсв |
= |
|
|
e− |
|
t |
= |
|
|
, |
|
(1.24) |
|||||||||||
|
|
|
|
|
|
L |
|
τ |
|
||||||||||||||||||
|
|
|
|
R1 + R |
|
R1 + R |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
22 |
|
|
|
|
|
|
|
||
U |
i |
|
|
|
|
|
|
|
|
|
|
|
|
R1 +R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
= i св |
= |
|
U |
|
e |
−t |
τ |
|
|
||
|
|
R 1 |
+ R |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
L |
|
|
|
|
|
|
|
|
3 τ |
t |
|
τ |
= |
R |
|
|
|
|
|
2 τ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t пп = |
3 τ |
|
|
|
|
|
||||
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
uL |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e = |
|
|
R |
|
U −t τ |
|
|
|
|||
|
|
R |
|
+ R e |
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
2τ |
|
3τ |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
uL = − |
|
R |
|
U −t τ |
|
|
|
||||
|
|
|
|
|
R + R e |
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
||
|
|
|
|
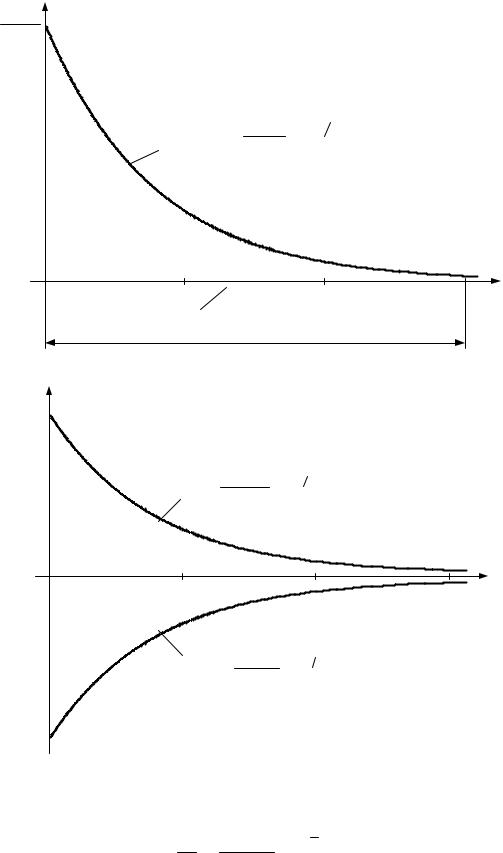
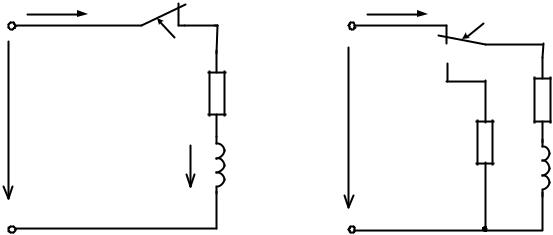
Рис. 1.11 |
|
|
|
|
|
||||
ЭДС самоиндукции e = −L di |
|
|
|
R |
|
Ue− |
t |
|
|
|
|||
= |
R |
|
|
τ , |
|
|
(1.25) |
||||||
|
|
dt |
|
|
+ R |
|
|
|
|
|
|
||
напряжение на индуктивности |
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
23
uL = −e = L |
di |
|
R |
Ue− |
t |
|
|
|
= − |
τ . |
(1.26) |
||||||
dt |
R1 + R |
|||||||
|
|
|
|
|
|
|||
С энергетической точки зрения переходный процесс в цепи состоит в том, что энергия, накопленная к моменту коммутации в магнитном поле катушки, во время переходного процесса рассеивается в виде тепла на активном сопротивлении R. На рис. 1.11 изображены кривые, построенные по формулам
(1.24) – (1.26).
1.8. Перенапряжение. Искровой разряд
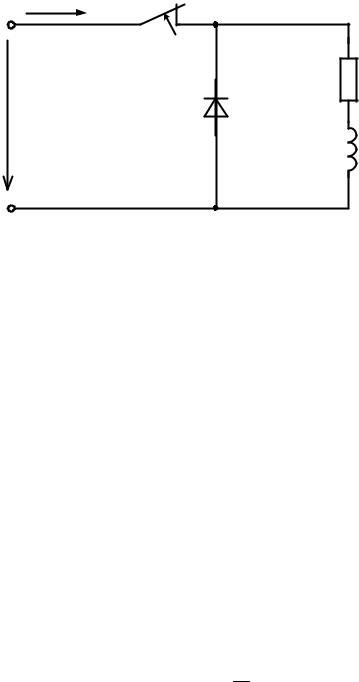
При размыкании цепи, содержащей индуктивную катушку (рис. 1.12 а),
ток резко уменьшается и ЭДС самоиндукции e = −L dtdi может быть весьма
значительной. На контактах, разрывающих цепь, появляется перенапряжение, равное сумме напряжения питания и ЭДС самоиндукции. При напряжении около 300 В между расходящимися контактами возникает искровой разряд (электрическая дуга).
Перенапряжение на индуктивной катушке и сопровождающая его искра на контактах – нежелательные явления, которые необходимо иметь в виду при разработке схем, содержащих катушки с большой индуктивностью.
Перенапряжение может вызвать пробой изоляции; искрение приводит к эрозии, обгоранию контактов и сокращает срок их службы. Кроме того,
i |
S |
|
i |
t = 0 |
+ |
|
|
+ |
|
t =0 |
|
S |
||
|
|
|
||
U |
|
R |
U |
R |
|
|
|
||
|
e |
|
|
Rp |
|
L |
|
L |
|
|
|
|
||
- |
|
|
- |
|
|
а |
|
|
б |
|
|
24 |
+ |
i |
S |
|
|
t =0 |
|
|
R |
U |
|
VD |
|
|
L |
-
в
Рис. 1.12
искровой разряд между контактами является одной из причин импульсных помех
врадио- и проводных линиях связи.
Вчастности, интенсивные радиопомехи создают коллекторные электрические машины. Это объясняется резкими изменениями тока при переходе щёток с одной коллекторной пластины на другую и сопутствующему этому процессу искрению.
Снижение перенапряжений и искрогашение осуществляют с помощью специальных схем, не допускающих резких изменений тока в цепи с индуктивностью. Например, обмотку возбуждения (рис. 1.12 б) мощной электрической машины (при необходимости снять возбуждение) замыкают на
разрядное сопротивление Rp . Подобным образом поступают при динамическом
торможении двигателя постоянного тока, шунтируя обмотку якоря сопротивлением.
В маломощных цепях параллельно с индуктивной катушкой включают диод (рис. 1.12 в). Если в качестве ключа S используют транзистор, то при его запирании (размыкании ключа) диод защитит транзистор от пробоя.
Заметим, что схемы на рис. 1.12 б, в замедляют затухание тока в цепи.
Время переходного процесса tПП = 3τ = 3 RL будет тем меньше, чем больше сопротивление R контура.
1.9. Включение RC-цепи на постоянное напряжение
Известны напряжение U , параметры цепи R и C ; напряжение uC (0− ) = 0. Найти ток i и напряжения uR и uC после коммутации.

|
|
|
|
25 |
|
|
i |
S |
t = 0 |
R |
|
+ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
uR |
С |
U |
|
|
|
|
|
|
|
|
|
uC |
-
Рис. 1.13
Уравнение равновесия напряжений для контура на рис. 1.13 имеет вид
Ri+uc =U.
Выразив ток i через напряжение u |
C |
i = C |
duc |
, получим |
|
|||
dt |
|
|||||||
|
duc |
|
|
|
|
|||
RC |
+uc =U , (t > 0). |
(1.27) |
||||||
|
||||||||
|
dt |
|
|
|
|
|
||
Переходное напряжение на ёмкости |
|
|
|
|
||||
|
|
|
|
u =u |
+u |
=U+Ae pt. |
(1.28) |
|||||
|
|
|
|
c |
cпр |
cсв |
|
|
|
|
|
|
Характеристическое уравнение |
|
|
|
|
|
|
||||||
|
|
|
|
R + |
1 |
|
= 0 или RCp +1 = 0 |
|
|
|
|
|
|
|
|
|
Cp |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
имеет корень |
p |
= − |
1 |
, откуда |
постоянная времени |
цепи τ = |
|
1 |
= RC . |
|||
|
|
|
||||||||||
|
1 |
|
RC |
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя второй закон коммутации, находим независимое начальное условие
uC (0− ) = uC (0+ ) = 0
и постоянную интегрирования из формулы (1.28)
uC (0+ ) = 0 =U + Ae p 0 ; A = −U .
Окончательно
uC =U −Ue |
− t |
|
|
|
|
|
−e |
−t |
|
(1.29) |
|||
RC =U 1 |
|
τ . |
|||||||||||
Переходный ток в контуре |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
i = C |
du |
c |
|
U |
e |
− |
|
|
|
||||
= |
RC . |
|
(1.30) |
||||||||||
|
dt |
|
R |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Напряжение на активном сопротивлении
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
uR = Ri =Ue |
− t |
−t |
|
|
||||||
|
|
|
|
|
RC =Ue |
|
τ . |
(1.31) |
||||||
Закон изменения ёмкостного сопротивления в переходном режиме |
||||||||||||||
|
|
|
|
|
|
|
|
|
−t |
τ |
|
|
|
|
|
|
(t) = uc |
|
U 1−e |
|
|
|
|
|
|
||||
|
XC |
= |
|
|
|
|
|
= R(e tτ −1) . |
|
|||||
|
|
|
|
i |
|
|
U e−tτ |
|
|
|
|
|||
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
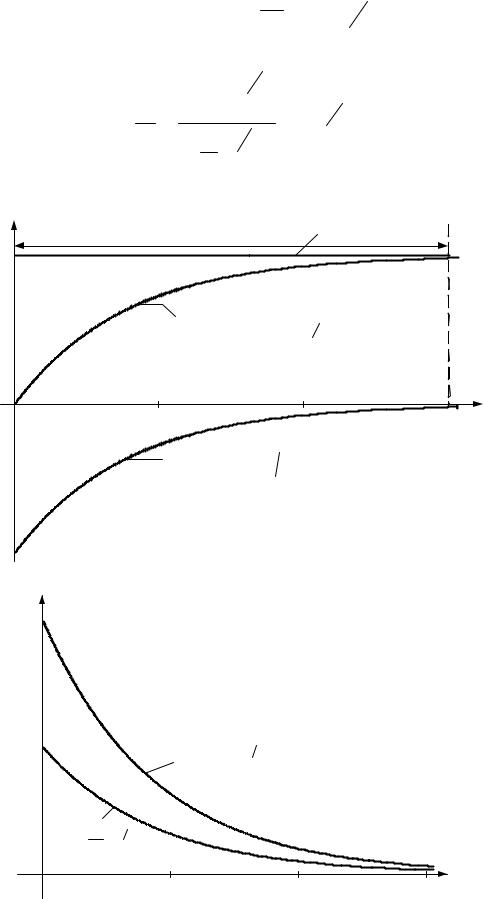
Графики uC , uR , i , Xc (t) представлены на рис. 1.14. |
|
|
||||||||||||
uc |
|
|
|
|
t пп=3 τ |
|
|
ucпр= U |
|
|||||
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
= u |
cпр |
+u |
=U(1−e −t τ) |
|
|
|
|||
|
|
|
|
c |
|
|
с в |
|
|
|
|
|
||
0 |
|
|
|
|
τ |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
τ |
||
|
|
|
|
|
|
|
|
|
|
|
2τ |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−t τ |
|
|
|
|
|
|
|
|
uCсв = −Ue |
|
|
|
||||||
uR |
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
uR = Ue −t |
τ |
|
|
|
||||
R |
|
|
|
|
|
|
|
|
||||||
|
i = |
U |
e |
−t τ |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
2τ |
|
3τ t |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.14 |
|
|
|
|||
