61
тора-столбца A. Эта система имеет ненулевое решение, если ее определитель равен нулю
det ( |
|
−ω2 |
|
)=0. |
(3.52) |
K |
M |
Левая часть уравнения (3.52) может быть представлена в виде полинома степени s относительно ω2, из которого определяются квадраты частот ω12 , ω22 ,..., ω2s. Их обычно располагают в порядке возрастания. Затем из уравне-
ния (3.51) для каждой частоты ωi можно определить форму колебаний Ai
(i=1,2,..., s). Таким образом, в рассматриваемой системе в результате определенных начальных возмущений могут происходить гармонические колебания с частотами ωi, каждой из которых соответствует своя форма колебаний Ai. Они
называются соответственно |
с о б с т в е н н ы м и ч а с т о т а м и и с о б - |
с т в е н н ы м и ф о р м а м и |
колебаний. Совокупность частоты и соответству- |
ющей ей формы колебаний называют т о н о м .
3.2.3. Системы с бесконечным числом степеней свободы
Колебания стержней
Для описания колебаний стержня используем континуальный подход (рис. 3.1а). Выше было получено дифференциальное уравнение поперечных колебаний прямолинейного стержня переменного сечения (3.32). Перепишем это уравнение в следующем виде
∂2 |
(EI z |
∂2 v |
)+mx |
∂2 v |
=q( x , t). |
(3.53) |
∂ x2 |
∂ x2 |
∂t2 |
Решение уравнения (3.53) должно удовлетворять граничным и начальным условиям.
Рассмотрим свободные колебания стержней, т.е. когда внешняя нагрузка отсутствует q( x , t)=0
∂∂x22 (EI z ∂∂2xv2 )+mx ∂∂2tv2 =0.
Это уравнение является однородным, оно допускает решения вида v ( x, t)=V ( x)sin ωt,
где V (x) – неизвестная форма колебаний;
ω – неизвестная круговая частота колебаний. Подставив решение (3.55) в уравнение (3.54), получим
d 2 (EI z d 2 V )−ω2 mx V =0. dx2 dx2
(3.54)
(3.55)
(3.56)
|
|
62 |
|
|
|
Уравнение (3.56) является однородным дифференциальным уравнением |
|||
четвертого порядка с неизвестным параметром ω. Общее решение этого уравне- |
||||
ния складывается из четырех линейно независимых решений с неизвестными |
||||
коэффициентами (произвольными константами). Подстановка этого решения в |
||||
граничные условия на концах стержня приводит к системе четырех линейных |
||||
однородных алгебраических уравнений относительно четырех неизвестных ко- |
||||
эффициентов. Эта система имеет ненулевое решение, когда ее определитель ра- |
||||
вен нулю. Приравнивая нулю определитель системы, получим частотное урав- |
||||
нение в виде трансцендентного уравнения, зависящего от круговой частоты ω. |
||||
Это уравнение имеет бесчисленное множество корней ω1 ,ω2 , ...,ωn , ..., которые |
||||
являются собственными частотами. Для каждой частоты ωn затем определяются |
||||
четыре произвольные константы и находится соответствующая форма колеба- |
||||
ний V n (x), n=1,2,.... Так как задача однородная, то каждая форма колебаний |
||||
определяется с точностью до произвольной константы. То есть данный метод |
||||
не позволяет определить реальные перемещения точек стержня при колебани- |
||||
ях, а позволяет определить только его форму. |
|
|
||
|
Рассмотрим для примера собственные колебания стержня постоянного се- |
|||
чения |
(EI z=const, mx=const). В этом случае |
дифференциальное |
уравнение |
|
(3.56) принимает вид |
|
|
|
|
|
d 4 V |
−k4 V =0, |
|
(3.57) |
|
dx4 |
|
|
|
где |
k4=ω2 mx . |
|
|
(3.58) |
|
EI z |
|
|
|
|
Общее решение уравнения (3.57) можно представить в виде |
|
||
|
V (x)=C1 sin kx+C 2 cos kx+C3 sh kx+C4 ch kx, |
(3.59) |
||
где C1, C2, C3, C4 – произвольные константы. |
|
|
||
|
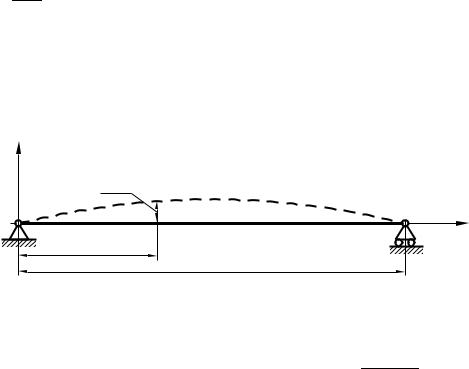
Пусть стержень по концам имеет шарнирное опирание (рис. 3.4). |
|||
|
y |
|
|
|
|
V(x) |
|
|
|
|
O |
|
x |
|
|
x |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
Рис. 3.4. Шарнирно опертый стержень |
|
||
Граничные условия для такого стержня были рассмотрены выше при ис-
следовании его устойчивости: V (0)=V (l )=0, d 2 V (0)= d 2 V (l)=0. dx2 dx2
63 Подставляя в эти граничные условия решение (3.59), получим систему
уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (0)=C1 sin k 0+C2 cos k 0+C3 sh k 0+C4 ch k 0=C 2+C 4=0; |
(3.60) |
|||||||||||||||||
|
|
|
V (l)=C1 sin kl +C2 cos kl +C 3 sh kl +C4 ch kl=0; |
|
|
(3.61) |
||||||||||||
d 2 V (0) |
=−C1 k |
2 |
sin k 0−C2 k |
2 |
cos k 0+C3 k |
2 |
sh k 0+C4 k |
2 |
ch k 0= |
|
||||||||
dx2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
=−C 2+C4 =0; |
|
|
|
|
|
|
(3.62) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
d 2 V (l) |
=−C1 k |
2 |
sin kl−C2 k |
2 |
cos kl +C3 k |
2 |
sh kl +C4 k |
2 |
ch kl= |
|
|||||||
|
dx2 |
|
|
|
|
|
|
|||||||||||
|
|
=−C1 sin kl−C 2 coskl +C3 sh kl+C 4 ch kl=0. |
|
|
|
|
(3.63) |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
Из (3.60) и (3.62) вытекает, что C2=C4=0. Поэтому в системе остается |
||||||||||||||||||
два уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 sin kl +C3 sh kl=0; |
|
|
|
|
|
|
(3.64а) |
|||
|
|
|
|
|
|
|
|
−C1 sin kl +C3 sh kl=0. |
|
|
|
|
|
(3.64б) |
||||
Приравняем нулю определитель этой системы |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
−sinsinklkl shsh klkl =2sin kl sh kl =0. |
|
|
|
|
(3.65) |
||||||||
Поскольку kl≠0, то sin kl=0. Это значит, что kl=n π (n=1,2,...). Откуда, учитывая выражение для k (3.58), получим бесконечную последовательность квадратов собственных частот
|
|
2 |
4 |
EI z |
|
|
|
|
|
ωn=(π n) |
|
. |
|
(3.66) |
|
|
|
mx l4 |
|
||||
При |
kl=n π из (3.64а) |
и (3.64б) |
следует, |
что произвольная |
константа |
||
C3=0, т.к. |
C1 sin n π=0, а |
sh n π≠0. |
Тогда из |
(3.59) с учетом |
того, что |
||
C2=C3=C4 =0, получим |
|
|
|
|
|
|
|
|
|
V (x)=C1 sin kx. |
|
(3.67) |
|||
Произвольная константа C1 осталась неопределенной. Однако форму колебаний можно определить, задавшись некоторым значением этой константы, которая, таким образом, задает масштаб отображения амплитуд колебаний.
Пусть C1=1. Тогда с учетом того, что k= nlπ, формы колебаний можно определить по формуле
V n (x)=sin |
n π x |
. |
(3.68) |
|
|||
|
l |
|
|
64
Практическое значение для оценки прочности авиационных конструкций имеют низшие тона собственных колебаний (обычно определяется не более 50 тонов). Как правило, первый тон дает основную долю нагружения конструкции, поэтому очень важно определить именно его.
Из формулы (3.68) вытекает, что минимальная собственная круговая ча-
стота колебаний ω1 реализуется при n=1. Соответствующая форма колебаний показана на рис. 3.4 штриховой линией.
Колебания пластин
В случае пластин точные решения задачи определения собственных частот и форм колебаний могут быть получены только в некоторых частных случаях, когда дифференциальные уравнения колебаний могут быть решены точно при точно удовлетворенных граничных условиях. Примером такого случая могут служить прямоугольные пластины.
Выше было получено дифференциальное уравнение поперечных колебаний прямоугольной пластины (3.33), которое перепишем в виде
D 2 2 w+mxy |
∂2 w |
=q( x , y ,t ). |
(3.69) |
|
∂t2 |
|
|
Решение уравнения (3.69) должно удовлетворять граничным и начальным условиям.
Рассмотрим свободные колебания пластины, т.е. при q( x , y , t)=0
D 2 2 w+mxy |
∂2 w |
=0. |
(3.70) |
|
∂t2 |
|
|
Для шарнирно опертой по контуру пластины прогиб может быть представлен в форме двойного тригонометрического ряда, аналогичного используемому при рассмотрении вопросов устойчивости пластин (2.52)
∞ ∞ |
|
n π y |
|
|
w( x , y ,t)=sin ωt ∑ ∑ Amn sin m π x sin |
, |
|||
b |
||||
m=1 n=1 |
a |
|
||
где ω – неизвестная круговая частота колебаний; Amn – неизвестные коэффициенты;
a и b – длины сторон пластины.
Подставив решение (3.71) в уравнение (3.70), получим
D(m2 π2 + n2 π2 )2−mxy ω2=0.
a2 b2
(3.71)
(3.72)
Отсюда получим бесконечное множество квадратов собственных частот