
отчёт 1
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Лабораторная работа №1
ИССЛЕДОВАНИЕ МЕТОДОВ РЕШЕНИЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Вариант №5
Студент: гр. УТ – 21 Петухов П.А.
Преподаватель: Чуркин В.В.
Киров
2013 год
1.Задание.
1. В
Mathcad’е
по
заданному варианту уравнения построить график
построить график в диапазоне значений аргумента
в диапазоне значений аргумента
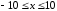 и найти значение корня
и найти значение корня
 (корней, если их несколько). Затем
построить график
(корней, если их несколько). Затем
построить график в диапазоне значений аргумента
в диапазоне значений аргумента
 и нанести на график линии сетки так,
чтобы одна из горизонтальных линий
проходила через нуль по оси ординат.
и нанести на график линии сетки так,
чтобы одна из горизонтальных линий
проходила через нуль по оси ординат.
2.
Составить алгоритм и написать код для
отделения корня (корней) уравнения в
диапазоне значений аргумента
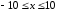 с шагом
с шагом

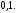
3.
Составить алгоритм и написать код для
уточнения значения корня (или одного
из корней, если их несколько) заданным
методом (методами). Получить таблицу и
графики зависимостей временных затрат
на уточнение корня от задаваемой
погрешности
(диапазон изменения
 ).
).
2.Графическая интерпретация
1) Отделение корней
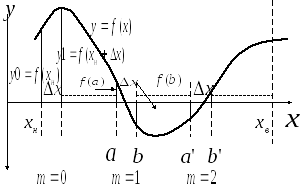
Для
отделения корней можно воспользоваться
методом линейного поиска, в котором
диапазон поиска
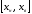 проходится с шагом
проходится с шагом
 при выполнении условия
при выполнении условия
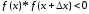 принимается решение о наличии корня в
промежутке
принимается решение о наличии корня в
промежутке
 .
В общем случае в диапазоне поиска может
оказаться несколько корней (
.
В общем случае в диапазоне поиска может
оказаться несколько корней ( ),
к каждому из которых следует применить
операцию уточнения.
),
к каждому из которых следует применить
операцию уточнения.
2)Уточнение корней методом деления пополам.


 -
функция действительной переменной x
и
известен интервал
-
функция действительной переменной x
и
известен интервал
 ,
на котором
,
на котором
 меняет знак. Следовательно, между
меняет знак. Следовательно, между
 и
и
 существует точка, в которой функция
обращается в нуль. Если разделить
интервал пополам и узнать, больше нуля
или меньше нуля функция в точке деления,
то можем указать подынтервал, в котором
функция меняет знак. Последующим делением
указываемых подынтервалов можно сколь
угодно близко подойти к корню: например,
за 10 шагов интервал с корнем будет
уменьшен в 1024 раза.
существует точка, в которой функция
обращается в нуль. Если разделить
интервал пополам и узнать, больше нуля
или меньше нуля функция в точке деления,
то можем указать подынтервал, в котором
функция меняет знак. Последующим делением
указываемых подынтервалов можно сколь
угодно близко подойти к корню: например,
за 10 шагов интервал с корнем будет
уменьшен в 1024 раза.
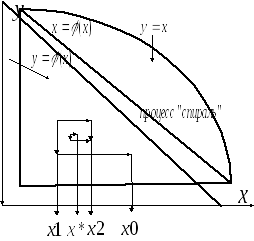
3)Уточнение корней методом итераций.
Уравнение
 заменяют
равносильным
заменяют
равносильным
 Выбирают
каким-либо способом приближенное
значение корня
Выбирают
каким-либо способом приближенное
значение корня
 и
по нему находят
и
по нему находят
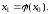 Повторяя процесс,
получают последовательность чисел:
Повторяя процесс,
получают последовательность чисел:


Если
эта последовательность - сходящаяся,
то предел
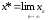 является
корнем равносильного уравнения и может
быть вычислен по итерационной формуле
является
корнем равносильного уравнения и может
быть вычислен по итерационной формуле

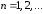 с
любой степенью точности.
с
любой степенью точности.
Процесс
итераций следует продолжать до тех пор,
пока для двух последовательных приближений
не будет выполнено неравенство
 где
где
 -
заданная абсолютная точность вычисления
корня и
-
заданная абсолютная точность вычисления
корня и
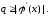
Поэтому
в методе итераций при переходе от
уравнения
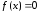 к уравнению
к уравнению
 следует
выбирать такое представление
следует
выбирать такое представление
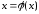 ,
при котором
,
при котором
 что
является условием сходимости метода
Чем меньше
что
является условием сходимости метода
Чем меньше

тем быстрее последовательные приближения
сходятся к корню
тем быстрее последовательные приближения
сходятся к корню


3.Алгоритмы
1)Отделение корней

2)Метод деления пополам

3)Метод
итераций
4)Комбинрованный метод

4. Таблица идентификаторов.
|
Имя переменной |
Тип переменной |
Диапазон |
Назначение |
|||||||
|
Алгоритм |
Программа |
|||||||||
|
xn |
xn |
double |
От ±5.0 × 10−324 до ±1.7 × 10308 |
Нижняя граница промежутка отделения корней |
||||||
|
xk |
xk |
double |
-----------//----------- |
Верхняя граница промежутка отделения корней |
||||||
|
dx |
dx |
double |
-----------//----------- |
Шаг |
||||||
|
a |
a |
double |
-----------//----------- |
Нижняя граница промежутка уточнения корней |
||||||
|
b |
b |
double |
-----------//----------- |
Верхняя граница промежутка уточнения корней |
||||||
|
c |
c |
double |
-----------//----------- |
Для сохранения значений границ |
||||||
|
d |
d |
double |
-----------//----------- |
Для сохранения значений границ |
||||||
|
eps |
eps |
double |
-----------//----------- |
Погрешность |
||||||
|
x |
x |
double |
-----------//----------- |
Рабочая переменная |
||||||
|
y |
y |
double |
-----------//----------- |
Рабочая переменная |
||||||
|
x1 |
x1 |
double |
-----------//----------- |
Рабочая переменная |
||||||
|
y1 |
y1 |
double |
-----------//----------- |
Рабочая переменная |
||||||
|
i |
i |
int |
От -2 147 483 648 до 2 147 483 647 |
Переменная цикла |
||||||
|
n |
n |
int |
-----------//----------- |
Счётчик числа корней |
||||||
|
m |
m |
int |
-----------//----------- |
Счётчик числа присваиваний |
||||||
5. Результаты выполнения задания
1)в
MathCade
2) в Buildere

Вывод: Комбинация методов повысила эффективность уточнения корней в диапазоне ошибки от 0,001 до 0,00001.
6.Библиографический список
В.В.ЧУРКИН ЧИСЛЕННЫЕ МЕТОДЫ (с алгоритмами и программами в среде C++Builder) Учебно-методическое пособие. 2013.
