Нелинейные задачи оптимального управления

Под нелинейными задачами будем понимать такие, в которых уравнения связи объекта

нелинейны по переменным и, хотя в большинстве случае имеет место нелинейность по управлению. К нелинейным задачам относятся также задачи, в которых подынтегральная функцияв функционале

нелинейна по переменным и.

Уравнения движения объекта, нелинейного по координатам с одним линейным управлением можно записать в следующей векторно-матричной форме:

,

где – вектор состояний объекта,

–функциональная матрица-столбец с элементами ,

–функциональная матрица-столбец с элементами .

Например, если задана электрическая печь со схемой:

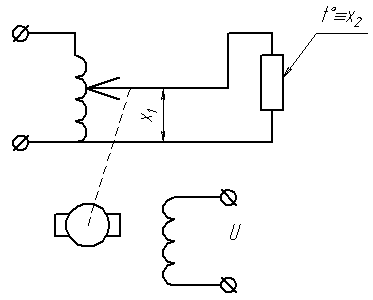
то из физических соображений можно записать систему нелинейных дифференциальных уравнений

,

что в матричной форме записи соответствует матрицам

, .

Системы с ограничениями ресурсов управления для нелинейных объектов.

Для объекта в форме

, (1)

требуется найти допустимое управление , доставляющее минимум интегральному функционалу

, (2)

характеризующему расход ресурсов управляемой системы или отклонения фазовых переменных системы. Поставленная задача называется задачей с ограничениями ресурсов.

Применим для решения задачи (1), (2) принцип максимума. Функция и вспомогательная система дляпривыглядит так:

Поскольку линейна по управлению,задано на замкнутом интервале, то, согласно теореме Вейерштрасса о максимуме линейной формы, максимумдостигается на границах ограничения по. Тогда оптимальное управление будет кусочно-непрерывным (что мы видели в задаче ТО) и определится выражением:

,

которое означает, что

.

Если на некотором интервале времени скалярное произведение и соответственно,, то принцип максимума позволяет однозначно определить оптимальное управление. Такая ситуация получила название вырожденной или особой и первая проблема, которая возникает при этом – проблема вычисления особого управления.

Кстати, возникновение особых режимов – признак сложности задачи, наиболее часто он встречается для NLO.

Для вычисления особого управления применяется несколько способов, которые можно разбить на две группы:

1. нахождение особого управления путем анализа вспомогательных переменных 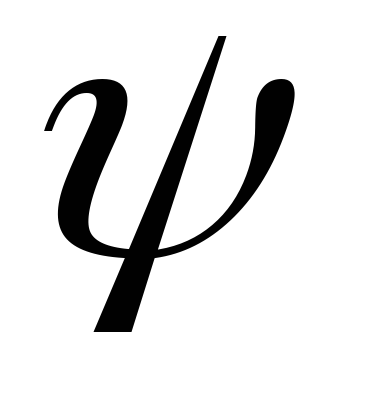(способ перебора управлений таких, чтобы).

2. определение особого управления в явном виде от переменных и параметров объекта (способ условий общности положения УОП).

Предпочтительнее, конечно, второй путь, т.к. исключение в сложных задачах практически не выполнимо.

Введем УОП для NLSв расширенном пространстве переменных размерностью (n+1). Определим дополнительную переменную, удовлетворяющую условию.

В пространстве получим расширенную систему (n+1) уравнений:

,

где ,,.

Пусть максимумдля расширенной системы достигается на грани или ребре многогранника ограничений по. Тогда на этом интервале временискалярное произведение

,

где – вектор, параллельный некоторой грани или ребру. На рисунке показана ситуация, когда неопределенной является величина управления.

Продифференцируем выражение nраз по времени, получим систему (n+1) уравнений:

, (3)

где векторы ,определяются из рекуррентного соотношения

, (4)

Далее определяем матрицу размера (n+1)x(n+1) как матрицу, столбцами которой являются векторы,.

.

Тогда система (3) преобразуется к виду:

,

которое всегда выполняется если матрица вырожденная или. Считается, что УОП выполняются, если. В противном случае из выражения дляможно выделить такие ситуации:

1. УОП не выполняется,

–

– имеется конечное число особых траекторий.

2. УОП не выполняется,

–

– определяем зависимости особого управления от переменных системы.

3. УОП не выполняется,

,

т.е. особая ситуация наблюдается при любых управлениях и оптимальное управление в задаче не единственное.

Рассмотрим пример.

Дан объект второго порядка

, ,

для которого требуется найти такое управление , которое доставляет минимум функционалу:

, – не задано.

В пространстве запишем

, .

По рекуррентному соотношению (4) вычисляем:

.

Составляем матрицу .

.

Определяем , откуда определяем особые управления.

Если провести численный анализ траекторий под действием управлений и, то оптимальными будут последовательности траекторий в зависимости от граничных условий:,,,,.