
- •Управление непрерывными динамическими тп Поиск экстремума функционалов
- •Свойства функций и функционалов
- •Классическое вариационное исчисление Метод Эйлера для определения экстремальных функций без ограничений
- •Решение вариационной задачи на безусловный экстремум при различных заданиях подынтегральной функции в функционале
- •Решение вариационных задач на условный экстремум (метод Эйлера-Лагранжа)
- •Решение задач акр с помощью кви
- •Решение задач акр с помощью метода Эйлера-Лагранжа
- •Решение неклассических задач вариационного исчисления
- •Принцип максимума
- •I. Решение задачи без ограничений на u.
- •II. Решение задачи с ограничениями.
- •Оптимальное по быстродействию управление линейными объектами
- •Теорема об nинтервалах
- •Нелинейные задачи оптимального управления
I. Решение задачи без ограничений на u.
![]()
![]()
Составляем функцию
Гамильтона
![]() :
:
![]() ,
,
т.к
![]() ,
то
,
то![]() .
.
Для оптимальности
управления требуется, чтобы
![]() доставляло максимум
доставляло максимум![]() .
Определяем экстремум
.
Определяем экстремум![]() по
по![]() :
:
![]()
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() доставляет максимум.
доставляет максимум.
Определим
вспомогательную переменную
![]() :
:
![]() .
.
Решая совместно уравнения связи и уравнение вспомогательной переменной

получаем
![]() ,
,![]() ,
,![]() .
.
II. Решение задачи с ограничениями.
Пусть сейчас на
![]() наложено ограничение
наложено ограничение![]() .
Сначала требуется решить задачу без
ограничений. Если ограничения существенны,
т.е. в задаче без ограничений получено
управление больше допустимого, то нужно
решать задачу с ограничениями. ПМ
позволяет решить вопрос о точке схода
с ограничения и управления после
ограничения.
.
Сначала требуется решить задачу без
ограничений. Если ограничения существенны,
т.е. в задаче без ограничений получено
управление больше допустимого, то нужно
решать задачу с ограничениями. ПМ
позволяет решить вопрос о точке схода
с ограничения и управления после
ограничения.
Доказывается, что в поставленной задаче (как и в любых других с квадратичным по управлению функционалом) управление выражается так:
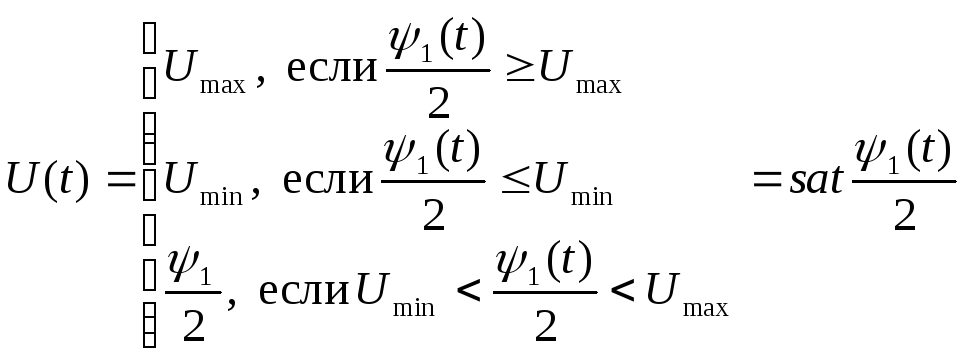 .
.
А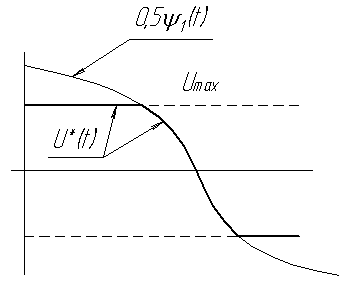 налитически
найти точку схода в общем случае
невозможно. Посмотрим как это можно
сделать численно из условия, что вдоль
оптимальной траектории
налитически
найти точку схода в общем случае
невозможно. Посмотрим как это можно
сделать численно из условия, что вдоль
оптимальной траектории![]() .
.
Пусть в момент времени

 ,
, .
.
![]()
![]() ,
т.е. в точке
,
т.е. в точке
![]() управление должно быть равно –0,3.
управление должно быть равно –0,3.
Возьмем интервал времени
 ,
, .
.
![]()
![]()
![]()
![]()
![]() ,
следовательно на интервале
,
следовательно на интервале
![]()
![]() .
.
Аналогично берем
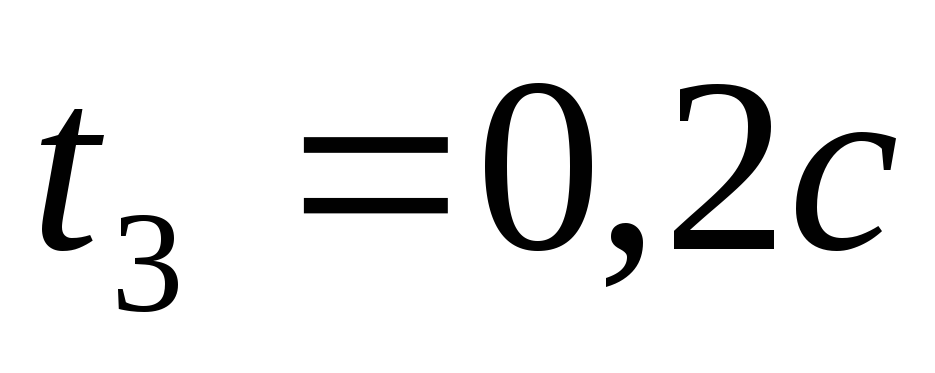
 .
.Далее
 ,
,
 ,
следовательно, здесь управление должно
лежать внутри ограничения. Искомая
точка схода будет зависеть от требуемой
точности решения, например, при точности
,
следовательно, здесь управление должно
лежать внутри ограничения. Искомая
точка схода будет зависеть от требуемой
точности решения, например, при точности
 время схода с ограничения
время схода с ограничения .
.
Итак, решение будет иметь следующий вид:
![]()

Оптимальное по быстродействию управление линейными объектами
Общая задача управления линейным стационарным объектом.Рассмотрим задачу определения оптимального в смысле быстродействия управления объектом, движения которого описывается системой обыкновенных дифференциальных уравнений с постоянными коэффициентами:
![]() ,
,
![]() .
.
Эту систему можно записать в векторной форме
![]() , (1)
, (1)
где ![]() –n-мерный вектор состояний
(координат);
–n-мерный вектор состояний
(координат);
![]() –r-мерный вектор управлений;
–r-мерный вектор управлений;
![]() – матрица размером
– матрица размером![]() ;
;
![]() – матрица размером
– матрица размером![]() .
.
Введем следующие
понятия. Систему (1) будем называть
полностью управляемой, если ее можно
перевести из любого заданного состояния
в любое желаемое за конечный промежуток
времени, выбирая надлежащим образом
закон изменения любой из компонент
![]() .
Это свойство называется свойством
управляемости.
.
Это свойство называется свойством
управляемости.
Управляемость
определяется строением матриц
![]() и
и![]() ,
т.е. физически структурой и типами
звеньев системы. Без доказательства
примем, что система (1) является полностью
управляемой если матрицаDвида:
,
т.е. физически структурой и типами
звеньев системы. Без доказательства
примем, что система (1) является полностью
управляемой если матрицаDвида:
![]()
размером
![]() имеет ранг
имеет ранг![]() .
.
Если система
управляема по каждой из компонент
вектора
![]() ,
то такая система называется нормальной.
Для того, чтобы линейная система с
постоянными коэффициентами вида (1) была
нормальной, необходимо и достаточно,
чтобы все матрицы
,
то такая система называется нормальной.
Для того, чтобы линейная система с
постоянными коэффициентами вида (1) была
нормальной, необходимо и достаточно,
чтобы все матрицы
![]() ,
,
![]()
были невырожденными,
т.е. имели ранг
![]() или определитель этих матриц не был
равен 0. Здесь
или определитель этих матриц не был
равен 0. Здесь![]() –k-тый столбец матрицы
–k-тый столбец матрицы![]() ,
который характеризует воздействиеk-той компоненты вектора
,
который характеризует воздействиеk-той компоненты вектора![]() .
Отметим, что каждая нормальная система
является полностью управляемой, тогда
как не всякая полностью управляемая
система является нормальной.
.
Отметим, что каждая нормальная система
является полностью управляемой, тогда
как не всякая полностью управляемая
система является нормальной.
Покажем это на примере.
Дана система с двумя входами и двумя выходами.
![]()
Матрицы
![]() и
и![]() имеют вид:
имеют вид:
![]() ,
,
![]()
Составим матрицу
![]() :
:
![]() ,
,
которая имеет
ранг, равный 2, при любых значениях
![]() ,
следовательно, система полностью
управляема.
,
следовательно, система полностью
управляема.
Для оценки
нормальности системы запишем матрицы
![]() и
и![]() :
:
![]()
![]()
Нетрудно видеть,
что матрица
![]() – невырожденная, а матрица
– невырожденная, а матрица![]() невырожденная при
невырожденная при![]() .
Если
.
Если![]() ,
то получаем систему, которая не управляется
с помощью одного из управлений
,
то получаем систему, которая не управляется
с помощью одного из управлений![]() .
.
Постановка
задачи.Во многих задачах автоматического
управления в качестве критерия
оптимальности выбирается быстродействие,
т.е. время перевода системы из положения![]() в положение
в положение![]() .
В этом случае минимизируемый функционал
имеет вид:
.
В этом случае минимизируемый функционал
имеет вид:

Пусть требуется решить линейную задачу быстродействия для объекта (1):
![]() ,
,
для которого заданы
начальное
![]() и конечное
и конечное![]() состояния. Область управления представляет
собой многогранник
состояния. Область управления представляет
собой многогранник
![]() ,
,
![]()
Функция Гамильтона для рассматриваемой задачи
![]() .
.
При
![]() и
и![]() получим:
получим:
![]() ,
,
что является довольно жестким ограничением. Более приемлемо ограничение
![]() .
.
Сопряженная система
уравнений для вспомогательных переменных
![]() :
:
![]() .
.
Согласно второму
условию принципа максимума, оптимальное
управление должно доставлять максимум
функции
![]() .
Максимум
.
Максимум![]() по
по![]() определяется только слагаемым
определяется только слагаемым![]() ,
следовательно, оптимальное управление
должно доставлять максимум этому
слагаемому. Можно показать, как в линейном
программировании, что оптимальным будет
управление, принадлежащее вершинам
многогранника
,
следовательно, оптимальное управление
должно доставлять максимум этому
слагаемому. Можно показать, как в линейном
программировании, что оптимальным будет
управление, принадлежащее вершинам
многогранника![]() .
Выражение
.
Выражение![]() достигает максимума если
достигает максимума если![]() принимает значения из кусочно-постоянной
функции
принимает значения из кусочно-постоянной
функции
![]() ,
,
![]()
или в общем виде
![]() .
.
Например, в системе
![]() ,
,
![]() ,
,![]()
![]()

Максимум
![]() по
по![]() определится максимумом
определится максимумом![]() .
.
![]()
Переменная
![]() зависит от времени, но максимум
зависит от времени, но максимум![]() лежит на границе
лежит на границе![]() .
Найдем
.
Найдем![]() :
:
![]()
![]() ,
,
![]()
![]()
![]()


Здесь не выяснен
вопрос, когда же значение переменной
сменится с
![]() на
на![]() (момент
(момент![]() )
и когда с
)
и когда с![]() переходить на
переходить на![]() .
Ответ на этот вопрос зависит от граничных
условий.
.
Ответ на этот вопрос зависит от граничных
условий.
