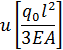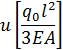матмод Желонкин
.doc
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
Вятский Государственный Университет
Инженерно-строительный факультет
Кафедра строительных конструкций
ЗАЧЕТНАЯ РАБОТА
По курсу «Математическое моделирование в строительстве»
Выполнил ст-т гр. СТ-22
___________________ Желонкин А.Ю.
Принял преподаватель
___________________ Буравлев В.Ф.
Киров 2014
Вариант 7-А
![]()
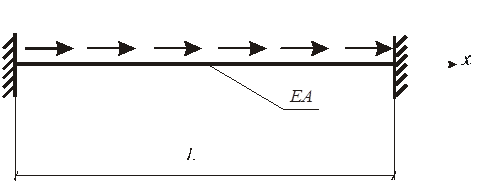
Рис. 1. Расчетная схема стержня
-
Точное решение
Дифференциальное уравнение равновесия имеет вид:
![]() (1.1)
(1.1)
Дважды интегрируем:
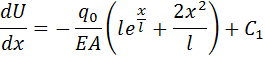
(1.2)
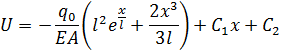
Удовлетворяем геометрическое граничное условие на левом торце:
![]()
откуда:
![]() (1.3)
(1.3)
Удовлетворяем геометрическое граничное условие на правом торце:

откуда:
![]() (1.4)
(1.4)
Внося полученные константы интегрирования (1.3) и (1.4) во второе соотношение (1.2), приходим к выражению для продольного перемещения:

(1.5)
Умножая на EА и беря производную по x, получим выражение для нормального усилия:
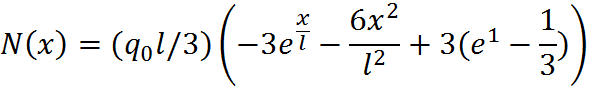
(1.6)
Произведем расчет перемещений и усилий по формулам (1.5) и (1.6) cпомощью программы на языке программирования «Pascal»в пяти равноотстоящих точках и сведем результаты расчета в таблицу 1.
PROGRAM STTR;
uses crt;
const
q=1.0;EA=1.0;l=1;m=4;
var i:integer;
uu,nn,dx,x,x2:real;
u,N: array[1..m+1] of real;
BEGIN
clrscr;
writeln;
writeln('Результат решения');
writeln;
writeln('Координата Перемещение Усилие');
dx:=1/m;
nn:=(q*l)/3;
uu:=nn*q*l*l/(EA*3);
for i:=1 to m+1 do begin
x:=dx*(i-1)/1;
X2:=sqr(x);
u[i]:={uu*}(-3*exp(x)-2*x*x*x+3*x*(exp(1)-1/3)+3);
N[i]:={nn*}(-3*exp(x)-6*x*x+3*(exp(1)-1/3));
writeln;
writeln ('x=', x:3, ' u=', u[i]:6:3, ' n=', n[i]:6:3);
end;
readln;
END. Таблица 1
|
|
0 |
0,25 |
0,5 |
0,75 |
1,0 |
|
|
0 |
0,905 |
1,381 |
1,169 |
0 |
|
|
4,155 |
2,928 |
0,709 |
-2,571 |
-7,000 |
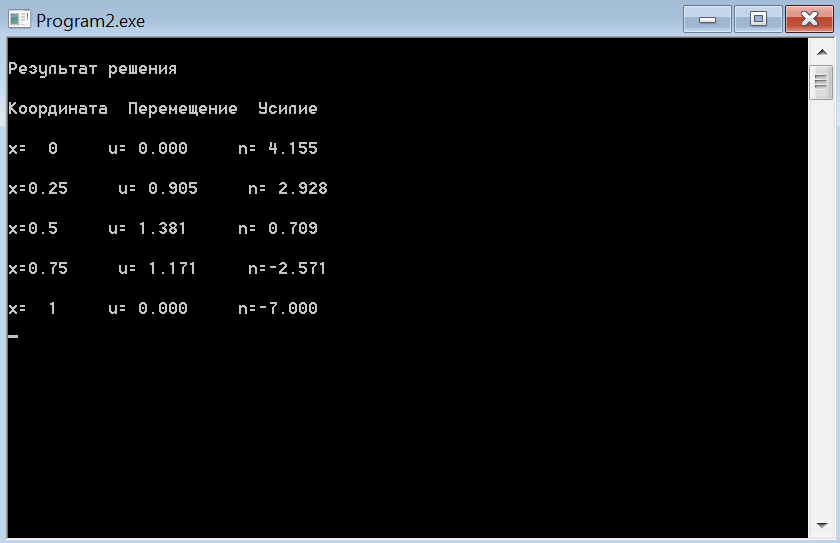
Представим результаты расчета в виде таблицы 1 и графиков (рис. 2, 3).
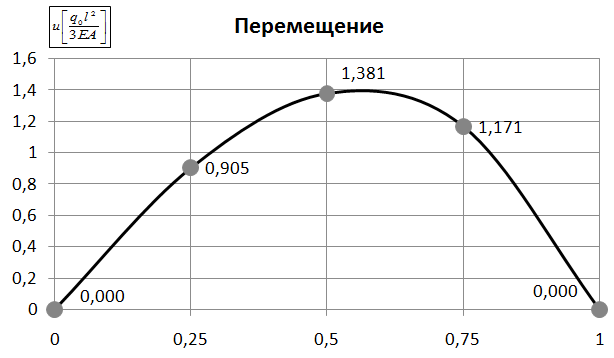
Рис. 2. Изменение перемещения по длине стержня (точное решение)
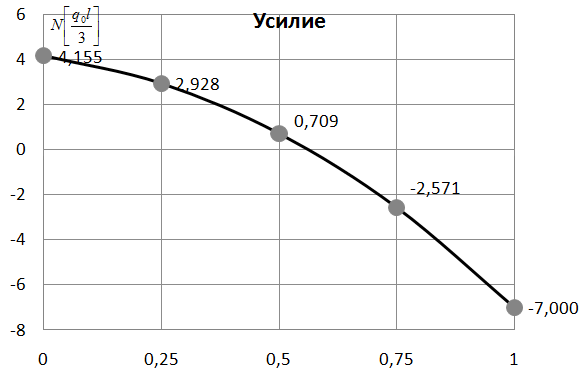
Рис. 3. Изменение продольного усилия по длине стержня (точное решение)
-
Приближенные решения
2.1 Метод конечных разностей
Обозначим узловые точки (1-5) в местах разбиения стержня на четыре участка (рис. 4).
![]()
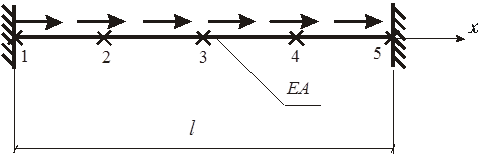
Рис. 4. Разбиение стержня на элементы
Запишем дифференциальное уравнение в конечно-разностной форме:
![]() (2.1.1)
(2.1.1)
Здесь введено обозначение
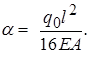 (2.1.2)
(2.1.2)
Запишем уравнение для всех внутренних точек:
![]()
![]() (2.1.3)
(2.1.3)
![]()
Преобразуем данные выражения и найдем u:
По условию: U1=0;U5=0
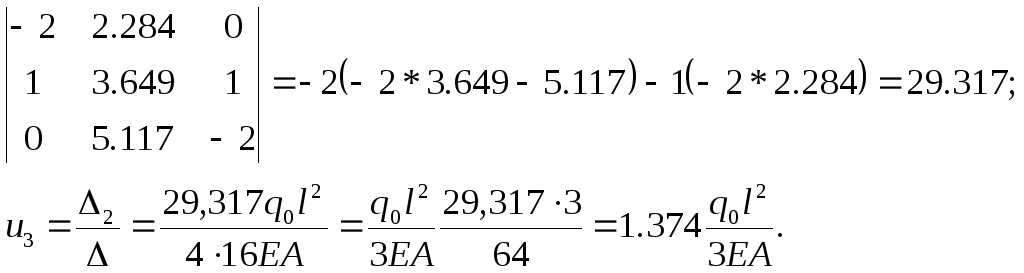
U2=-4,817α=![]()
U3=2(-4,817)+2,284α;
U3=-7,35α=![]()
U4=3(-4,817)+8,217α;
U4=-6,234α=![]()
Найдем перемещения, внося α и приводя результат к размерности точного решения.
![]() 4=-4,817α=
4=-4,817α=![]() =1,169
=1,169![]() ;
;
U3=-7,35α=![]() =1,379
=1,379![]() ;
;
U2=-4,817α=![]()
(2.1.6)
Осуществим переход к нормальным усилиям с учетом размерностей для перемещений и усилий в точном решении при помощи соотношения
Ni
= EA![]() =
=![]() (ui+1-ui)=
(ui+1-ui)=![]() q0l(ui+1-ui)=
q0l(ui+1-ui)=![]() q0l*2(ui+1-ui)
q0l*2(ui+1-ui)
(2.1.7)
где черта над u обозначает, что берутся только ее численные значения.
![]()
![]()
(2.1.8)
![]()
![]()
Воспользуемся соотношением, осуществляющим переход к усилиям с помощью дифференцирующей матрицы
![]() ,
(2.1.10)
,
(2.1.10)
которое в раскрытом виде с учетом числа элементов (h=l/4) и размерностей, использованных для перемещений и усилий в точном решении, запишется так:
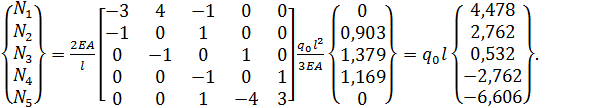 (2.1.11)
(2.1.11)
Результаты представлены в таблице 2 и на рисунке 3.
Таблица 2
|
|
0 |
0,25 |
0,5 |
0,75 |
1,0 |
|
|
0 (0) |
0,903 (0,905) |
1,379 (1,381) |
1,169 (1,171) |
0 (0) |
|
|
3,612* 4,478** (4,155) |
1,904* 2,762** (2,928) |
-0,28* 0,532** (0,709) |
-4,676* -2,762** (-2,571) |
-* -6,606** (-7,000) |
(…) – точное решение; * - решение в рамках МКР; ** - решение с помощью дифференцирующей матрицы.
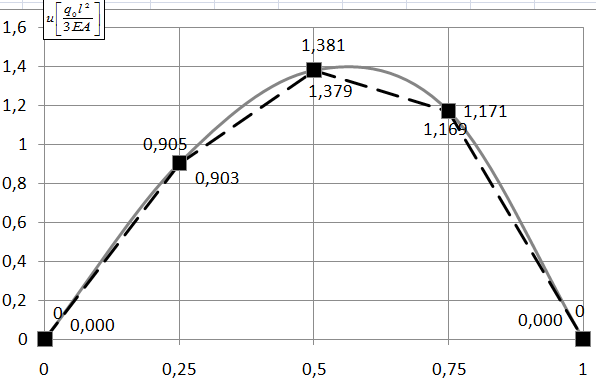
Рис. 5. Изменение перемещения по длине стержня (метод конечных разностей)

Рис. 6. Изменение продольного усилия по длине стержня (метод конечных разностей)
2.2 Метод Бубнова-Галеркина

Дифференциальное уравнение упругого равновесия растяжения – сжатия стержня имеет вид:
![]()
Запишем аппроксимирующую функцию:
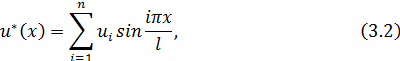
где
![]() - неизвестные параметры, подлежащие
определению;
- неизвестные параметры, подлежащие
определению;
![]() координатные
функции, удовлетворяющие граничным
условиям.
координатные
функции, удовлетворяющие граничным
условиям.
Внесем аппроксимирующую функцию в дифференциальное уравнение:
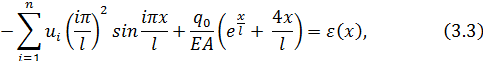
при
этом в правой части появляется функция
невязки ![]() ,
представляющая по физическому смыслу
неуравновешенную нагрузку.
,
представляющая по физическому смыслу
неуравновешенную нагрузку.
Неизвестные
параметры будем определять из условия
равенства нулю работы невязки на
возможных перемещениях, для чего умножим
уравнение почленно на возможное
перемещение![]() и
проинтегрируем по длине стержня.
и
проинтегрируем по длине стержня.
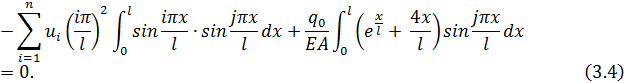
В силу ограниченности тригонометрических функций
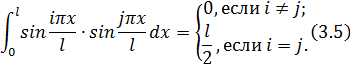
Остальные интегралы берутся по частям:
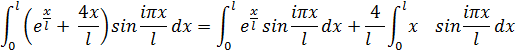
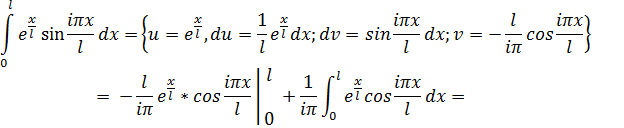
![]() =
=
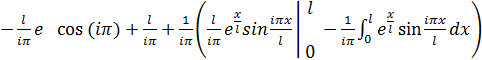
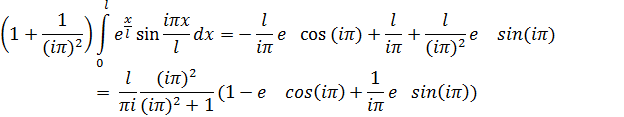
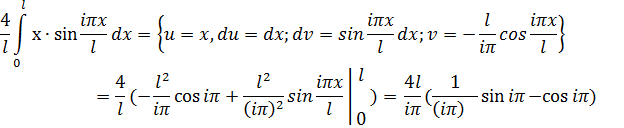
Внося значение интегралов в выражение для работы невязки навозможных перемещениях, приходим к равенству:
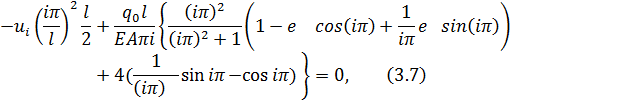
откуда
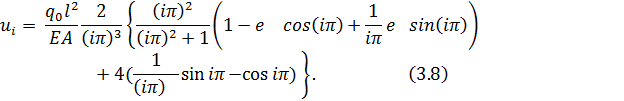
Выражение для перемещения с учетом размерности в точном решении принимает вид:

Дифференцируя по xи умножая на жесткость растяжения-сжатия ЕА, приходим к выражению для продольного усилия:
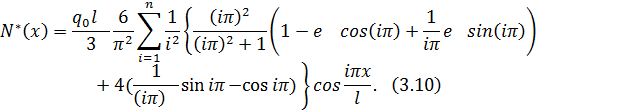
Program BH;
usescrt;
const
q=1.0;l=1.0;EA=1.0;m=4;mn=100;
var
i,j,k: integer;
dx,x,nn,uu,un,px,p,p1:real;
u,N:array[1..m+1] of real;
BEGIN
clrscr;
dx:=l/m;
nn:=6*l*q/sqr(pi);
uu:=nn*l/(EA*pi);
Writeln;
Writeln(' RezultatyraschetametodomBubnova-Galerkina ');
Writeln;
Writeln('KoordinataPeremeshenieUsilie ');
fork:=1 to m+1 do begin
x:=dx*(k-1)/l;
u[k]:=0;
N[k]:=0;
forj:=1 to mndo begin
i:=j;
p:=i*pi;
px:=p*x;
p1:=sqr(p)/(sqr(p)+1);
un:=(p1*(1-exp(1)*cos(p)+1/p*exp(1)*sin(p))+4*(1/p*sin(p)-cos(p)))/sqr(i);
N[k]:=N[k]+un*cos(px);
u[k]:=u[k]+un*sin(px)/i;
end;
Writeln;
Writeln (' x=',x:5:2,' u=',u[k]*uu:6:3,
' N=',N[k]*nn:6:3);
end;
readln;
END.
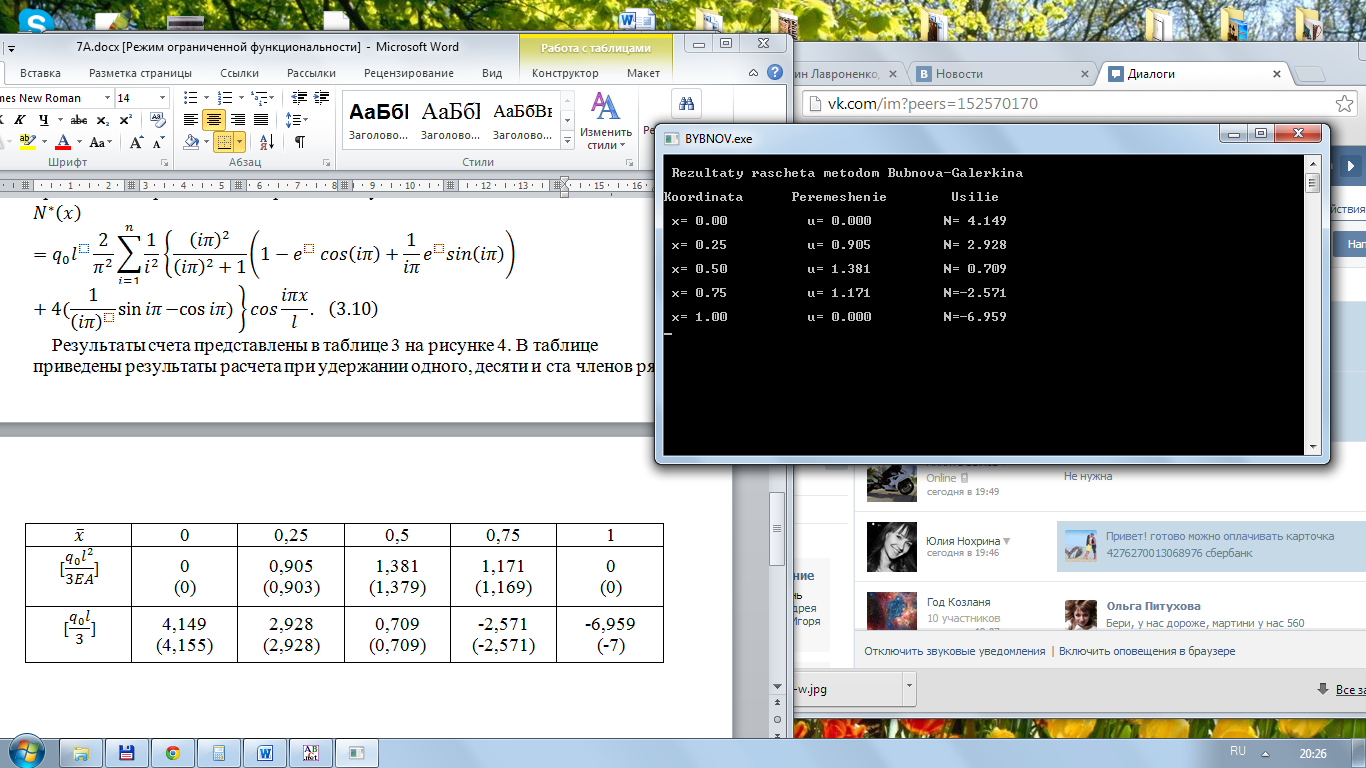
Результаты счета представлены в таблице 3 на рисунке 4. В таблице приведены результаты расчета при удержании одного, десяти и ста членов рядов (3.9) и (3.10), которые сходятся относительно быстро.
Таблица 3
|
|
0 |
0,25 |
0,5 |
0,75 |
1 |
|
|
0 (0) |
0,905 (0,903) |
1,381 (1,379) |
1,171 (1,169) |
0 (0) |
|
|
4,149 (4,155) |
2,928 (2,928) |
0,709 (0,709) |
-2,571 (-2,571) |
-6,959 (-7) |
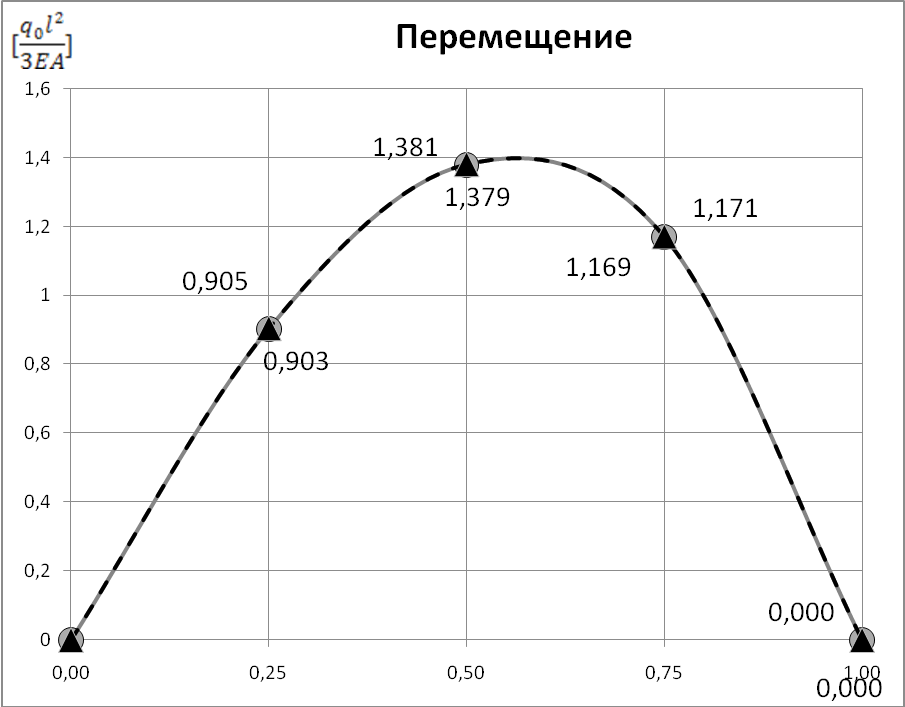
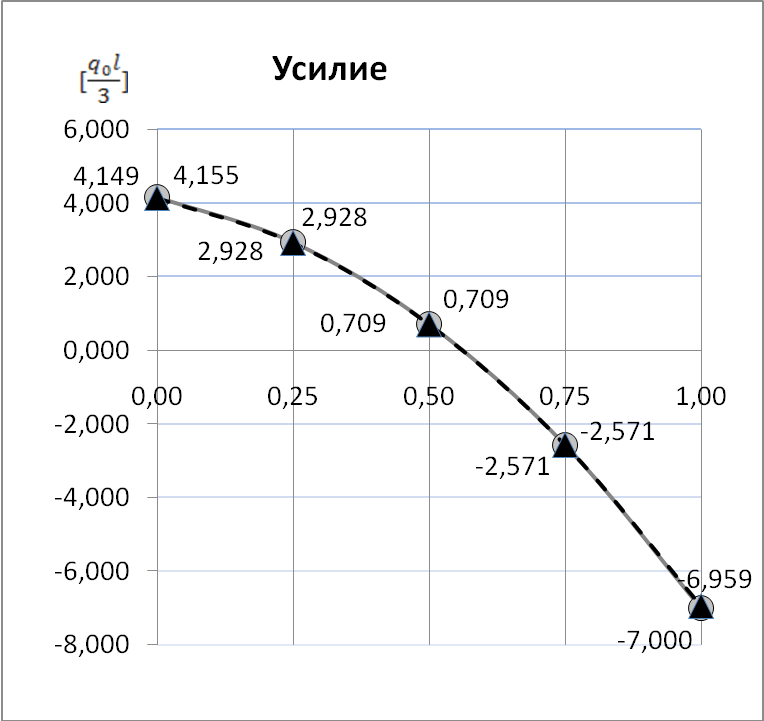
Рис.4. Изменение продольного перемещения и нормального усилия по длине стержня (метод Бубнова-Галеркина).
-
Метод конечных элементов
![]()
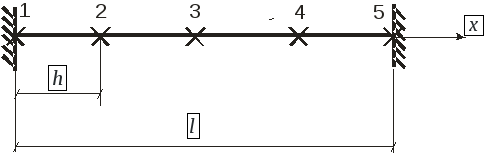
Для отдельного конечного элемента матрица жесткости имеет вид:
![]()
матрица преобразования нагрузки (грузовая матрица) –
![]()
вектор внешних нагрузок:
![]()
Матричное уравнение метода перемещений в конечноэлементной форме:
![]()
Здесь:
матрица жесткости всей системы - ![]() ,
формирующаяся в соответствии с топологией
системы; вектор неизвестных узловых
перемещений -
,
формирующаяся в соответствии с топологией
системы; вектор неизвестных узловых
перемещений - ![]() ;
грузовой вектор системы –
;
грузовой вектор системы –
![]()
содержащий
грузовую матрицу системы - ![]() и вектор внешних нагрузок системы -
и вектор внешних нагрузок системы - ![]() .
.
Учитывая число участков (конечных элементов), запишем (7.4) для нашего примера в раскрытом виде:
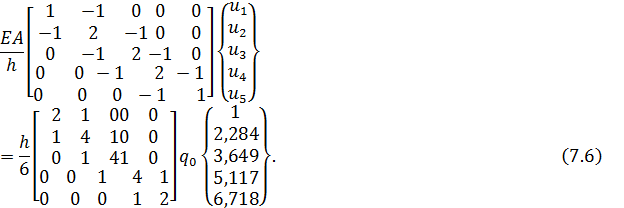
Умножая матрицу преобразования на вектор узловых значений нагрузки, перепишем (7.6) в виде:
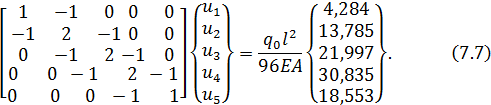
Геометрические
граничные условия (![]() и
и ![]() )
учтем, обнуляя строки и столбцы с общими
диагональными элементами – множителями
при
)
учтем, обнуляя строки и столбцы с общими
диагональными элементами – множителями
при ![]() и
и ![]() и соответствующие элементы грузового
вектора и заменяя
и соответствующие элементы грузового
вектора и заменяя ![]() ,
система (7.7) приобретает окончательный
вид:
,
система (7.7) приобретает окончательный
вид:
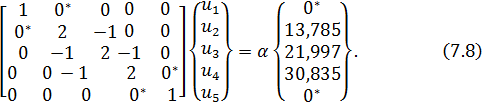
Данную систему трех уравнений удобно решать способом Краммера:
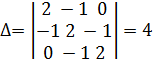 ;
;
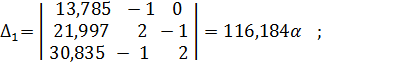

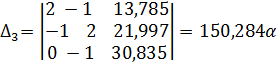
![]()
![]()
![]()
Осуществим переход к нормальным усилиям с помощью соотношения:
![]()
Первый элемент:
![]()
Второй элемент:
![]()
Третий элемент:
![]()
Четвертый элемент:
![]()
Воспользуемся дифференцирующей матрицей:
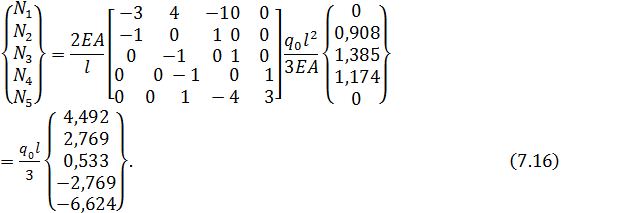
Результаты счета представлены в таблице 5 и рисунке 6.
Таблица 5
|
|
0 |
0,25 |
0,5 |
0,75 |
1 |
|
|
0 (0) |
0,908 (0,903) |
1,385 (1,379) |
1,174 (1,169) |
0 (0) |
|
|
3,631* 4,492** (4,155) |
1,908* 2,769** (2,928) |
-0,842* 0,533** (0,709) |
-4,696* -2,769** (-2,571) |
-* -6,624** (-7) |
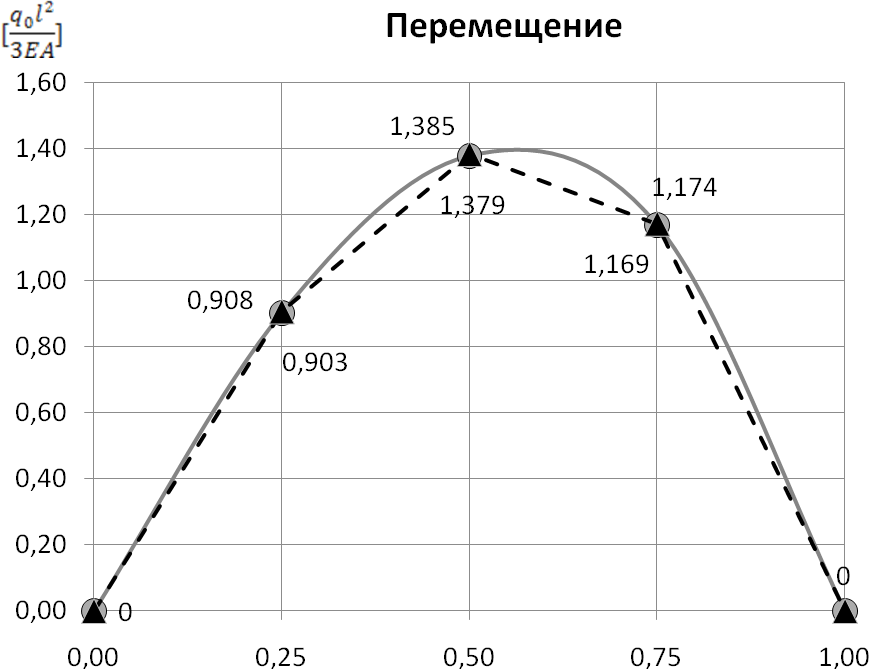
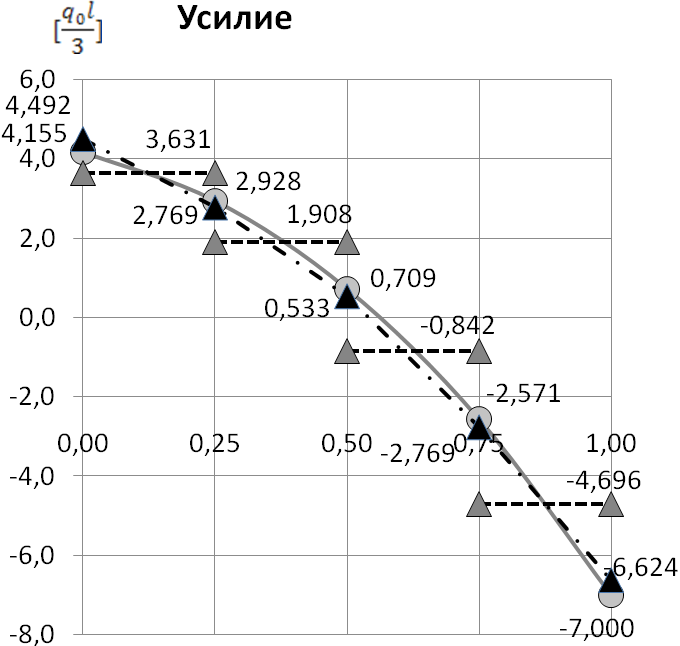
 -
точное решение;
-
точное решение;
 -
метод конечных элементов;
-
метод конечных элементов;
 -
с использованием дифференцирующей
матрицы.
-
с использованием дифференцирующей
матрицы.
Рис.6. Изменение продольного перемещения и нормального усилия по длине стержня (метод конечных элементов).