Взаимосвязь показателей эффективности.

Зависимость показателей эффективности от IRR проекта установим при заданных R, n, i.

1) Установим зависимость показателя NPV(i) от IRR. Изменяя инвестиции в проект I, тем самым изменяем показатель IRR проекта (см. зависимость IRR от I).

Имеем: NPV(i) = Ra_n,i – I, NPV(r) = Ra_n,r – I = 0. Тогда NPV(i) = Ra_n,i – Ra_n,r, где коэффициент дисконтирования ренты . Тогда,. Значит,NPV(i) – возрастающая вогнутая функция r на множестве , причем;;. График зависимостиNPV(i) от r показан на рисунке:

Рис. 1.7.11

Чем больше внутренняя норма доходности проекта r, тем больше его NPV(i). Отрицательные значения r соответствуют тому, что условие I < nR не выполняется, т.е. проект заведомо убыточен. NPV(i) < 0 если r < i и NPV(i) > 0 при r > i, что соответствует свойству 3 показателя IRR, параграф 1.6. Когда r принимает значение ставки дисконтирования i, тогда NPV(r = i) = = 0. Таким образом, чем больше IRR, тем более прибыльным является проект.

Замечание. Уточнить самостоятельно анализ зависимости NPV(i) от r и рисунок, если предположить, что .

2) Рассмотрим зависимость срока окупаемости n^* проекта (7.1) от его внутренней нормы доходности r при заданных R, n, i. Изменяя инвестиции I в проект, тем самым изменяем показатель IRR проекта.

Для существования срока окупаемости проекта (7.1) необходимо (но недостаточно), чтобы выполнялось условие (7.6). Следовательно, инвестиции I в проект таковы, что . Отсюда, так какI = Ra_n,r, то 1 - ia_n,r > 0. Это неравенство справедливо для значений r таких, что a_n,r < . Это значит, что, гдеr₀ - решение уравнения . Можно показать, что еслиin < 1, то r₀ < 0, а если in > 1, то r₀ > 0, причем r₀ < i. Найдем все решения уравнения (7.4) для . Те из них, которые удовлетворяют условиюn^*n, являются сроком окупаемости проекта.

Согласно определению срока окупаемости проекта и внутренней нормы доходности, Ra_n*,i = I = Ra_n,r. Отсюда a_n,r = a_n*,i, где . Тогда

.

Дифференцируем это выражение по r. Так как , то (a_n,r)^/_r < 0, (a_n,r)^//_rr > 0. Тогда (n^*)^/_r < 0, (n^*)^//_rr > 0. Значит, n^*(r) – убывающая выпуклая функция на множестве . Если, то. При этом,. Так как, то. В случае, когдаr₀ < 0, т.е. in < 1, можно найти значение n^* при r = 0. Действительно, так как , то.

График зависимости n^*(r) показан на рисунке, где использовано обозначение :

Рис. 1.7.12

Значения n^*n являются сроком окупаемости проекта. С увеличением внутренней нормы доходности r срок окупаемости проекта уменьшается. При r = i, где i – ставка дисконтирования проекта, срок окупаемости n^* = n , где n – срок проекта (см. свойство 2 срока окупаемости, параграф 1.6). При r < i проект не имеет срока окупаемости, так как этим значениям r соответствуют n^* > n. При r > i срок окупаемости n^* < n. Условие означает, что инвестиции в проект приближаются к значению стоимости вечной ренты, т.е.. Срок окупаемости такого проекта.

Пример 7.3. Расчет n^*(r), где r > r₀, приведен в таблицах для in < 1 и in > 1.

in < 1 (i = 5%, n = 3, r₀ = - 56,7%)

r	-50%	-30%	-10%	-0,1%	0,0%	5%	10%	50%
a n,r	14,00	6,385	3,717	3,006	3,331	2,723	2,487	1,407
n *	24,677	7,882	4,215	3,338	=3,734	n =3,000	2,721	1,496

in > 1 (i = 35 %, n = 3, r₀ = 2,47%)

r	2,48%	3%	10%	20%	35%	40%	50%
a n,r	2,86	2,829	2,487	2,106	1,696	1,589	1,4074074
n *	40,8458	15,350	6,809	4,454	n =3,000	2,706	2,2607

3) Рассмотрим зависимость индекса доходности d от внутренней нормы доходности r проекта при заданных R, n, i. Изменяя инвестиции в проект I, тем самым изменяем показатель IRR проекта.

Согласно определению индекса доходности и внутренней нормы доходности, имеем: ,I = Ra_n,r = . Так как, то, где. Кроме того, так как, то. Так как, то. Так какпри, то. Характер зависимостиd(r) показан на рисунке:

Рис. 1.7.13

Чем больше внутренняя норма доходности r проекта, тем больше его индекс доходности d, т.е. эффективность вложений. При r = i, где i – ставка дисконтирования проекта, d = 1. Если r < i, то d < 1 – проект не окупается. При r > i значения d > 1 – инвестиции эффективны.

Пример 7.4. Рассмотрим проекты

А( –90, 50, 50),

В( –100, 50, 50),

С( – 110, 50, 50).

Так как для проекта А выполняется условие I < nR (90<50 + 50), то внутренняя норма доходности этого проекта r^А > 0 и его индекс доходности d^А. Для проекта В имеемI = nR, что соответствует значениям r^В = 0 и d^В . Для проекта С выполняется условиеI > nR, что означает заведомую убыточность проекта, r^С < 0 и значение индекса доходности d^С < d^В < 1.

Замечание. Уточнить самостоятельно анализ зависимости d(r) и рисунок, если предположить, что .

Итак, зависимость показателей эффективности от внутренней нормы доходности IRR проекта можно охарактеризовать следующим образом: NPV(i), PI – возрастающие функции r, срок окупаемости DPP – убывающая функция r. Следовательно, при увеличении IRR проекта все показатели указывают на возрастание эффективности проекта, включая сам показатель IRR, что снова означает согласованность показателей в оценке проекта.

Зависимость показателей эффективности от NPV(i)  проекта установим при заданных R, n, i.

1) Рассмотрим зависимость срока окупаемости n^* проекта (7.1) от его NPV(i). Изменяя инвестиции I в проект, тем самым изменяем показатель NPV(i) проекта.

Для существования срока окупаемости проекта (7.1) необходимо (но недостаточно), чтобы выполнялось условие (7.6). Значит, инвестиции I в проект таковы, что . Следовательно, показательNPV(i) = Ra_n,i – I будем рассматривать для значений . ТогдаNPV(i) . Учитывая равенство (7.4), имеемNPV(i) = Ra_n,i – I = Ra_n,i - Ra_n*,i = Ra_n,i - R. Отсюда несложно установить, чтоn^*(NPV(i)) - убывающая выпуклая функция, характер зависимости которой имеет вид:

Рис. 1.7.14

Значения n^*n являются сроком окупаемости проекта. Заметим, что n^*n когда NPV(i) 0, что соответствует свойству 4 DPP. С увеличением NPV(i) срок окупаемости проекта уменьшается. На этом рисунке значению n^* = n, где n – срок проекта, соответствует NPV(i) = 0. Проекты с NPV(i) < 0 не имеют срока окупаемости, что подтверждает свойство 4 DPP, параграф 1.6.

2) Рассмотрим зависимость индекса доходности d проекта (7.1) от его NPV(i) при заданных R, n, i. Изменяя инвестиции I в проект, тем самым изменяем показатель NPV(i) проекта.

Имеем: =, где в общем случае NPV(i).

Х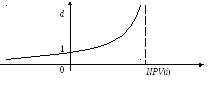арактер зависимостиd(NPV(i)) имеет вид:

Рис. 1.7.15

С увеличением показателя NPV(i) проекта его индекс доходности растет. Значения индекса доходности d > 1 имеют проекты с NPV(i) > 0, что подтверждает свойство 4 показателя PI, параграф 1.6.

Замечание. Уточнить самостоятельно анализ зависимости d(NPV(i)) и рисунок, если предположить, что .

Таким образом, срок окупаемости уменьшается, а индекс доходности увеличивается при увеличении NPV(i) проекта. С учетом ранее рассмотренной зависимости показателей NPV(i) и IRR, можно утверждать, что с увеличением NPV(i) все показатели, включая сам показатель NPV(i), указывают на возрастание эффективности проекта. 

Связь срока окупаемости n^* и индекса доходности d установим при заданных R, n, i. Изменяя инвестиции в проект I, тем самым изменяем его срок окупаемости n^* (см. зависимость DPP от I).

Согласно определению индекса доходности и срока окупаемости, имеем: ,Ra_n*,i = I. Тогда , где. Так как,, то,

. Следовательно, d(n^*) – убывающая выпуклая функция на множестве . Так как, то< 1. Так как, то. График зависимостиd(n^*) показан на рисунке:

Рис. 1.7.16

Значения n^*n являются сроком окупаемости проекта. С увеличением срока окупаемости проекта n^* его индекс доходности уменьшается, т.е. оба показателя указывают на снижение эффективности проекта (см. пример 7.1). При n^* = n, где n – срок проекта, d = 1 (свойство 3 показателя PI). Индекс доходности d > 1 тех проектов, которые имеют срок окупаемости n^*< n. И наоборот: проекты, не имеющие срока окупаемости (для этих проектов n^*> n), имеют d < 1. Таким образом, анализ зависимости d(n^*) приводит к ранее полученным выводам.

Рассмотренные в этом параграфе зависимости показателей эффективности от параметров проекта и связь показателей подтверждают согласованность показателей в оценке проекта, установленную в параграфе 1.6: если какой-либо из показателей изменяется и указывает, например, на повышение эффективности проекта по этому показателю, то и остальные показатели при этом изменяются так, что проект оценивается как более эффективный и по всем остальным показателям. И наоборот: снижение эффективности проекта по одному из показателей означает точно такой же вывод в отношении остальных показателей. Очевидно, что снижение эффективности по разным показателям происходит в разной мере. Окончательная оценка проекта – за лицом, принимающим решение о финансировании проекта.

Заметим, что здесь рассматривались лишь проекты с классической схемой инвестирования – сначала расходы, затем отдача. Проекты с неординарными денежными потоками и проблемы выбора проектов для реализации среди альтернативных рассмотрены в специальной литературе, например [5, 10].

119