1.7. Зависимость показателей эффективности от параметров инвестиционного проекта.

Параметры проекта – это величины членов денежного потока, их распределение во времени и процентная ставка дисконтирования. Зависимость показателей эффективности от параметров проекта классического характера рассмотрим для проекта, в котором инвестиции - разовые в момент t = 0 в размере I, поток доходов – постоянная годовая обычная (неотложенная) рента в течение n лет. Годовой доход R. Ставка дисконтирования проекта – годовая процентная ставка i. Проект описывается финансовым потоком вида

(-I, R,…, R). (7.1)

Показатели эффективности проекта (7.1) рассчитываются на основе современных стоимостей потока доходов Ra_n,i и инвестиций I.

Чистая современная стоимость проекта при процентной ставке i:

NPV(i) = Ra_n,i – I , (7.2)

Значение показателя IRR - решение уравнения доходности NPV(r) = 0, которое для проекта (7.1) имеет вид:

Ra_n,r – I = 0. (7.3)

Срок окупаемости n^* определяется из уравнения:

Ra_n*,i = I (7.4)

Индекс доходности проекта (7.1) равен:

. (7.5)

Зависимость показателей эффективности от срока проекта (периода отдачи) n рассмотрим, считая заданными размеры вложенных инвестиций I, поступающих платежей R и процентную ставку дисконтирования i. Срок проекта (7.1) совпадает с его периодом отдачи. Параметры I, R, i определяют окупаемость проекта. Действительно, при заданных I, R, i условие возврата инвестиции, или, что тоже самое, условие существования срока окупаемости проекта, - это условие разрешимости уравнения (7.4), т.е. задачи о сроке ренты (см. параграф 1.5). Условие существования срока окупаемости проекта запишем в виде:

(7.6)

1) Рассмотрим зависимость показателя NPV(i) от срока n проекта при заданных I, R, i. Чистая современная стоимость проекта (7.1) рассчитывается по формуле:

NPV(i) = Ra_n,i – I ,

коэффициент дисконтирования ренты , где(не только целое, см.Замечание в параграфе 1.5). Тогда ,. Следовательно,NPV(i) – возрастающая вогнутая функция n на множестве , причем,. Значение последнего предела – этоNPV(i) проекта, в котором поток доходов – вечная рента. Если считать, что параметры i, R, I проекта (7.1) таковы, что выполняется условие (7.6), то существует единственная точка n^* > 0 такая, что

= NPV_n*(i) = 0.

Согласно свойству 3 срока окупаемости (параграф 1.6), n^* - срок окупаемости (DPP) проекта (7.1). Таким образом, неравенство (7.6) является не только условием существования срока окупаемости проекта (7.1), но и условием существования проектов с NPV(i) 0.

График зависимости показателя NPV(i) от срока проекта n показан на рисунке 1.7.1:

Рис. 1.7.1

Чем больше срок проекта (7.1), тем больше его NPV(i). Найдем n^* из уравнения NPV_n*(i) = 0, что равносильно уравнению (7.4), при условии (7.6):

. (7.7)

Если n^*, определенное по (7.7), удовлетворяет условию n^* n, где n – срок проекта, то (7.7) - формула точного значения срока окупаемости проекта (7.1) (см. определение срока окупаемости, параграф 1.6). Если срок проекта n < n^*, то проект не имеет срока окупаемости. При этом его NPV(i) < 0. Чтобы проект окупался при данных ставке i, инвестициях I и доходах R необходимо, чтобы продолжительность проекта была не меньше n^*.

2) При заданных значениях I, R, i установим зависимость показателя IRR проекта (7.1) от его срока n. Из уравнения (7.3) имеем a_n,r = , где. Дифференцируем это выражение поn: . Отсюда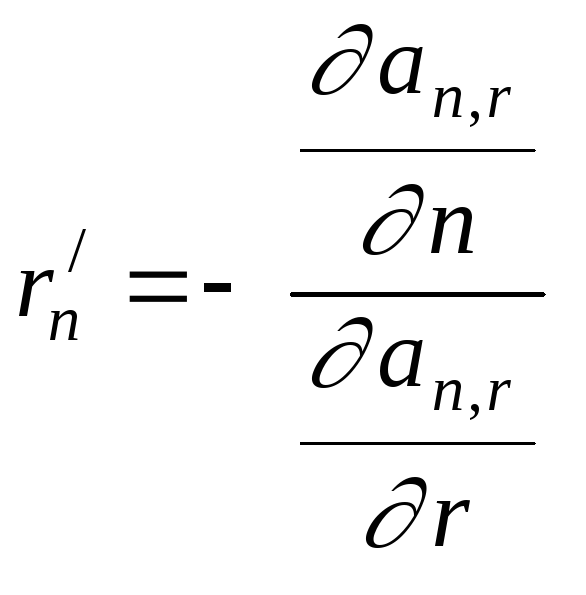. Так как, то. С другой стороны, так как, то. Следовательно,. Значит,r(n) - возрастающая функция на множестве . Так какдля каждого конечного n > 0, то . Отсюдаприипри. Кроме того, еслиr = 0, то . График зависимостиr(n) показан на рисунке 1.7.2:

Рис. 1.7.2

С увеличением срока проекта (7.1) его показатель IRR возрастает, приближаясь к значению IRR проекта, поток доходов которого – вечная рента. Заметим, что если срок проекта меньше, то доходность проекта отрицательна. И наоборот – значениямr > 0 соответствуют сроки проекта (см. условие разрешимости задачи о процентной ставке ренты, параграф 1.5). Приr = i срок проекта n совпадает с его сроком окупаемости n*, т.е. n = n* (свойство 2 срока окупаемости, параграф 1.6). Значениям r < i соответствует срок проекта n < n* - проект является убыточным (свойство 3 показателя IRR, параграф 1.6) и не имеет срока окупаемости (см. свойство 5 срока окупаемости, параграф 1.6). При r > i срок проекта n > n* - проект прибыльный и имеет срок окупаемости.

3) Рассмотрим зависимость индекса доходности d от срока n проекта (7.1) при заданных i, R, I. Будем считать, что параметры i, R, I проекта таковы, что выполняется условие (7.6): .

Согласно определению, индекс доходности проекта (7.1) рассчитывается по формуле (7.5). Тогда

= ,

где . Отсюда

.

Характер зависимости d(n) показан на рисунке:

Рис. 1.7.3

С увеличением срока проекта (7.1) его показатель PI возрастает, приближаясь к значению PI проекта, поток доходов которого – вечная рента. Значению d = 1 соответствует срок проекта n = n^*, где n^* - срок окупаемости проекта (свойство 3 PI, параграф 1.6). Если n > n^*, то проект имеет срок окупаемости, при этом d > 1. При n < n^* проект не имеет срока окупаемости, его индекс доходности d < 1.

Заметим, что условие (7.6) обеспечило существование проектов, индекс доходности которых d 1.

Итак, показатели NPV(i), IRR, PI возрастают при увеличении срока проекта (7.1). При этом срок окупаемости проекта существует, когда его NPV(i)0,PI 1, а следовательно,IRR i (см свойство 5 PI, параграф 1.6), т.е. когда все остальные показатели указывают на приемлемость проекта. Заметим, что неравенство (7.6) при условии, что срок проекта n n^*, обеспечивает приемлемость проекта по всем показателям, что также подчеркивает согласованность показателей в оценке проекта.

Замечание. Чем более протяжен во времени проект, тем более тщательная оценка требуется для членов денежного потока последних лет реализации проекта. Здесь инвестиционный проект рассматривается в условиях определенности, когда поступление платежей точно в срок и в полном объеме считается гарантированным.

Зависимость показателей эффективности от величины вложенных инвестиций I рассмотрим, считая заданными срок проекта n, размеры поступающих платежей R и ставку дисконтирования i.

1) Увеличение инвестиций в проект влечет уменьшение его IRR (формула 6.14). Рассмотрим подробнее зависимость показателя IRR проекта (7.1) от величины инвестиций I.

Уравнение NPV(r) = 0 для проекта (7.1) имеет вид: I = Ra_n,r, где . Так как,, то,. Значит,r(I) – убывающая выпуклая функция на множестве значений I. Если, то; еслиr = 0, то I = nR; если , то. График зависимостиr(I) показан на рисунке:

Рис. 1.7.4

С увеличением инвестиций I доходность проекта r уменьшается. При I > nR доходность отрицательна, r < 0, проект заведомо убыточен. На этом рисунке значению r = i, где i – ставка дисконтирования проекта, соответствует максимальный уровень затрат I_max, при котором проект не является убыточным. Действительно, NPV(r = i) = 0, откуда I_max = Ra_n,i. Если I > I_max , то r < i , что означает убыточность проекта (см. свойство 3 IRR, параграф 1.6). И наоборот, значениям I < I_max соответствуют r > i, при которых проект является прибыльным.

Замечание. Если исходить из того, что инвестиции в проект не могут превышать стоимости вечной ренты, т.е. выполняется условие (7.6): , тогда анализ функцииr(I) требует уточнения. Рекомендуется рассмотреть это самостоятельно.

2) Чистая современная стоимость проекта (7.1) рассчитывается по формуле:

NPV(i) = Ra_n,i – I .

Определим множество значений показателя. Если считать, что Iпри заданныхR, n, i, то NPV(i) . Если предполагается, что, тоNPV(i) , где< 0.