17

17.

Напряженность электрического поля.

Физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в данную точку поля: .

(единица 1 Н/Кл=1 В/м)

1 Н/Кл – напряженность такого поля, которое на точечный заряд 1 Кл действует силой 1 Н.

Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд (заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле)).

Напряженность поля точечного заряда в вакууме.

, где - радиус-вектор, соединяющий данную точку поля с зарядом Q, или в скалярной форме .

Направление вектора совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор направлен к заряду.

Линии напряженности (силовые линии).

Линии, касательные к которым в каждой точке совпадают с направление вектора .

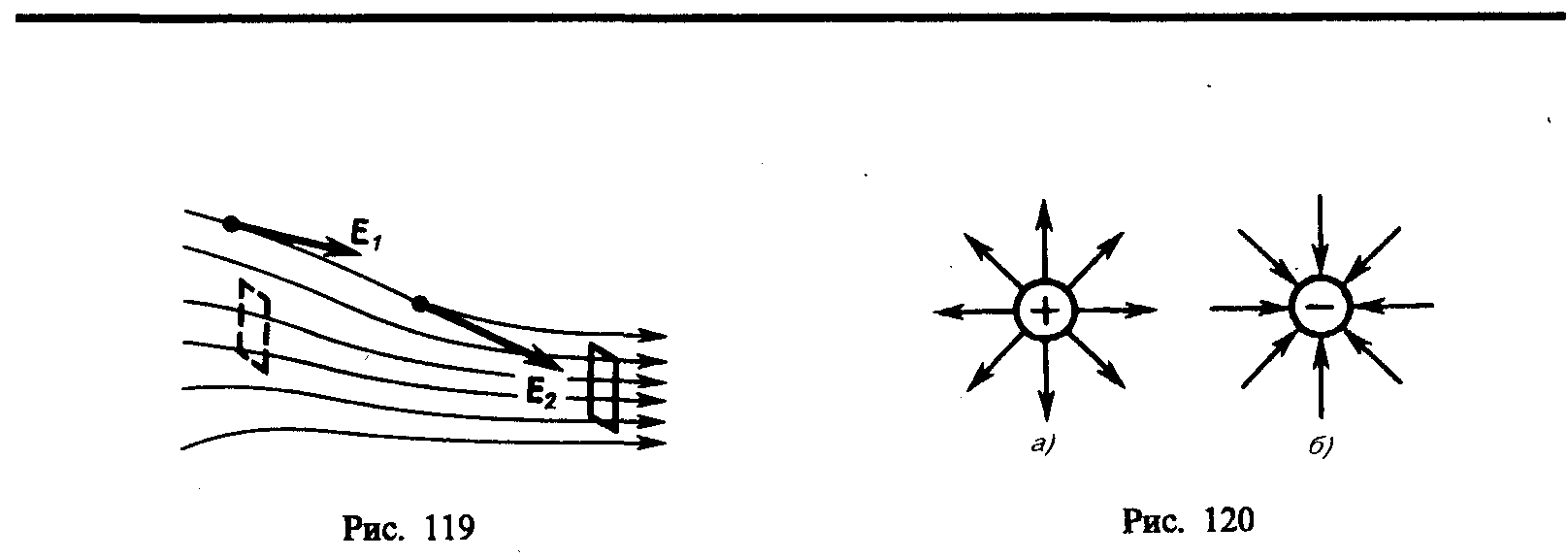
Для однородного поля (когда вектор напряженности в любой точке постоянен по модулю и направлению) линии напряженности параллельны вектору напряженности.

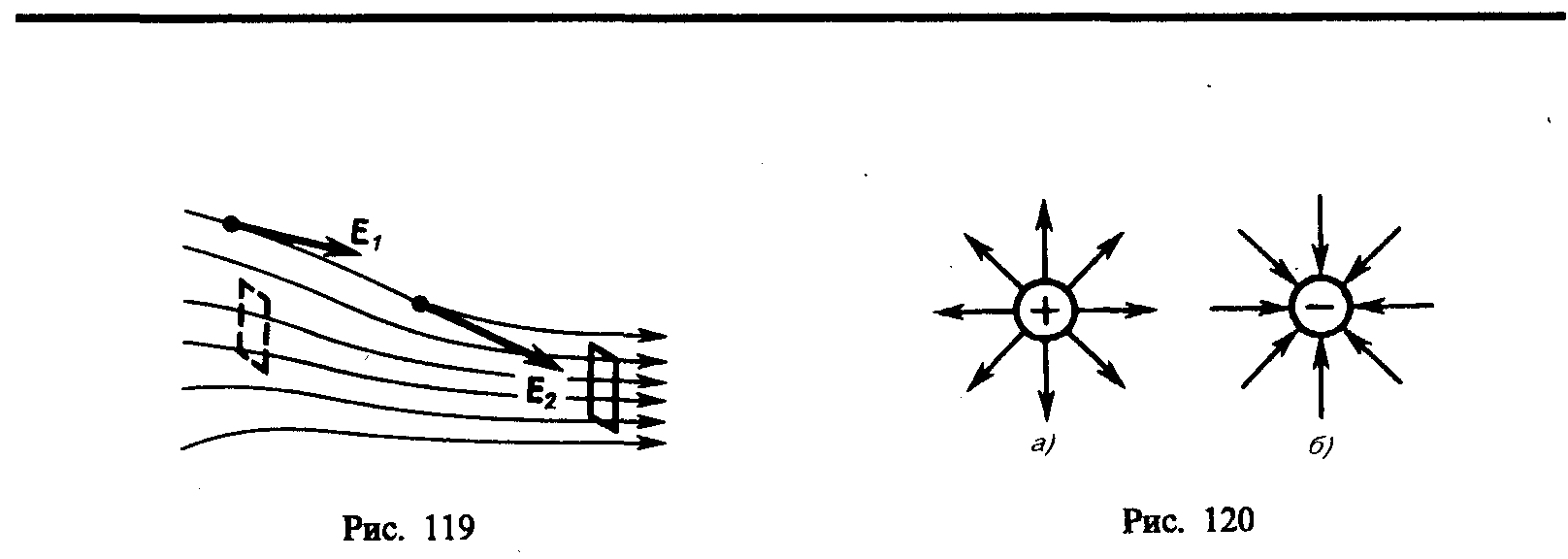
Если поле создается точечным зарядом, то линии напряженности – радиальные прямые, входящие из заряда, если он положителен (а), и входящие в него, если заряд отрицателен (б).

Поток вектора .

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, их проводят с определенной густотой: число линий

Т.Гаусса.

Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Рассмотрим общий случай произвольной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции напряженность Е поля, создаваемого всеми зарядами, равна сумме напряженностей E_i полей, создаваемых каждым зарядом в отдельности: Поэтому

Каждый из интегралов, стоящий под знаком суммы, равен Q_i /₀. Следовательно,

(81.2)

Формула (81.2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ₀.