Добавил:

plehanov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский экономический университет им. Г.В. Плеханова

Предмет:

Теория вероятностей и математическая статистика

Файл:

Теория вероятностей в примерах и задачах

.pdf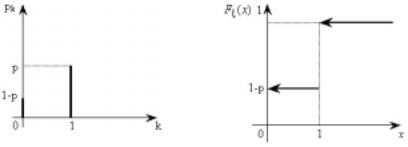

Скачиваний:

326

Добавлен:

03.10.2013

Размер:

850.21 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Рис. 6.1		Рис.6.2
2) СВ î(ù) имеет биномиальное распределение, если
		î(ù ) {0 ,1, 2 ,...,n} ,
pk = P{ù:î(ù) =	k} =	Cnk pk (1− p)n− k ,k = 0,1,2,...,n, 0 < p < 1,
		l
	∑	Cnk pk (1− p)n− k , l < x ≤ l + 1,
		= 0
	k	= 0
Fî(x) =
Fî(x) =	1, x > n,

0, x ≤ 0,

отметим, что, как следует из формулы Бернулли, число появлений события в n независимых испытаниях Бернулли имеет биномиальное распределение;

3)СВ î(ù) имеет геометрическое распределение, если

ξ(ω ) {0,1, 2, ...k, ...} ,

	pk = P{ù:î(ù)
		0, x ≤ 0
Fî	(x) =
Fî	(x) =	∑l	p(1−

		k =	0

= k} =

p(1

−

p)k ,k =

0,1, 2,...,0 <

p < 1,

0, x ≤

x ≤

l +

− (1

− p)l ,l

< x ≤ l + 1;

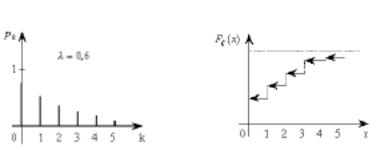
4)CB î(ù) имеет распределение Пуассона с параметром

ë> 0, если

{0,1, 2,...k,...} ,

pk = P{ù: î(ù) =		k} =			ëk	e− λ ,k =	0,1, 2, ..., рис. 6.3.,
pk = P{ù: î(ù) =		k} =			k!	e− λ ,k =	0,1, 2, ..., рис. 6.3.,
					k!
	0, x ≤		0,
Fξ (x) =							l + 1, рис. 6.4.;
Fξ (x) =	e− λ ∑l			λk		,l < x ≤	l + 1, рис. 6.4.;
		k =	0		k!

Рис. 6.3

Рис. 6.4

Дадим интерпретацию некоторых из этих СВ. Предположим, что студент идет сдавать зачет. На некоторые вопросы по сдаваемому предмету он знает ответы, а на остальные – нет. Поэтому событие, заключающееся в том, что он получит зачет, является случайным. Определим СВ следующим образом: если зачет сдан, то ξ = 1 , если нет, то ξ = 0 . Таким образом, определенная СВ является бернуллиевой, параметр p в том случае соответствует относительному числу вопросов, на которые студент знает ответ. Пусть студенту необходимо сдать n зачетов и он делает по одной попытке получить каждый из этих зачетов. Определим СВ ξ как число зачетов, которые получит студент. Такая СВ будет биномиальной. Число студентов, которых успел выслушать преподаватель на зачете за фиксированный интервал времени, а также число заданий, которые выполняет ЭВМ за фиксированный

промежуток времени, являются СВ, распределенными по закону Пуассона с соответственно определенными параметрами λ .

Пример 6.4. Производятся последовательные испытания трех приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Составить таблицу распределения и найти ф.р. случайного числа испытанных приборов, если вероятность надежности каждого

прибора равна q = 1− p =		0, 9 .
Решение. СВ ξ , описывающая число испытанных приборов,
имеет распределение вероятностей
							k − 1
	pk = P{ξ =	k}	p(1−			p)	k − 1	, k = 1, 2,
			p(1−			p)		, k = 1, 2,
			=	−	p)k − 1, k = 3,
			(1	−	p)k − 1, k = 3,

поэтому таблица распределения имеет вид

	k		1			2			3

	pk	0,1			0,9·0,1				0,92·0,1
			0, x ≤ 1,

	а ф.р. F (x) =		k		p , k < x ≤ k + 1,
	ξ		∑		i
	ξ				i
			i= 1
					3.
			1, x ≥		3.
II. Непрерывные СВ (СВ с абсолютно непрерывными
ф.р.). В этом случае Fξ (x) −			непрерывная функция и
	Fξ (x) = ∫x			pξ (t)dt.
			− ∞

Ясно, что

pξ (x) = dFξ (x) dx

в точках существования производной. Функция pξ (x) называется плотностью распределения вероятностей СВ ξ (ω ). Она обладает следующими свойствами:

1)	pξ (x) ≥	0 (как производная неубывающей функции);
	∞
2)	∫ pξ (x)dx = 1условие нормировки, (следует из свойства ф.р.
	− ∞
Fξ (+∞ ) =		1) ;
3) кроме того,				x2
	P{ω : x1 < ξ (ω ) ≤ x2}			x2
	P{ω : x1 < ξ (ω ) ≤ x2}		= Fξ (x2 ) − Fξ (x1 ) = ∫ pξ (t)dt.
				x1
	Рассмотрим примеры непрерывных СВ:
1) СВ ξ (ω		) имеет равномерное распределение на отрезке [a,b] ,
если
			1	, x [a,b ]

			− a
		pξ (x) = b	− a	, рис. 6.5,
				[a,b ]
		0, x		[a,b ]

0, x < a,

F(x) = x a , a < x ≤ b, рис. 6.6,

ξb − a1, x > b;

2)СВ ξ (ω ) имеет показательное (экспоненциальное) распределение с параметром λ > 0, если−

pξ (x) =	0, x < 0	, рис. 6.7,
pξ (x) =		, рис. 6.7,
	λe− λx , x ≥	0

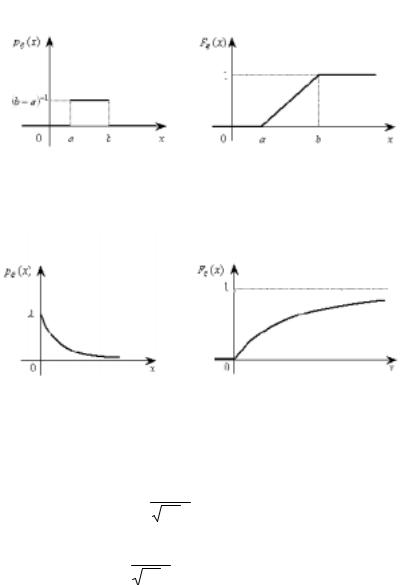
Рис. 6.5				Рис. 6.6
Fξ (x) =	0, x <		0	, рис. 6.8;
Fξ (x) =		− e− λx , x ≥ 0		, рис. 6.8;
	1	− e− λx , x ≥ 0

Рис. 6.7 Рис. 6.8

3) СВ ξ (ω

) имеет нормальное распределение с параметрами a, σ 2 ,

ξ (ω ) ~ N (a, σ 2 ) , если

e−

(x− a)2

pξ (x) =

2σ 2

, рис. 6.9,

2πσ

e−

(t− a)2

F (x)

−∫∞

2σ 2

dt,

рис. 6.10;

2πσ

4) СВ ξ (ω

) имеет распределение Коши с параметром a > 0 , если

(x) =

F (x) =

arctg

π(a2 +

x2 )

ô≥ 0

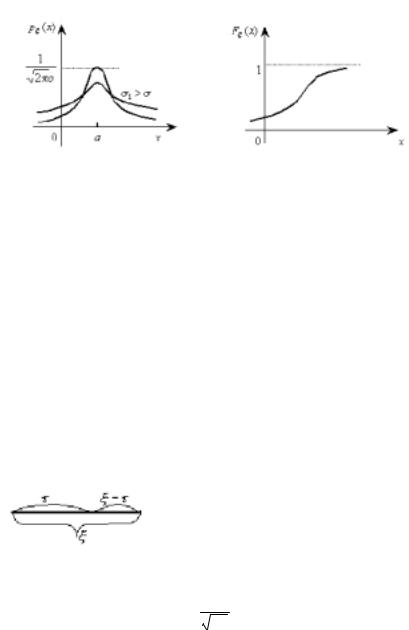
Рис. 6.9

Рис. 6.10

В частности, интервалы времени между соседними автомобилями на дорогах являются экспоненциально распределенными СВ с соответствующими параметрами λ > 0. Если ξ (ω ) – СВ, имеющая экспоненциальное распределение, то

P(ξ > x + τ / ξ > τ ) =			P(ξ > x + τ ,ξ > τ )		=	P(ξ > x + τ )	=
						P(ξ > τ )
			P(ξ > τ )
=	1− P(ξ ≤ x + τ )	=	1− 1− e− λ ( x+ τ )	= e− λx = 1− F (x) =
	1− P(ξ ≤ τ )		1− 1− e− λτ			ξ

= 1− P(ξ ≤ x) = P(ξ > x) P(ξ − τ ≤ x /ξ > τ ) = P(ξ ≤ x),
следовательно, см. рис. 6.11., СВ ξ − τ				имеет то же самое экспо-
ненциальное распределение, как и СВ ξ .

Нормальное распределение является наиболее широко применяемым на практике непрерывным распределением. В частности, оно применяется при моделировании броуновского движения, см. также п. 12.

Рис. 6.11	Пример 6.5. Проверим, что функция
	p(x) =	1	e−	x2
				2
		2π

является плотностью распределения вероятностей.

Решение. Ясно, что p(x) > 0. Нужно еще проверить условие нормировки. Это можно сделать несколькими способами:

а) пользуясь равенством	1		π ,	∞	t	k − 1	e	− t	dt –
а) пользуясь равенством	Г	=	π ,	где Г(k) = ∫	t		e		dt –
	2		∞∫	0
гамма-функция; б) возводя интеграл			∞∫	f (x)dx в квадрат и пере-

− ∞

ходя в двойном интеграле к полярным координатам.

Рассмотрим первый способ:

−

1 ∞

−

1 ∞

−

2 x2

∫ e

2π

− ∞

π 0

∞

−

2 e− t dt =

= 1.

π ∫0

Второй способ дает:

∞

−

x2 + y2

∫

f (x)dx

∫

dxdy =

2π

− ∞

= [x = r cos ϕ, y =

r sin ϕ]=

2π

∞

e−

∫

dϕ∫

rdr = 1,

2π

откуда следует тот же самый результат. Плотность p(x) называ-

ют плотностью стандартного нормального распределения, у которого a = 0, σ = 1.

III. СВ с сингулярными ф.р. Кроме дискретных и непрерывных СВ существуют другие СВ. В частности, кроме величин, которые на одних интервалах являются непрерывными, а

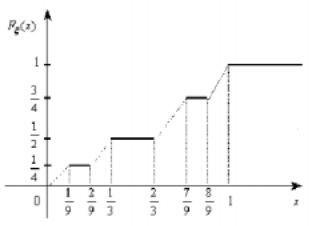
на других дискретными, существуют величины, не являющиеся ни на одном интервале ни дискретными, ни непрерывными. К таким СВ относятся, например, те, ф.р. которых непрерывные, но при этом возрастают только на множестве лебеговской меры нуль. В качестве примера можно привести величину, ф.р. которой – известная кривая Кантора. Кривая («лестница») Кантора строится следующим образом, рис. 6.12:

	1		1			2			1		1			2		3		7			8
Fξ (x) =		, x			,		,	Fξ (x) =		, x			,		, Fξ (x) =		, x			,		,
	2			3		3			4			9		9		4			9		9

...; и т. д. до бесконечности. В итоге ф.р. Fξ (x) оказывается определенной на счетном множестве интервалов, которые являются интервалами смежности некоторого нигде не плотного совершенного множества меры нуль. На этом множестве доопределим функцию Fξ (x) по непрерывности. Величина ξ с таким образом определенной ф.р. не дискретна, поскольку ее ф.р. непрерывна, но в то же время не абсолютно непрерывна, т.к. ее ф.р., не является интегралом от своей производной.

Рис. 6.12

Теорема Лебега. Любую ф.р. Fξ (x) однозначно можно представить в виде (разложение Лебега)

Fξ (x) = a1F1 (x) + a2 F2 (x) + a3 F3 (x),

где ai ≥ 0,i = 1,3,

a1 +

a2 + a3 =

1, F1 (x), F2 (x), F3 (x) – дискретная,

абсолютно непрерывная и сингулярная ф.р. соответственно.

Покажем, что если P{ω :ξ (ω ) = x} =

то x является точкой

непрерывности функции Fξ (x) . Действительно, ε > 0

P{ω : x − ε≤ ξ (ω ) ≤ x + ε} ≥ Fξ (x + ε) − Fξ (x − ε) ≥ 0.

Отсюда имеем

P{ω :ξ (ω

)

= x} = lim P{x − ε≤ ξ (ω

) ≤

x + ε} =

ε→

lim[Fξ (x +

ε) − Fξ (x −

ε) ]=

ε→

Справедливо и обратное утверждение: если x – точка непре-

рывности функции Fξ (x) , то P{ω :ξ (ω ) = x} =

0 .

Пусть ξ (ω )

– СВ с абсолютно непрерывной ф.р. Fξ (x) и

плотностью распределения pξ (x), y =

f (x)

– непрерывная возра-

стающая функция. Тогда для СВ η (ω

) =

f (ξ(ω ))

F ( y) = P{η ≤

P{ f (ξ ) ≤

}y = P{ξ ≤

− 1 ( y)} = F ( f − 1 ( y)),

и если, кроме того,

f (x) – дифференцируемая функция, то

( y) = p (f − 1 ( y))

df − 1 ( y)

Если же функция f (x) – убывающая, то

F ( y) = 1−

( f − 1 ( y)), p ( y) =

− p

( f − 1 ( y))

df − 1 ( y)

Пример 6.6. Случайная величина ξ

имеет показательное

распределение с параметром λ . Найти плотность распределения СВ η = ξ.

Решение:

Fη ( y) = P{ ξ ≤ y} = P{ξ ≤ y 2} = 1− e− λy2 , pη ( y) = Fη ' ( y) = 2λye− λy2 , y ≥ 0.

Пример 6.7. Пусть СВ ξ равномерно распределена на отрезке [0,1]. Найти ф.р. и плотности распределения СВ:

= ξ

= sin

πξ

а) η

б) η

ξ,

в) η

Решение:

а) F

(x) = P{ξ 2 ≤ x} = P{ξ ≤

x} =

x, 0 ≤ x ≤ 1,,

η1

(x) =

' (x) =

1 , 0 < x ≤ 1;

η1

2 x

б) Fη 2 (x) = P{ ξ ≤ x} = P{ξ ≤ x2} = x2 ,

(x) =

F '

(x) = 2x, 0 ≤ x ≤ 1;

η 2

в)

Fη 3 (x) =

2 πξ

πξ

P sin

≤

P sin

≤

arcsin

x ≤

P ξ ≤

x ,0 ≤

(x) = F '

(x)

,0 < x < 1.

η 3

x(1−

Пример 6.8. Найти плотности распределения СВ: а) η1 = ξ 3 ,

б)

η 2 =

, если известна плотность распределения СВ ξ .

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете Теория вероятностей и математическая статистика

#
03.10.2013193.14 Кб80сканирование0006.jpg
#
03.10.2013154.24 Кб44сканирование0007.jpg
#
03.10.2013139.75 Кб34сканирование0008.jpg
#
03.10.2013565.76 Кб152Твимс.doc
#
03.10.2013917.5 Кб102ТВиМСшпора(первоначальная).doc
#
03.10.2013850.21 Кб326Теория вероятностей в примерах и задачах.pdf
#
03.10.20131.28 Mб83тер вер.doc
#
03.10.2013198.13 Кб30Фото0058.jpg
#
03.10.2013200.44 Кб28Фото0059.jpg
#
03.10.20131.19 Mб78Ш_П_О_Р_А2.doc
#
03.10.20131.46 Mб75Шпора по теории для экзамена.docx