Образец выполнения конртольной работы .

Задание 1. Найти матрицу, обратную к матрице

Решение:

1. Вычислим определитель матрицы А

2. Обратная матрица А^-1 вычисляется по формуле , где А_ij^Т – транспонированная матрица, составленная из алгебраических дополнений.

а) Найдем алгебраические дополнения всех элементов матрицы

; ;

; ;

; ;

б) Составим матрицу алгебраических дополнений

в) Транспонируем матрицу А_ij и получим А_ij^Т

г) Вычисляем обратную матрицу

д) Для проверки умножим А^-1 на А, получим

Ответ: .

Задание 2. Дана система линейных алгебраических уравнений (СЛАУ)

.

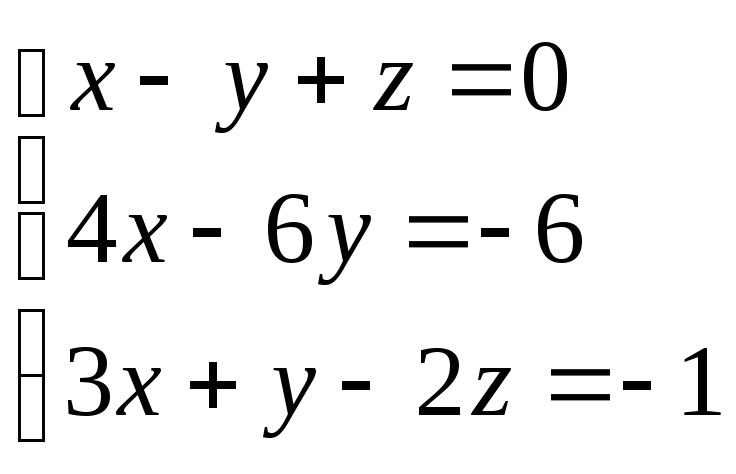Доказать ее совместимость и решить тремя способами:

1. методом Гаусса;

2. методом Крамера;

3. средствами матричного исчисления.

Решение:

1. Метод Гаусса заключается в последовательном исключении неизвестных и осуществляется в два этапа:

а) прямой ход заключается в приведении системы к ступенчатому (треугольному) виду; при этом, последнее уравнение системы имеет одну неизвестную; б) Обратный ход заключается в последовательном определении неизвестных из уравнений системы.

С помощью элементарных преобразований над строками расширенной матрицы системы сведем ее к треугольному виду. Если в процессе СЛАУ методом Гаусса какая-либо строка примет вид 0=0, это будет свидетельствовать о том, что СЛАУ имеет бесконечное множество решений, если же возникает строка 0 = const, то система несовместна.

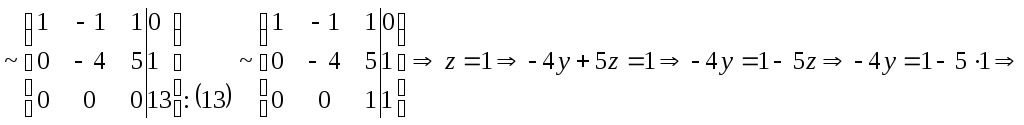
. Ответ: (0,1,1).

2. Методом Крамера

При СЛАУ совместна и, причем, она имеет единственное решение, которое может быть найдено по формулам Крамера, где ∆ - определитель матрицы А системы, а ∆_х, ∆_у, ∆_z – определители для неизвестных (х,у,z), полученные заменой соответствующего столбца, составленного из коэффициентов при неизвестных, на столбец свободных членов.

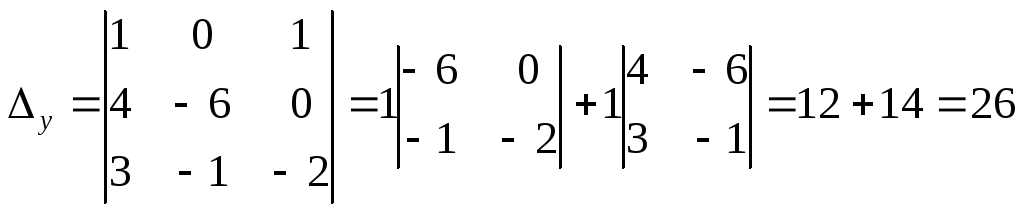
. Ответ: (0,1,1).

3. средствами матричного исчисления

СЛАУ удобно записать в матричной форме А·Х=С, где А – матрица системы, Х – столбец неизвестных членов, С – столбец свободных членов.

Из матричного уравнения следует Х = А^-1С, (*) где А^-1 – обратная матрица, которая вычисляется по формуле , где А_ij^Т – транспонированная матрица, составленная из алгебраических дополнений.

Вычислим определитель матрицы А (смотрите выше)

а) Найдем алгебраические дополнения всех элементов матрицы

; ;

; ;

; ;

б) Составим матрицу алгебраических дополнений

в) Транспонируем матрицу А_ij и получим А_ij^Т

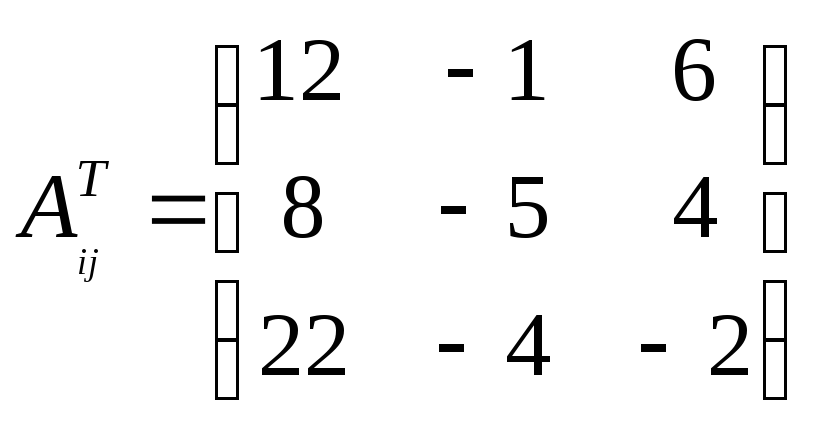
г) Вычисляем обратную матрицу

Согласно формуле (*) столбец решений

.

Таким образом, СЛАУ: х = 0, у = 1, z = 1, что подтверждается в ходе проверки (подстановки полученных значений в каждое уравнение системы).

Задание 3.

Даны вершины треугольника АВС: А(1;-1;2), B(5;-6;2), С(1;3;-1). Найти длину его высоты, опущенной из вершины В на сторону АС.

Решение: Площадь S треугольника АВС равна половине площади параллелограмма, построенного на векторах и, то есть. Имеем:,. Тогда векторное произведение этих векторов равно.

(*).

Известно, что площадь треугольника равна (**).

Приравняем равенства (*) и (**) и определим высоту h

. Ответ: h = 5.

Задание 4.

Даны координаты вершин пирамиды А₁А₂А₃А₄

А₁ (2; -1; 1), А₂ (5; 5; 4), А₃ (3; 2; 3), А₄ (4; 1; 3).

Найти:

1. длину ребер A₁A₂; A₁A₃; A₁A₄;

2. угол между ребрами: A₁A₂ и A₁A₄;

3. площадь грани A₁A₂А₃;

4. объем пирамиды;

5. длину высоты, опущенной из вершины А₄ на грань A₁A₂А₃.

Решение:

1. ,

,

,

2. Пусть α угол между ребрами A₁A₂ и A₁A₄. Скалярное произведение векторов изапишется в следующем виде:

.

3. Площадь грани A₁A₂А₃ будем вычислять, исходя из геометрического смысла векторного произведения векторов. Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах. Площадь треугольника A₁A₂А₃ равна .

.

.

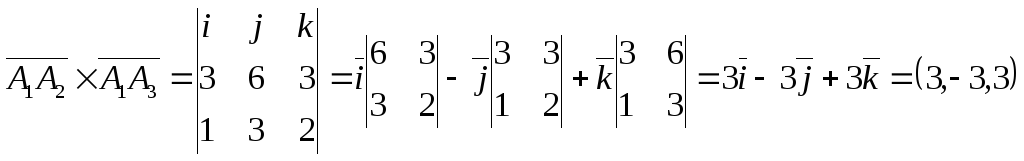4. Объем пирамиды численно равен 1/6 модуля смешанного произведения векторов, образующих данную пирамиду, то есть , и .

.

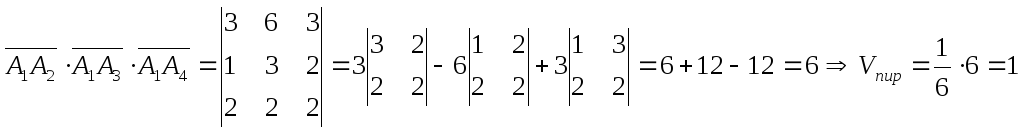5. Известно, что 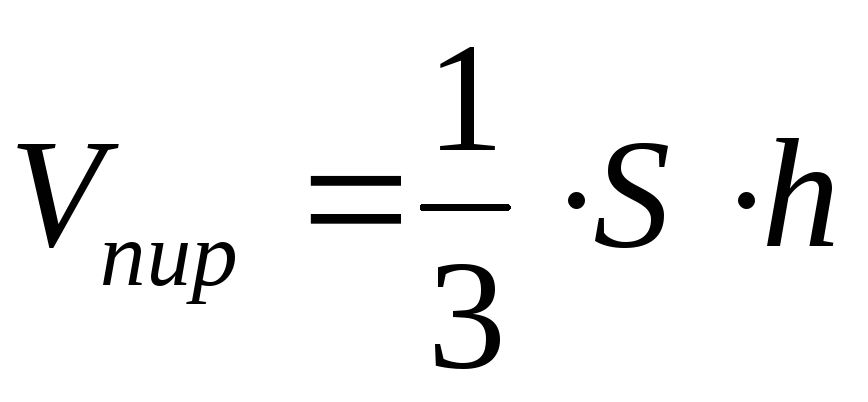, гдеS – площадь основания (грань A₁A₂А₃) пирамиды, а h – высота пирамиды, опущенной из вершины А₄ на грань A₁A₂А₃. .

Задание 5.

а) Найти острый угол между двумя плоскостями .

Решение: Угол между двумя плоскостями иравен углу между их нормальными векторамиии определяется по формуле

.

Из формулы (*) получим, если учесть, что на основании уравнения (I) А₁ = 5; В₁ = 3; С₁ = 4, а из (II) А₂ = 3; В₂ = -4; С₂ = -2,

. В формуле (*) следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями.

б) Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей Р₁, Р₂ и точку М(2,-1,3).

Решение: Две пересекающиеся плоскости Р₁ и Р₂ определяют (задают) пучок плоскостей, уравнение которого имеет вид 5x–3y+4z–4+t(3x–4y–2z+5)=0, где t – параметр. Все плоскости этого пучка проходят через прямую пересечения плоскостей Р₁ и Р₂ (ось пучка). Из множества плоскостей пучка выбираем ту (определяем значение t), которая проходит через точку М: значение t должно быть таким, чтобы координаты точки М удовлетворяли уравнению

.

Уравнение искомой плоскости

.

Задание 6. Даны уравнения высот треугольника 2х – 3у + 1 = 0 и х + у = 0 и координаты одной из его вершин А(1;2). Найти уравнения сторон треугольника.

Решение: Точка А(1;2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям:

2·1 - 3·2 + 1 ≠ 0 и 1 + 2 ≠ 0. Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника В и С. Назовем их СД и ВЕ, ,. Пусть высота СД имеет уравнение х + у = 0, а высота ВЕ имеет уравнение 2х – 3у + 1 = 0.

I способ. Так как , то уравнение АС мы найдем из уравнения семейства прямых, перпендикулярных ВЕ, приняв во внимание, что искомая прямая проходит через данную точку А(1;2).

Если две прямые перпендикулярны, то выполняется условие, то есть коэффициенты при х и у меняются местами, а также изменяется знак при у.

1. Уравнение стороны АС

2. Уравнение стороны АВ

3. Уравнение стороны ВС

Сначала следует найти координаты точек В и С, как точек пересечения прямых ВЕ и АВ и прямых СД и АС, соответственно.

Теперь найдем уравнение ВС, воспользовавшись уравнение прямой, проходящей через две точки В(-2;-1) и С(7;-7).

II способ. Если две прямые заданы уравнениями и, то условия перпендикулярности двух прямых имеет вид.

1. Уравнение стороны АС ()

Определим угловой коэффициент высоты ВЕ. Преобразуем уравнение высоты ВЕ:.

Уравнение прямой, проходящей через данную точку А(х₁;у₁) в данном направлении, определяемом угловым коэффициентом, (**).

Точка А(1;2) принадлежит прямой АС, поэтому подставим ее координаты в уравнение (**). .

2. Уравнение стороны АВ ()

Угловой коэффициент высоты СД, имеющей вид, равен.

3. Уравнение стороны ВС рассмотрено выше.

Задание 7. Найти уравнение касательной к параболе у² = 4х, проведенной из точки А(-2;-1).

Решение: Уравнение прямой будем искать в виде . Так как точка А принадлежит искомой касательной, подставляя ее координаты в уравнение (*), получим тождество. Далее, прямая (*) и парабола у² = 4х имеют единственную общую точку (касаются). Следовательно, система уравнений имеет единственное решение. Решаем ее относительно х и у. Это можно сделать различными способами, например, возвести правую и левую части первого уравнения в квадрат и подставить в левую часть полученного равенства вместо у² его выражение из второго уравнения. Получим . Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Таким образом,. Теперь для параметровk и b прямой (*) имеем два условия: (**) и (***). Следовательно, искомые значения параметров находятся как решения системы из этих условий:

. Подстановкой вместо b в первое уравнение его выражения из второго, получим , откуда находим, что. Система имеет два решения:. Следовательно, две прямые удовлетворяют условиям задачи. Их уравнения:.

Литература:

1. Высшая математика для экономистов. Под редакцией проф. Н.Ш. Кремера.

2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики М.: Наука, 1975 г.

3. Сборник задач и упражнений по высшей математике. А.В.Кузнецов и др. – Минск: Высш. Школа, 1994 г.

4. Сборник задач по курсу математического анализа. Г.Н.Берман – М.: Государственное издательство физико-математической литературы, 1970

5. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. Ч. 3. – М.: Изд-во «Высшая школа», 1971.

6. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М.: Высшая школа, 1982

7. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. В 2-х частях. – М.: Айрис Пресс, 2004.

8. Каплан И.А., Пустынников В.И. Практикум по высшей математике. В 2-х томах. – М.: ЭКСМО, 2006.

9. Арутюнов Ю.С., Полозков А.П., Полозков Д.П. Высшая математика: методические указания и контрольные задания (с программой) для студентов-заочников инженерно-технических специальностей высших учебных заведений. – М.: Высшая школа, 1985. – 144 с.

10. Баранова Е.С., Васильева Н.В., Федотов В.П. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие. – СПб.: Питер, 2008. – 320 с.