2. Дифференциальное исчисление
-
Производная функции F(x)=ln3x равна:
-
3хln3
-
3x
-
-
Для функции
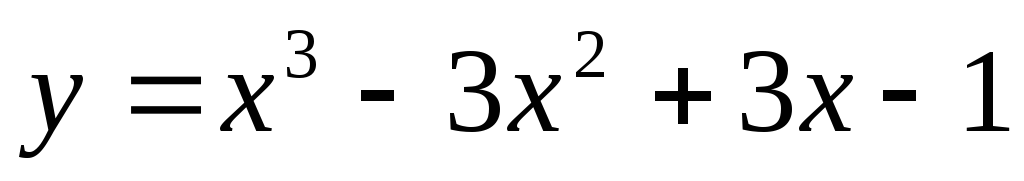 точка М(1, 0) является точкой
точка М(1, 0) является точкой
-
максимума
-
перегиба
-
минимума
-
разрыва
-
-
Функция f (x) называется нечетной, для всех x из области определения, если
-
f(-x) = f(x)
-
f(x-3) = -f(x)
-
f(-x) = -f(x)
-
f(-3x) = -f(x)
-
-
Для функции
 точка М(-2, 0) является точкой
точка М(-2, 0) является точкой
-
максимума
-
минимума
-
перегиба
-
разрыва
-
-
Вертикальной асимптотой графика функции
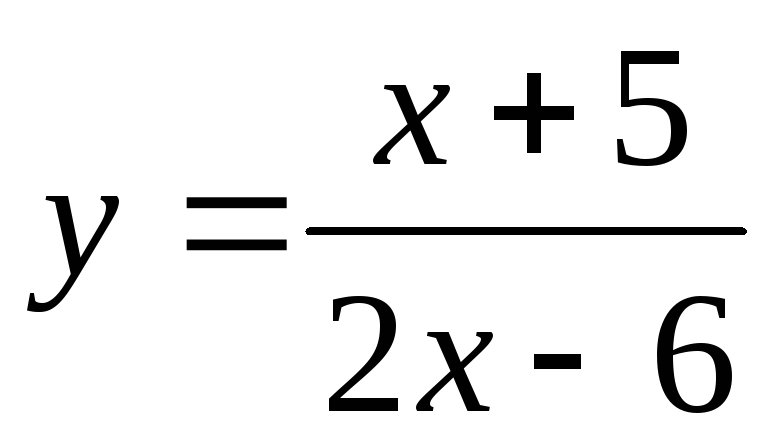 является прямая:
является прямая:-
х = 2
-
х = - 3
-
х = - 5
-
х = 3
-
-
Стационарной точкой функции
 является
точка
является
точка
 в которой
в которой
-
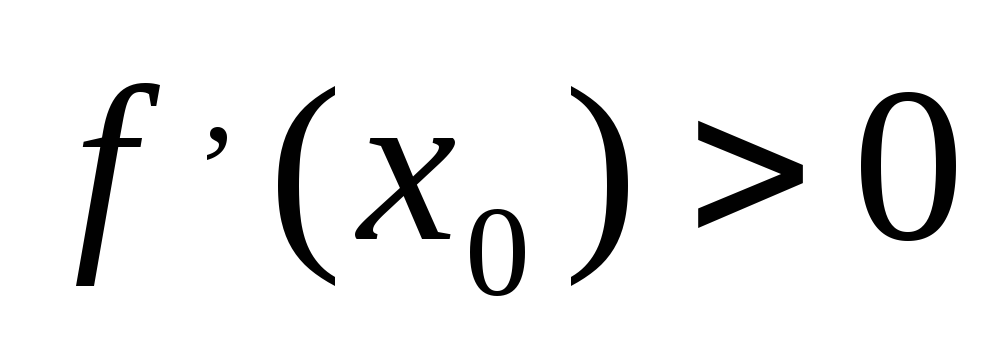
-

-
 не существует
не существует -

-
Для функции
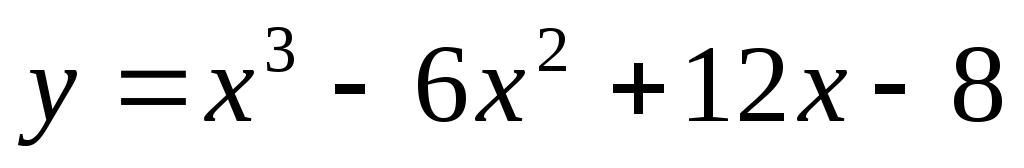 точка М(2, 0) является точкой
точка М(2, 0) является точкой
|
|
|
|
|
|
|
-
Производная функции F(x) = cos(3 - 4x) равна
-
F’ (x) = 4cos(3 - 4x)
-
F’ (x) = 4xsin(3 - 4x)
-
F’ (x) = 4xcos(3 - 4x)
-
F’ (x) = 4sin(3 - 4x)
-
Для функции
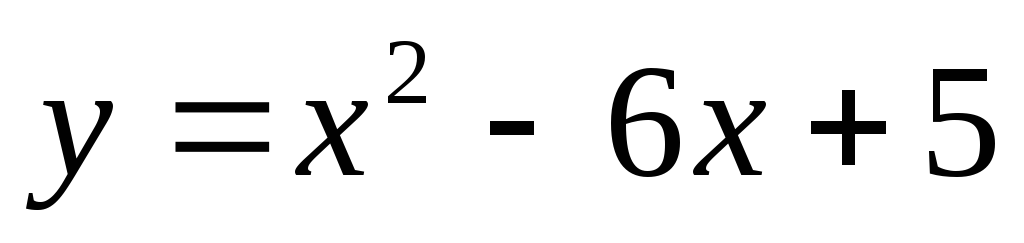 точка М(3, - 4) является точкой
точка М(3, - 4) является точкой
-
минимума
-
максимума
-
перегиба
-
разрыва
-
Среди перечисленных функций 1) y = cos2x; 2) y = 2x + 5; 3) y = x3 - 1; 4) y = 6x+2 ; 5) y = -x7 степенными являются только:
-
1; 5
-
3; 5
-
2; 4
-
3; 4
-
Функция называется периодической, если существует такое постоянное число Т 0, что для любого x из области определения выполняется равенство
-
Tf(x) = f(x)
-
f(Tx) = f(x)
-
T + f(x) = f(x)
-
f(x T) = f(x)
-
Стационарными точками функции
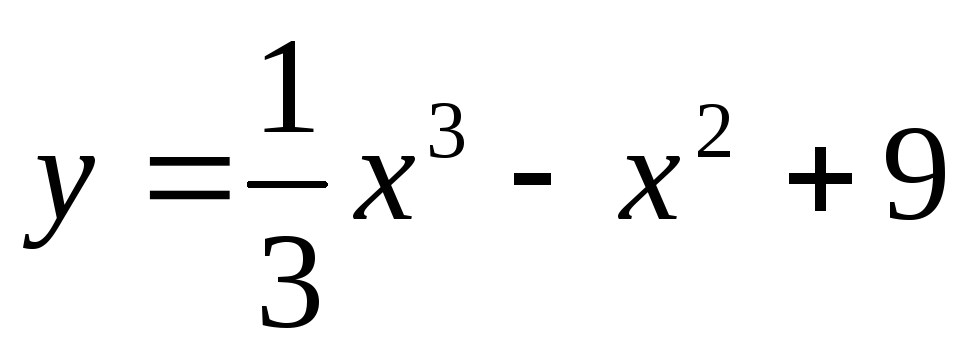 являются точки
являются точки
-
Среди перечисленных функций 1) y = 2sinx; 2) y = 1/3 tg x/2; 3)
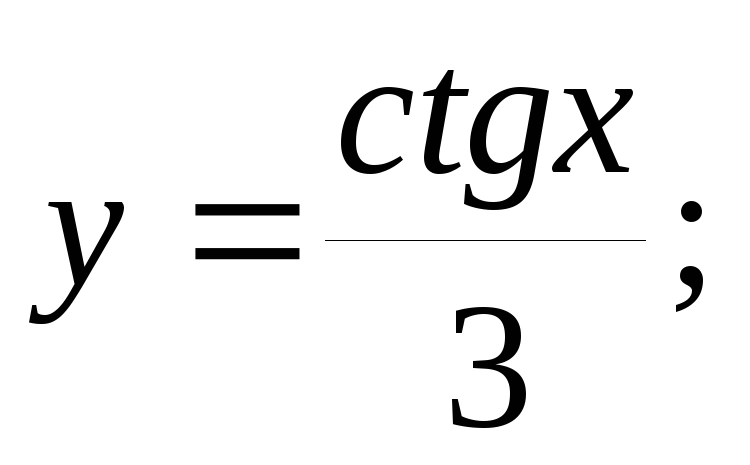 4) y
= cos
x/4;
5) y
= 3sin2
x/4
ограниченными функциями являются
4) y
= cos
x/4;
5) y
= 3sin2
x/4
ограниченными функциями являются
-
1; 2; 3
-
1; 4; 5
-
2; 3; 4
-
3; 4; 5
-
Производная функции
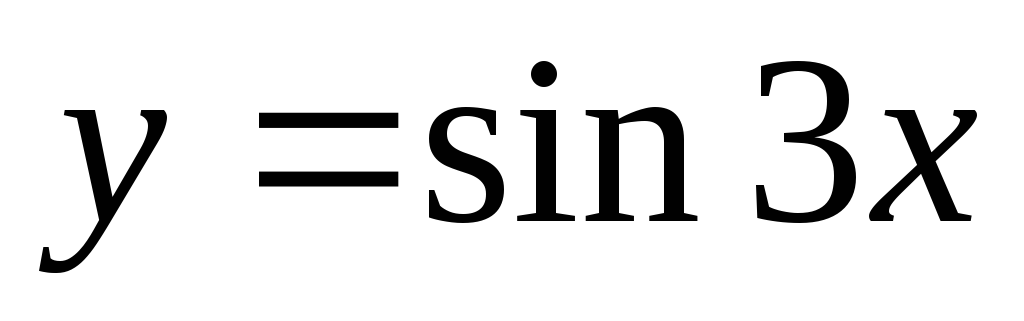 равна
равна
-
–3cos3x
-
3cosx
-
3cos3x
-
cos3x
-
Вертикальной асимптотой графика функции
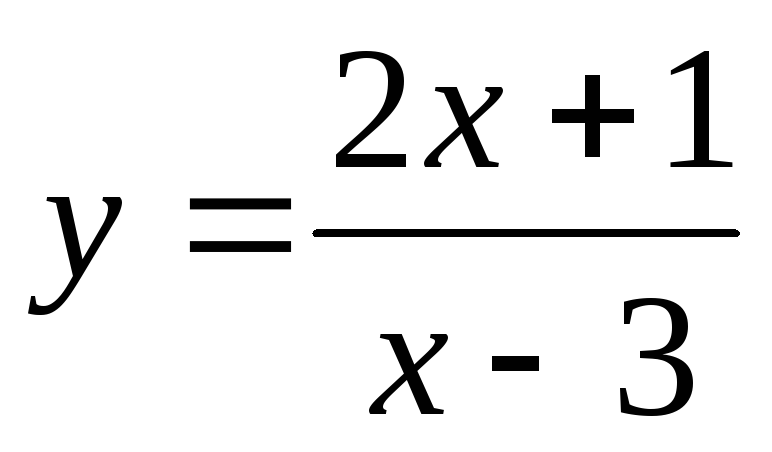 является прямая
является прямая
-
Производная
 для функции
для функции
 равна
равна
-
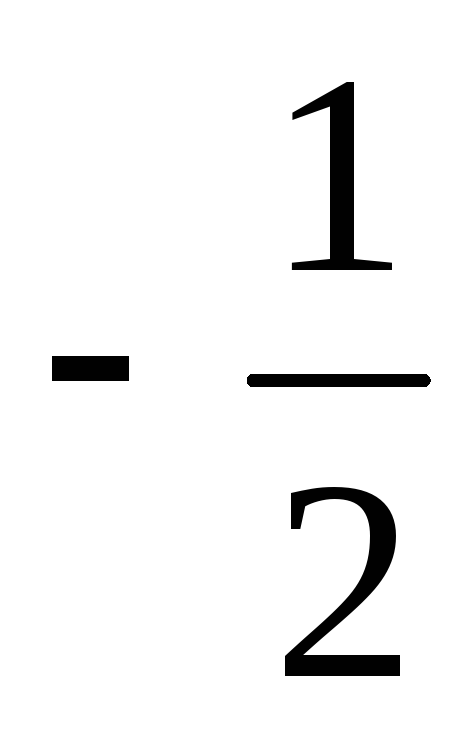
-
2
-
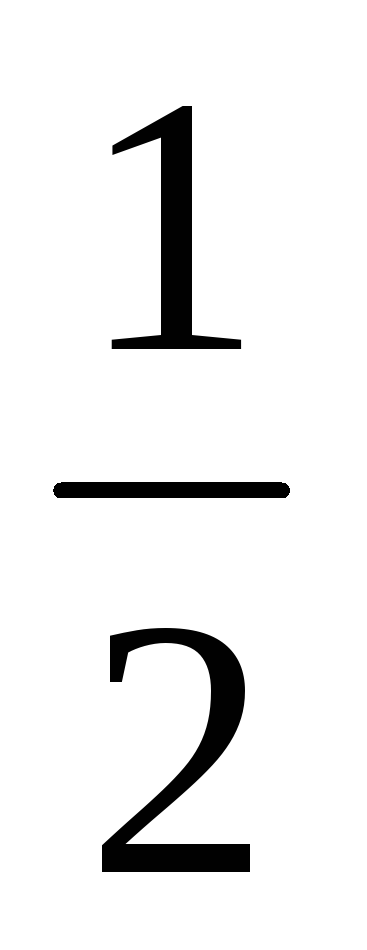
-
1
-
Среди перечисленных функций 1) y = 5x +2; 2) y = tg3 x/2; 3) y = 2x5; 4) y = 3x-2; 5) y = x-1 показательными функциями являются только:
-
1; 5
-
2; 3
-
1; 4
-
3; 4
-
График четной функции симметричен относительно
-
оси абсцисс
-
оси ординат
-
начала координат
-
биссектрисы I координатного угла
-
Точка с абсциссой
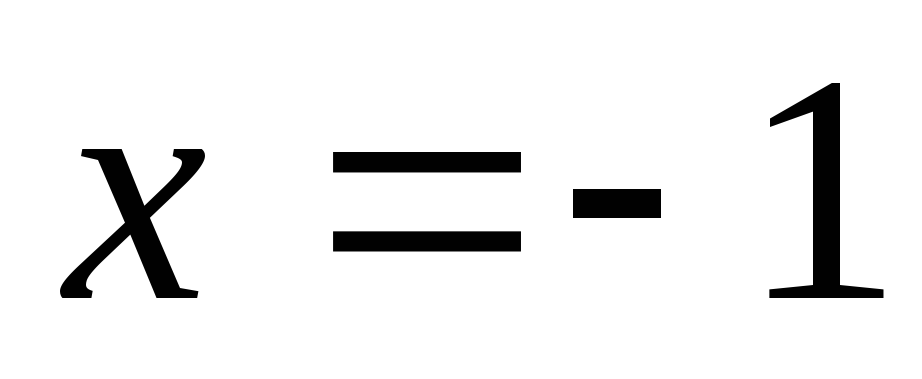 для функции
для функции
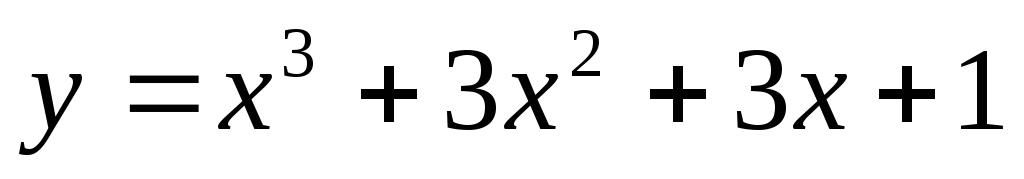 является точкой
является точкой
-
максимума
-
перегиба
-
минимума
-
разрыва
-
Точкой перегиба функции
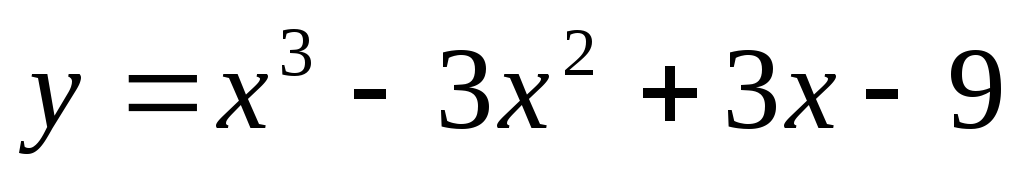 является точка с абсциссой
является точка с абсциссой
-
Производная функции
 равна
равна
-
е-х
-
ех
-
–е-х
-

-
Точка
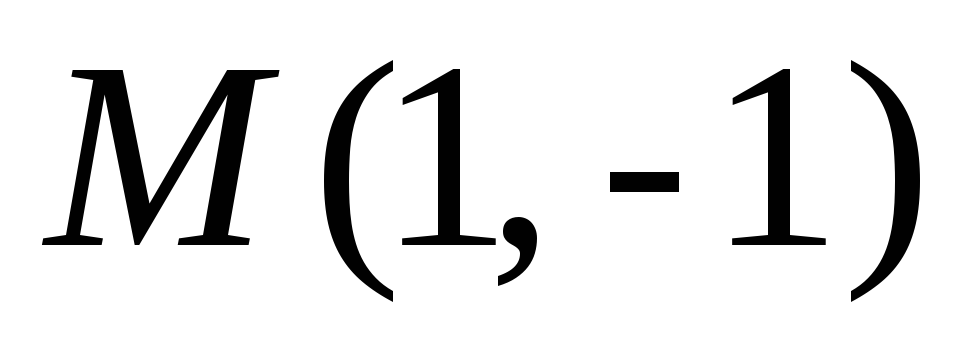 для функции
для функции
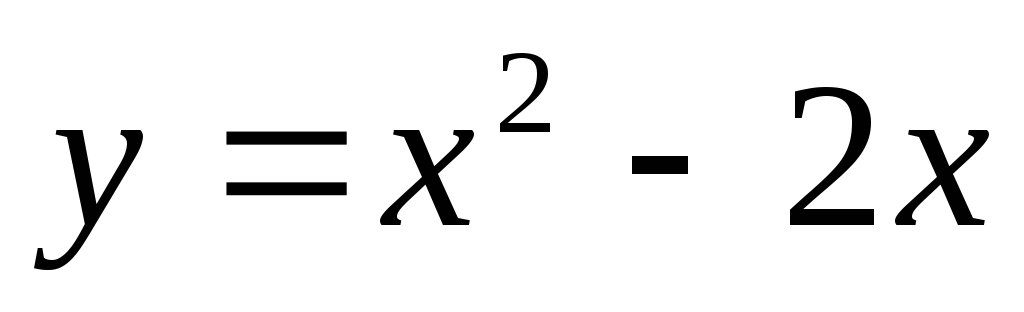 является точкой
является точкой
-
максимума
-
перегиба
-
разрыва
-
минимума
-
Функция
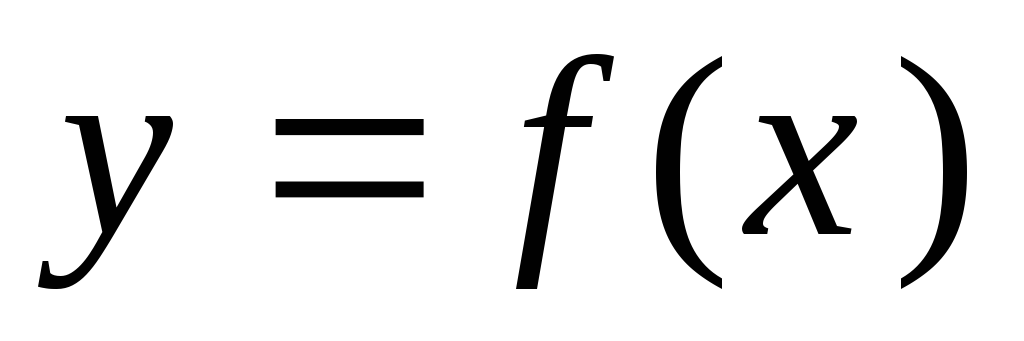 является
возрастающей на интервале, если на
этом интервале
является
возрастающей на интервале, если на
этом интервале
-
Функция
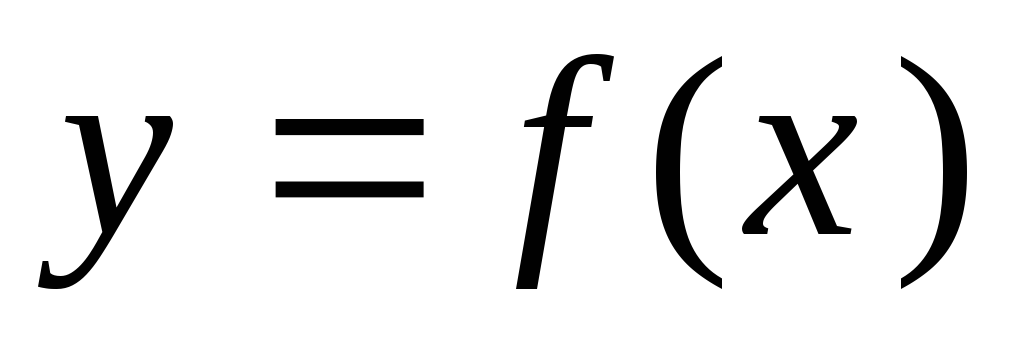 является убывающей на интервале, если
на этом интервале
является убывающей на интервале, если
на этом интервале
-
Предел отношения приращения функции y = f(x0+x) - f(x0) к приращению аргумента x при стремлении x к нулю называется
-
производной функции f(x)
-
первым замечательным пределом
-
вторым замечательным пределом
-
первообразной функцией f(x)
-
Производная функции
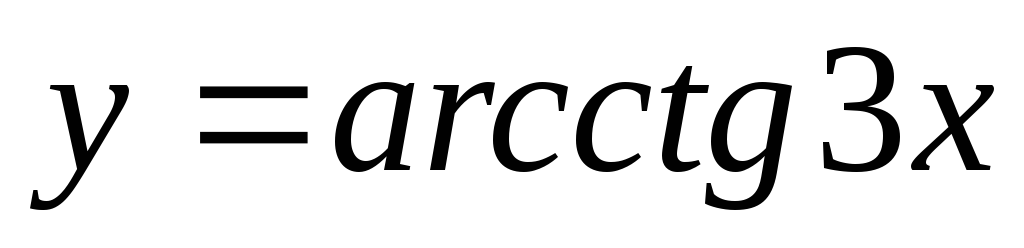 равна
равна
-
Среди перечисленных функций: 1) y = 1/x; 2) y = 5x + 1; 3) y = x2/4 ; 4) y = x3; 5) y = -5x2 ; - убывают на промежутке (-2; 0) только:
-
2; 4
-
1; 3
-
1; 5
-
3; 5
-
Вертикальной асимптотой графика функции
 является прямая
является прямая
-
х = 1
-
х = 4
-
х = -1
-
y = 0
-
Производная функции
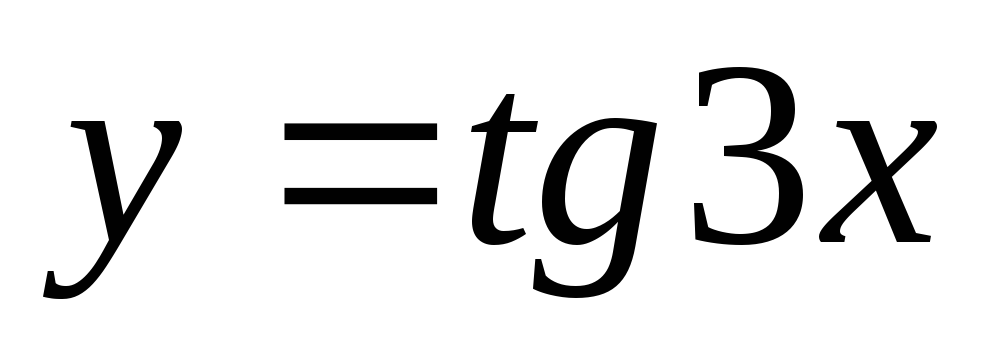 равна
равна
-
Производная для функции
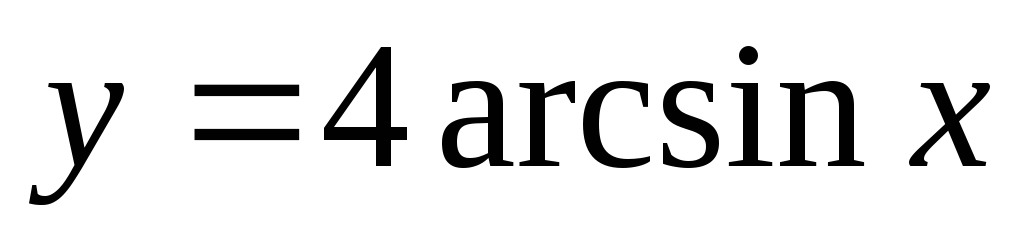 в точке
в точке
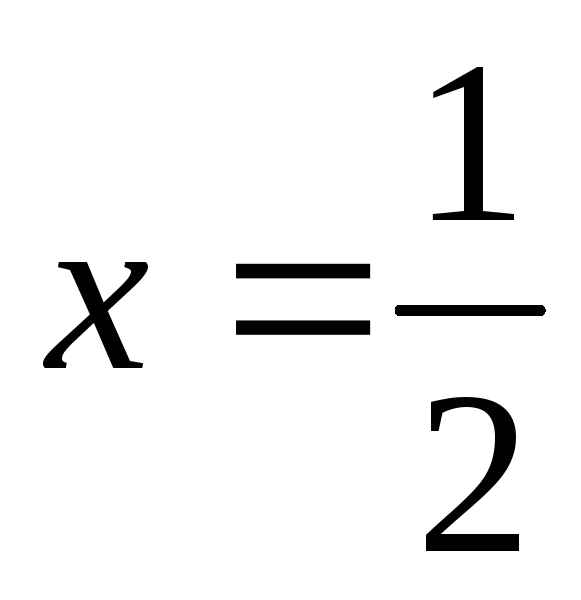 равна
равна
|
|
|
|
|
|
-
График нечетной функции симметричен относительно
-
начала координат
-
оси ординат
-
оси абсцисс
-
биссектрисы III координатного угла
-
Производная функция
 при
при
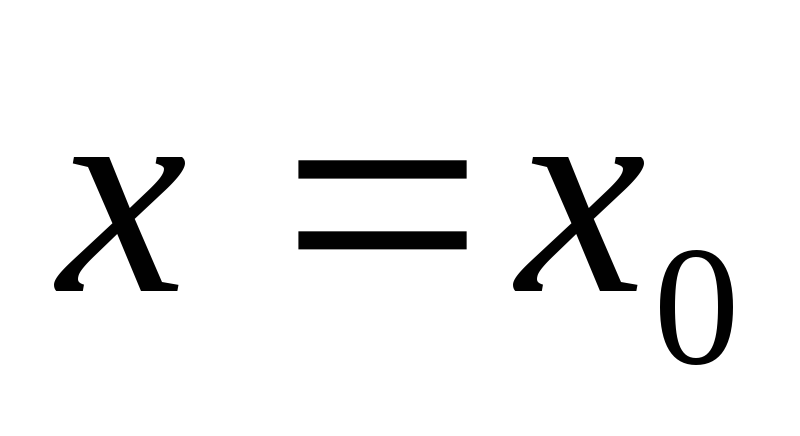 равна
равна
-
тангенсу угла наклона нормали, проведенной к кривой
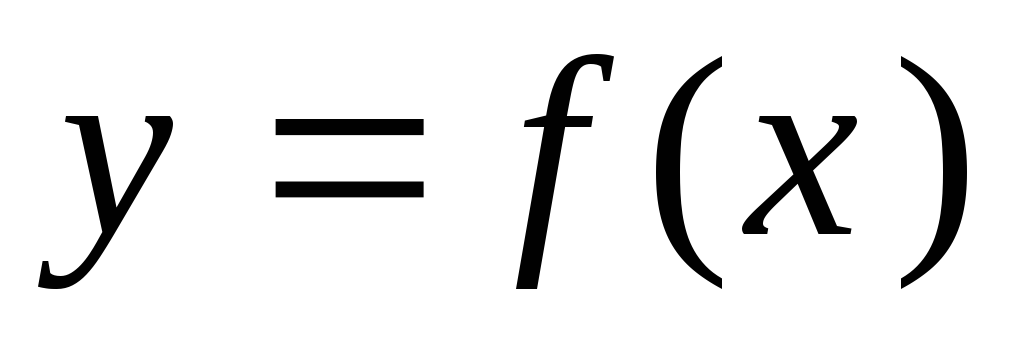 в
точке
в
точке
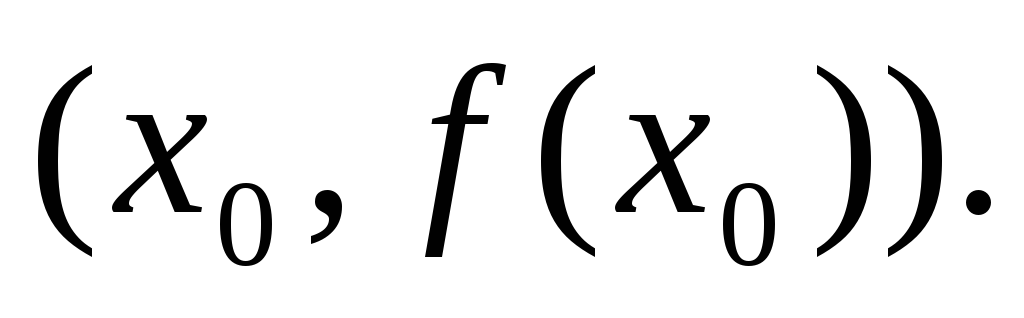
-
тангенсу угла наклона касательной, проведенной к кривой
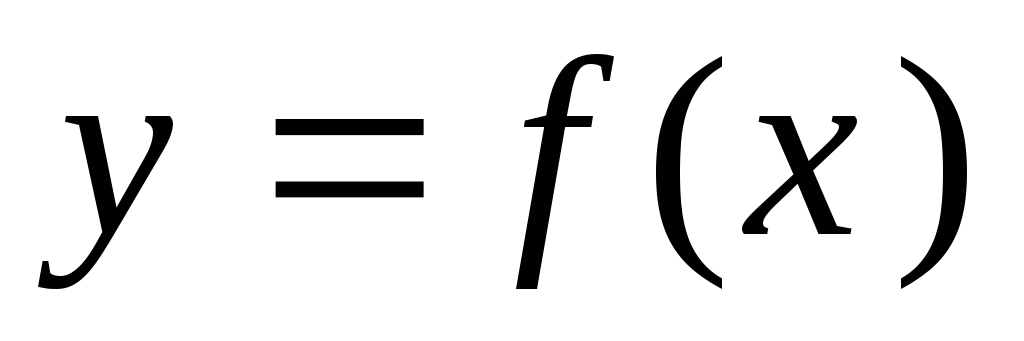 в точке
в точке

-
тангенсу угла, который образует кривая
 с
осью ОХ
с
осью ОХ -
тангенсу угла, который образует кривая
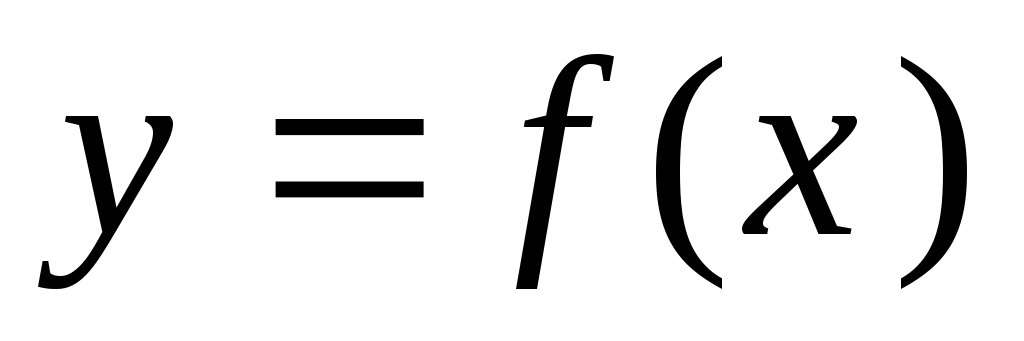 с
осью OY
с
осью OY
-
Точкой перегиба функции
 является
точка при переходе через которую
является
точка при переходе через которую
-
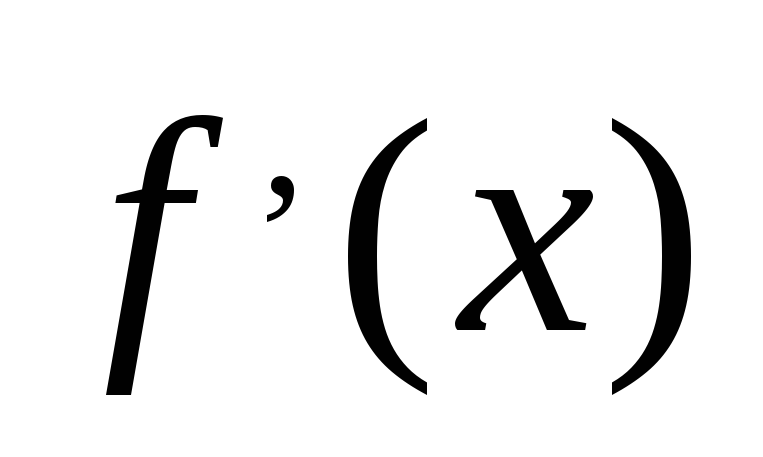 меняет знак
меняет знак -
 сохраняет знак
сохраняет знак
-
 сохраняет знак
сохраняет знак -
 меняет знак
меняет знак
-
Производная функции
 имеет
вид…
имеет
вид…
-
Производная функции
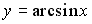 в точке
в точке
 равна …
равна …
-
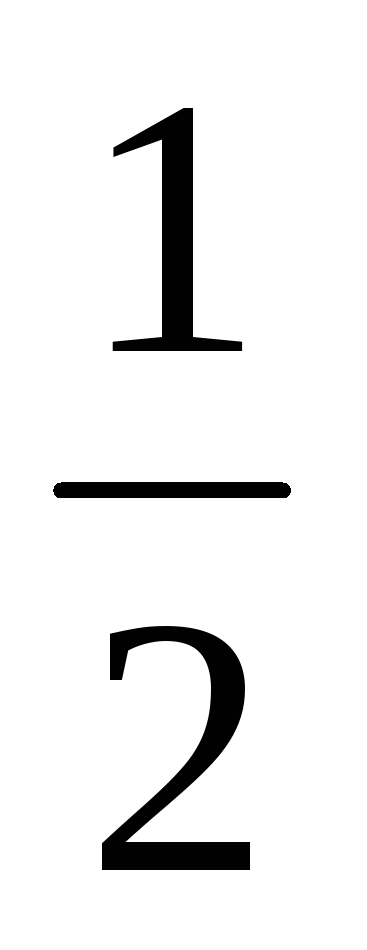
-
–1
-
1
-

-
Установите соответствие между функциями и их производными.
![]()
![]()
![]()
-
Вторая производная функции
 равна
…
равна
…
Угловой
коэффициент касательной к графику
функции
![]() в точке
в точке
![]() равен …-7
равен …-7
-
1
-
-1
-
-6
-
Расположите функции, определенные на всей числовой прямой, знаки производных которых указаны на рисунках, по возрастанию количества точек максимума.
-
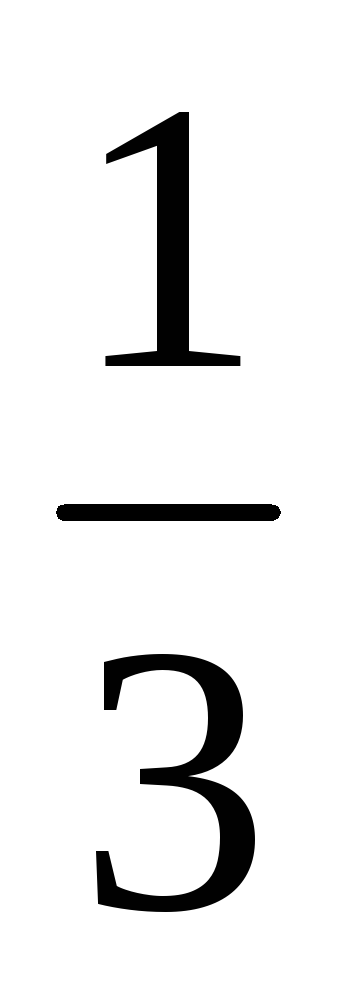
Абсциссой точки перегиба графика функции
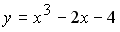 является …
является …
-
-
-6
-
6
-
0
-
Дана функция
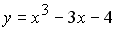 Установите соответствие между
производными функции в соответствующих
точках и их значениями.
Установите соответствие между
производными функции в соответствующих
точках и их значениями.
![]()
![]()
![]()
-
9
-
-3
-
0
-
Скорость материальной точки, движущейся прямолинейно, равна
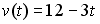 тогда путь, пройденный точкой от начала
отсчета времени до остановки, равен …
тогда путь, пройденный точкой от начала
отсчета времени до остановки, равен …
-
Дифференциал функции
 имеет
вид…
имеет
вид…