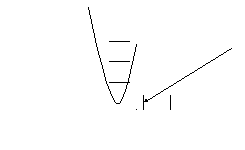2. Методические указания

§ 1. Предел функции

Определение. Число А называется пределом функции y = f(x) в точке а (или при х а (стремящимся к а)), если для любой сходящейся к а последовательности х₁, х₂, х₃,…, х_n, … отличных от а, соответствующая последовательность значений функции f(x₁), f(x₂), f(x₃), …, f(x_n), … сходится к числу А.

Обозначение: lim f(x) = A.

xa

A может быть как конечным, так и бесконечным числом.

Если конечны, то

; (1.1)

(1.2)

при любом постоянном с;

; (1.3)

,

если .

Вычисления пределов отношений двух функций, когда числитель и знаменатель одновременно стремятся к 0 или ∞, называется раскрытием неопределенностей. Неопределенности символически изображаются или, для их раскрытия применяются различные методы.

Пример 1. Вычислить пределы функций.

1) при а) х₀=2; б) х₀=1; в) х₀=∞.

2)

Решение.

1. а) нужно найти 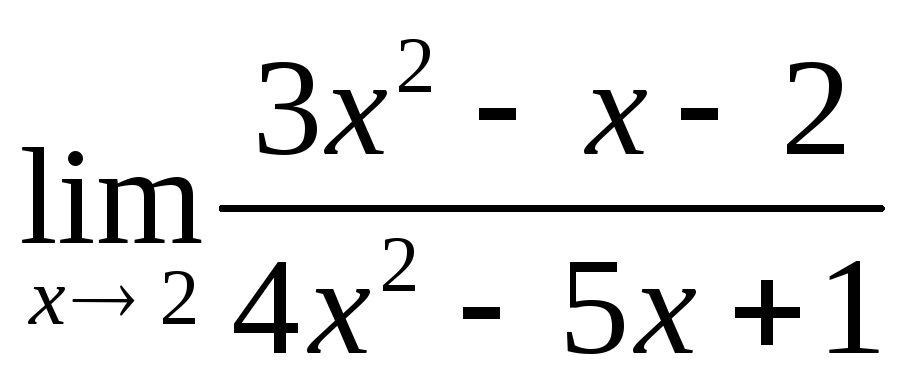. Найдем предел знаменателя:,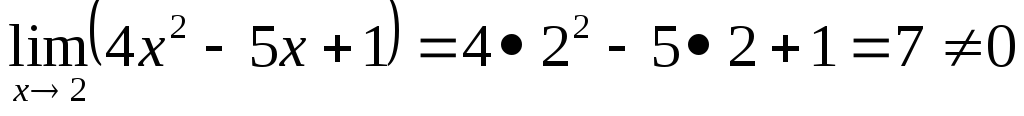

следовательно ,

б) нужно найти . Найдем предел знаменателя:.

Найдем предел числителя: .

Следовательно, х = 1 является общим корнем числителя и знаменателя, т. е. нужно раскрыть неопределенность вида . Для раскрытия неопределенности разложим числитель и знаменатель на множители и общий множитель сократим:

3х²-х-2 = (х-1) (3х+2),

4х²-5х+1 = (х-1) (4х-1),

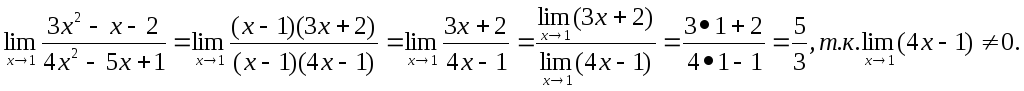
в) нужно найти . Прих∞числитель и знаменатель стремятся к ∞, т. е. имеем неопределенность вида вида . Для раскрытия неопределенности разделим числитель и знаменатель дроби нах², при этом дробь не изменится. Получим

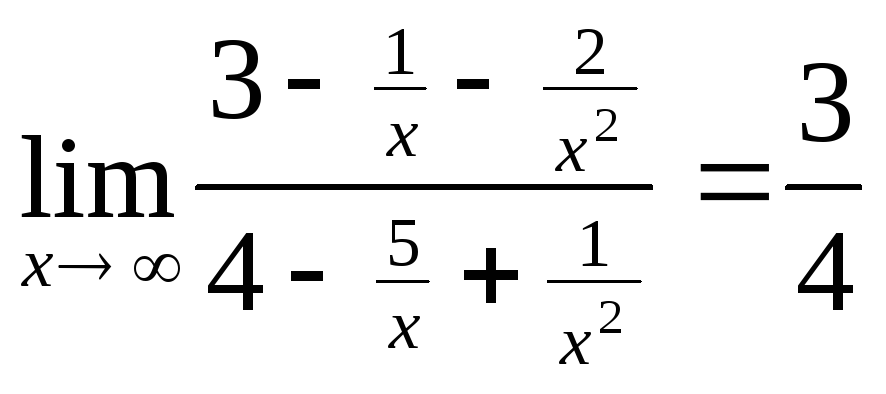= ,т. к.

^{= 0;} = 0;4 -= 40.

1. нужно найти 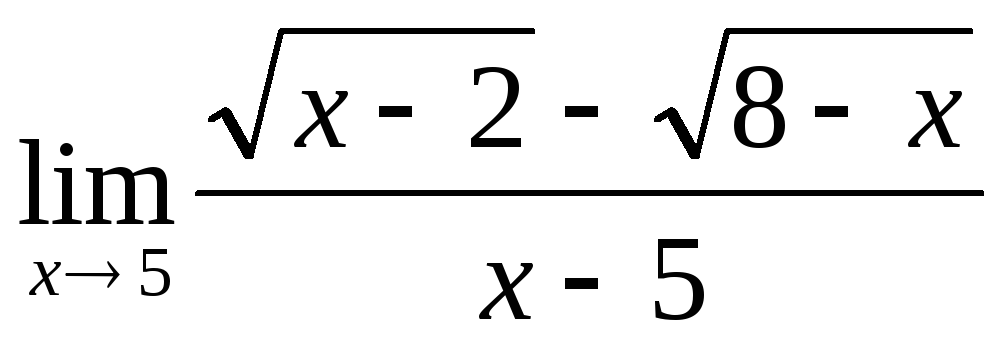. Найдем предел знаменателя:

(х-5)=0

Найдем предел числителя:

() == 0,

т.е. нужно раскрыть неопределенность вида . Для этого умножим числитель и знаменатель дроби на, дробь при этом не изменится, получим:

=

=

= ==

=

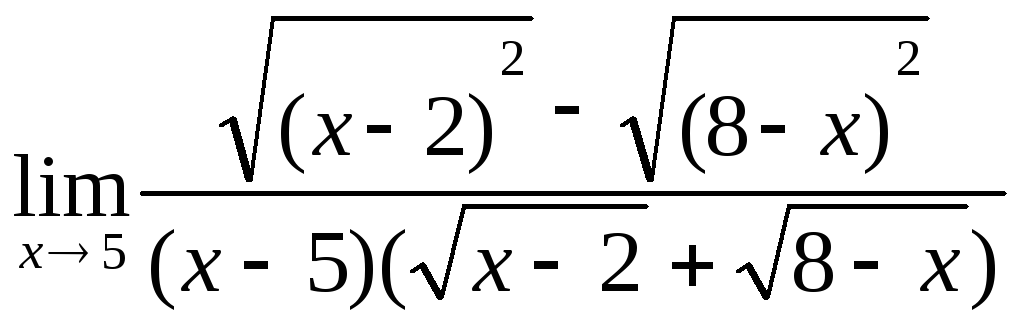
§ 2. Непрерывность функции.

Определение. Функция y = ƒ(x) называется непрерывной в точке х = а, если существует предел функции в этой точке, который равен значению функции в точке, т.е.

.

Точка x = а называется точкой разрыва функции y = ƒ(x), если эта функция определена в некоторой окрестности точки x = a, но в самой точке

x = а не удовлетворяет условию непрерывности.

Точки разрыва функции делятся на два типа. К точкам разрыва первого рода относятся такие точки, в которых существуют конечные односторонние

пределы (левый предел) и (правый предел), при этом

≠

К точкам разрыва второго рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.

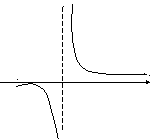
Пример 2.

1) Дана функция y = . Найти точки разрыва и исследовать их характер. Построить схематично график функции в окрестностях точек разрыва.

Решение.

Функция y = определена при всех значениях х, кроме х = - 3. Так как эта функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков (- ∞;-3 ) и (-3;+ ∞).

Следовательно, единственной точкой разрыва является точка х = -3 (функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней неопределена).

Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке разрыва Х = - 3:= + ∞; = - ∞; Следовательно, при х = - 3 функция у = имеет бесконечный разрыв (рис. 1); х = - 3 есть точка разрыва второго рода.

Рис. 1

Пример 3. Дана функция .

Найти ее точки разрыва и исследовать их характер. Построить чертеж.

Решение.

Числовая ось, являющаяся областью определения функции, разбить на два промежутка (-,1) и (1,+), в каждом из которых исследуемая функция является элементарной и непрерывной.

Исследуем нашу функцию на непрерывность при x = 1.

Вычислим односторонние пределы при х стремящимся к единице слева и справа:

Следовательно, при х = 1 имеется разрыв первого рода (скачок функции в точке).

Вычислим значение функции при :

Y(1) =

Значит, наша функция непрерывна слева.

Таким образом, исследуемая функция непрерывна на всей числовой оси за исключением точки , в которой она терпит разрыв 1 ряда.

Построим чертеж.

Производная

Основные правила дифференцирования:

;

при C=const;

;

.

Пример 4. Найти производные заданных функций.

а) б)

в) г)

Решение.

а)

Используем формулы:

при

Тогда

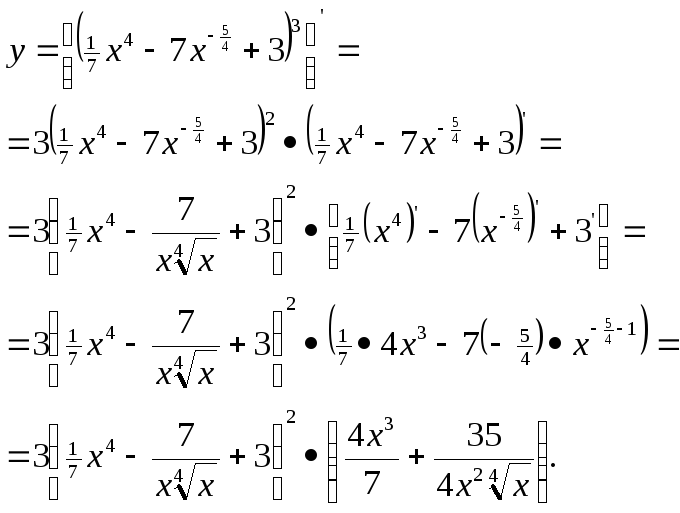
б)

Преобразуем функцию y по свойствам логарифмов:

In a – In b;InIn a.

Для нахождения производной используем формулы:

(In U)’ = (CU)’ = CU’;

C’= 0; X’ = 1;

( U + V – W)’ = U’ + V’ – W’

Получим:

у’ = In In=In(1+7Х)- In(1-7Х);

у’= [ In (1+ 7X) – In(1-7X)]= =

=

=

в) у = 2 arctg .

Используем формулы:

(arctg U)’ = при U = ;

(U)’⁼ nUU; (СU)= С U;

(U+V)’= U’ = V’; C’ = 0;