Содержание

ВВЕДЕНИЕ ……..5

1 Анализ технического задания 7

2 Теоретические основы криптографического алгоритма Блюма–Блюма–Шуба и линейного конгруэнтного метод 10

2.1 Линейный конгруэнтный метод 10

2.2 Алгоритм Блюма–Блюма–Шуба 13

3. Разработка программы для проведения экспериментов 18

3.1. Описание разработанной программы 18

3.2. Руководство оператора 25

3.3. Руководство программиста 28

4. Экспериментальное исследование 32

5. Безопасность и экологичность работы 45

ЗАКЛЮЧЕНИЕ 60

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 62

ПРИЛОЖЕНИЕ А 63

1 Теоретические основы криптографического алгоритма Блюма–Блюма–Шуба и линейного конгруэнтного метода

1.1 Линейный конгруэнтный метод

Данный алгоритм был предложен Д. Х. Лемером в 1948 году [1, 2]. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа, задаваемой следующей формулой:

X_n = (aX_n–1 + c) mod M, (1)

где X_n– этоn–ный член последовательности,

X_n–1 – предыдущий член последовательности,

a – множитель,

с– инкремент,

M– модуль.

Обычно используются следующие значения параметров:

• M = 2¹⁶ или 2³² (для простоты реализации);

• a = 1 664 525;

• c = 1 013 904 223.

2 Разработка программы для проведения экспериментов

Разработанная программа содержит в себе 4 основные функции:

а) BBSH() – функция расчета псевдослучайной последовательности алгоритмом Блюма-Блюма-Шуба, представленная в приложении А на странице 31;

1) подпункт 2-го уровня, если нужен;

2) ещё один;

б) LKM() – функция расчета псевдослучайной последовательности линейным конгруэнтным методом, представленная в приложении А на странице 32;

в) ProstChisl() – функция нахождения простых чисел для задания модуля М при помощи решета Эратосфена, представленная в приложении А на странице 25;

г) Graf() – функция вывода графиков по выбранным данным, представленная в приложении А на странице 34.

Блок-схема алгоритма приведена на рисунке 1.

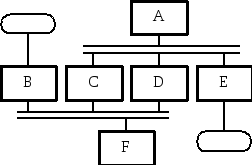
Рисунок 1 – Блок-схема алгоритма

3 Экспериментальное исследование

1. Исследование зависимости времени вычисления от длины генерируемой псевдослучайной последовательности

Это исследование направлено на получение данных о зависимости времени вычисления от длины генерируемой псевдослучайной последовательности. В качестве исходных данных для обоих алгоритмов использовались следующие параметры:

• начальное значение X₀= 57;

• значение максимально возможного модуля М=9967*9967=99341089;

• длина последовательности D изменялась от 10 до 100000, каждый раз увеличивая порядок.

В ходе проведения эксперимента были получены следующие графики, отображенные на рисунках 2 и 3.

Рисунок 2 – Зависимость времени Т от длины последовательности D

Как видно из рисунка 2, при вычислении зависимости времени вычисления от длины генерируемой псевдослучайной последовательности для длины желаемой последовательности порядка 10⁵ оба алгоритма вычисляются примерно равное время. Однако, для длины последовательности порядка 10⁶, как показано на рисунке 3, видно существенное различие по времени подсчета.

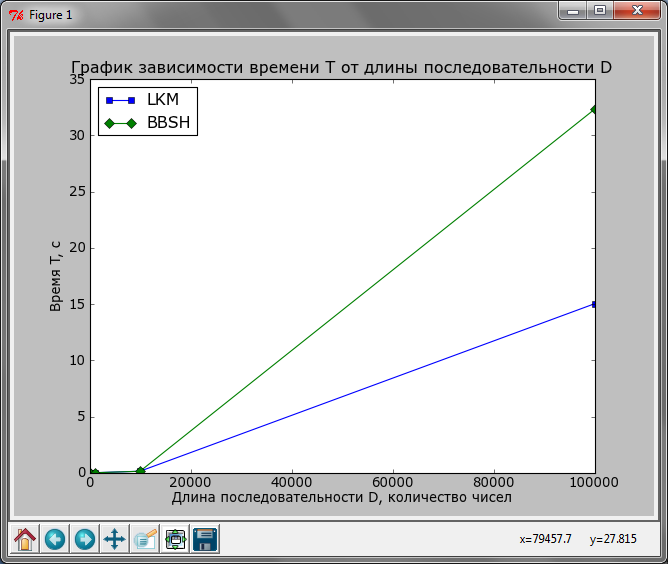
Рисунок 3 – Зависимость времени Т от длины последовательности D

Как показано на рисунке 3, что алгоритм Блюма-Блюма-Шуба работает медленнее, чем линейный конгруэнтный метод практически в 2 раза, что объясняется самим алгоритмом. В линейном конгруэнтном методе используется линейная функция подсчета следующего числа, а в алгоритме Блюма–Блюма–Шуба зависимость между текущим и последующим числом квадратичная, этим и объясняется разница во времени подсчета.