Задание 11
Даны:
векторное поле
и замкнутая
Поверхность , составленная из поверхности второго порядкаи плоскостей. Поверхностьограничена контуром;– нормаль к поверхности, направленная вне замкнутой поверхности.
Найти:
поток
векторного поля
через поверхность
,
в направлении нормали
;
поток
векторного поля
через замкнутую поверхность
в направлении внешней нормали к ее
поверхности, непосредственно и применив
теорему Остроградского;
циркуляцию
векторного поля
по замкнутому контуру
,
непосредственно и применив теорему
Стокса к контуру
и ограниченной им поверхности
с нормалью
.
Сделать чертеж.
Замкнутая поверхность образована поверхностью второго порядка, указанной плоскостью, координатными плоскостями и расположена в первом октанте.
1)
, 
, 
;
2)
, 
, 
;
3)
, 
, 
;
4)
, 
, 
;
5)
, 
, 
;
6)
, 
, 
;
7)
, 
, 
;
8)
, 
, 
;
9)
, 
, 
;
10)
, 
, 
;
11)
, 
, 
;
12)
, 
, 
;
13)
, 
, 
;
14)
, 
, 
;
15)
, 
, 
;
16)
, 
, 
;
17)
, 
, 
;
18)
, 
, 
;
19)
, 
, 
;
20)
, 
, 
;
21)
, 
, 
;
22)
, 
, 
;
23)
, 
, 
;
24)
, 
, 
;
25)
, 
, 
;
26)
, 
, 
;
27)
, 
, 
;
28)
, 
, 
;
29)
, 
, 
;
30)
, 
, 
.
Задание 12
Даны
векторное поле
,
поверхность второго порядка
,
отсеченная плоскостью P.
Найти:
поток
вектора
через внешнюю сторону боковой поверхности
методом
замыкания поверхности
,
применив теорему Гаусса-Остроградского;
циркуляцию
вектора
вдоль контура L,
в положительном направлении полученного
при пересечении поверхности
с плоскостью P,
применив теорему Стокса, и непосредственно.
1)
, 
, 
;
2)
, 
, 
,
3)
, 
, 
;
4)
, 
, 
,
5)
, 
, 
;
6)
, 
, 
,
7)
, 
, 
;
8)
, 
, 
9)
, 
, 
;
10)
, 
, 
,
11)
, 
, 
;
12)
, 
, 
,
13)
, 
, 
;
14)
, 
, 
,
15)
, 
, 
;
16)
, 
, 
,
17)
, 
, 
;
18)
, 
, 
,
19)
, 
, 
;
20)
, 
, 
,
21)
, 
, 
;
22)
, 
, 
;
23)
, 
, 
;
24)
, 
,
,
25)
, 
, 
;
26)
, 
,
у=1,
27)
, 
, 
;
28)
, 
, 
,
29)
, 
, 
;
30)
, 
,
Задание 13
С
помощью теоремы Остроградского-Гаусса
найти поток векторного поля
через полную поверхность тела (V)
в направлении внешней нормали:
1)
, 
2)
, 
3)
,
4)
, 
5)
, 
6)
, 
7)
, 
8)
,
9)
, 
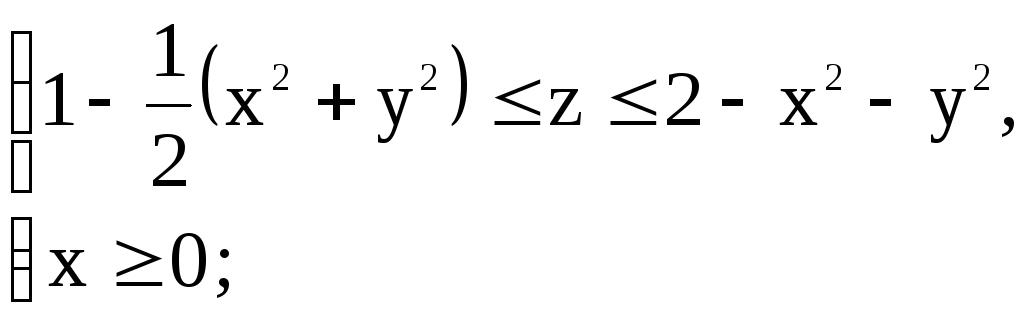
10)
, 
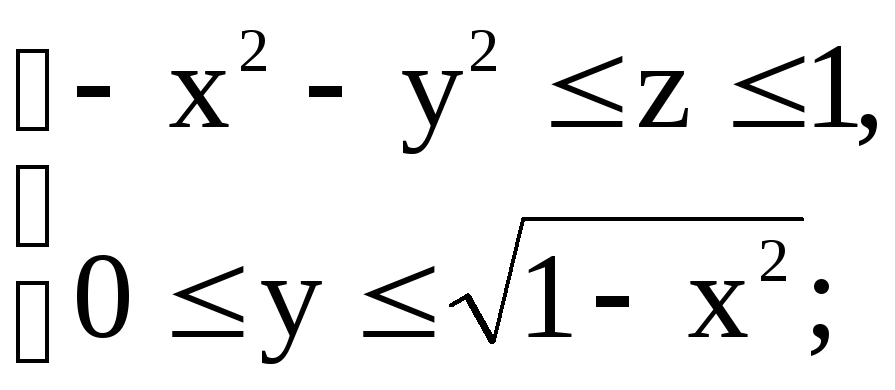
11)
, 
12)
, 
13)
, 
14)
, 
15)
, 
16)
, 
17)
,
18)
, 
19)
, 
20)
, 
21)
, 
22)
, 
23)
, 
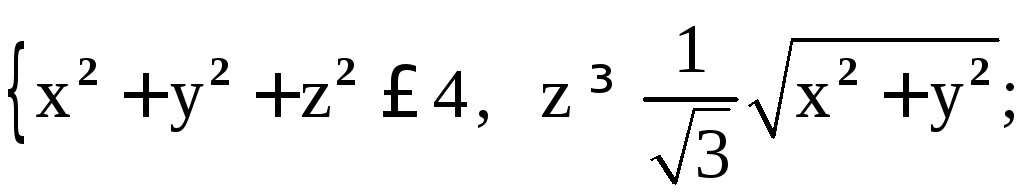
24)
, 
25)
, 
26)
,
27)
,
28)
, 
29)
, 
30)
, 
Задание 14
Доказать,
что поле
потенциально, найти его потенциал и
вычислить работу по перемещению
материальной точки из
в
:
1)
, 
, 
;
2)
, 
, 
;
3)
, 
, 
;
4)
, 
, 
;
5)
, 
, 
;
6)
, 
, 
;
7)
, 
, 
;
8)
, 
, 
;
9)
, 
, 
;
10)
, 
, 
;
11)
, 
, 
;
12)
, 
, 
;
13)
, 
, 
;
14)
, 
, 
;
15)
, 
, 
;
16)
, 
, 
;
17) 
, 
,
;
18)
, 
, 
;
19)
, 
, 
;
20)
, 
, 
;
21) 
, 
,
;
22) 
, 
, 
;
23)
,
;
24)
, 
,
;
25)
, 
, 
26) 
, 
,
;
27)
;
28) 
, 
,
;
29) 
, 
, 
;
30) 
,
,
.
Задание 15
Дано
векторное поле
в цилиндрических координатах. Вычислить
,
.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
22)
;
23)
;
24)
;
25)
;
26)
;
27)
;
28)
;
29)
;
30)
.
Задание 16
Дано
векторное поле
в сферических координатах. Вычислить
.
1)
,
2)
,
3)
,
4)
,
5)
,
6)
,
7)
,
8)
,
9)
,
10)
,
11)
,
12)
,
13)
,
14)
,
15)
,
16)
,
17)
,
18)
,
19)
,
20)
,
21)
,
22)
,
23)
,
24)
,
25)
,
26)
,
27)
,
28)
,
29)
,
30)
.