
Решебник_МО
.pdf
измерения, то можно существенно повысить эффективность поиска. Наиболее эффективным является такое расположение пары измерений, при котором текущий интервал неопределенности сокращается практически вдвое.
МЕТОД ДИХОТОМИИ
Метод дихотомии является самым естественным и наиболее распространенным на практике.
В этом методе оба эксперимента должны быть расположены в районе середины интервала, как можно ближе друг к другу, но так, чтобы можно было отличить значения функции в этих точках друг от друга.
Пусть имеется единичный интервал исследования. Если после
проведения пары экспериментов в оставшемся интервале L2= |
1 |
|
|||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
провести |
|
|
еще |
|
|
пару |
экспериментов, |
то |
получим |
||||||||
L4 |
1 |
|
1 |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Если в L4 провести |
еще |
пару |
|||||||
|
|
|
|
|
|||||||||||||
|
2 |
|
2 |
|
2 |
|
2 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
3 |
|
|
|
1 |
|
7 |
|
|
экспериментов, то можно получить |
L6 |
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
4 |
|
4 |
|
2 |
|
8 |
|
8 |
|
|
Продолжая действовать по этому алгоритму, после k пар экспериментов, получим интервал неопределенности L2k=2-k+(l–2-k)ε.
План проведения эксперимента методом дихотомии приведен на рис. 5.
|
|
1 |
|
|
/2 |
1/2 |
|
0 |
1 |
||
|
(1+ )/2
/2 
 (1+3 )/4 (1+7 )/8
(1+3 )/4 (1+7 )/8
Рис, 5, План проведения поиска методом дихотомии
При использовании метода дихотомии интервал неопределенности Ln после проведения k = n/2 пар экспериментов практически
41
будет равен L0/2n/2. Эффективность метода характеризуется величиной (L0/Ln)дих=2n/2. Уже при n = 10 эффективность метода дихотомии примерно в шесть раз выше метода перебора.
Для сокращения единичного интервала неопределенности до
размера l0 методом дихотомии |
потребуется сделать |
n |
2 |
ln |
1 |
|
||||
ln 2 |
l0 |
|||||||||
|
|
|
|
|
|
|
||||
экспериментов. Для произвольного интервала L0 = [а,в] |
эта формула |
|||||||||
будет иметь вид n |
2 |
ln |
(b a) |
. С ростом n эффективность метода |
||||||
ln 2 |
l0 |
|||||||||
|
|
|
|
|
|
|
|
|||
дихотомии экспоненциально возрастает.
Алгоритм метода дихотомии состоит из следующих шагов.
Ша г 1. Исходный интервал L0 =[a,b] исследования делится пополам.
Ша г 2. Вблизи точки деления (по разные ее стороны) дважды
вычисляется значение целевой функции у(х1), у(х2), где x1= a+L0/2–ε/2; x2=a+L0/2 + ε/2, где ε – наименьший интервал изменения переменной х, при котором возможно обнаружить отличие между y(х1) и у(х2).
Ш а г 3. Используя свойство унимодальных функций, определяют интервал, в котором находится экстремальное значение целевой функции, а затем процесс расчета повторяют по аналогичной схеме до тех пор, пока не будет получен интервал Ln, где Ln 2ε, содержащий точку оптимума х*.
Пример 8. Найти минимум функции f(х) = х4–х3+5х2+х–1 методом дихотомии, отрезок, на котором выполняются замеры, L0= [–2; 2], а минимально допустимый интервал неопределенности, соответствующий минимальному расстоянию между экспери ментами, при котором они различны ε = 0,2 и максимально допустимый интервал неопределенности l0= 0,4.
Решение. Число замеров, необходимых для получения интервала неопределенности заданной точности, можно определить с
помощью формулы |
2 |
ln |
(a b) |
|
2 |
ln |
3,8 |
8,5 . В качестве n |
|
ln 2 |
l0 |
ln 2 |
0,2 |
||||||
|
|
|
|
|
берется ближайшее большее четное число, следовательно, n=10. Согласно оптимальной стратегии поиска первые два замера
42
необходимо выполнить |
в точках |
x 2 |
(2 ( 2)) |
0,1 и |
||||
|
||||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||
x2 |
2 |
(2 ( 2)) |
0,1 . |
Значения |
функции в этих точках будут |
|||
2 |
||||||||
|
|
|
|
|
|
|
||
следующие:
f(x1) = f(–0,1) = х41–х31+5х21+х1–1 = (–0,1)4–(–0,1)3+5٭(–0,1)2+(–0,1)–1≈ ≈ –1,049;
f(x2) = f(0,1) = х41–х32+5х22+х2–1 = (0,1)4–(0,1)3+5*(0,1)2+(0,1)–1≈ –0,851.
Таким образом, в силу унимодальности функции, интервал
неопределенности сократился до L2 = [–2; |
0,1] = 2,1. |
|
|||||||||
|
|
На |
отрезке L2 |
выбираем |
две |
точки |
эксперимента |
||||
x |
|
2 |
(0,1 ( 2)) |
1,05 и |
x 2 |
(0,1 ( 2)) |
0,85 |
вблизи центра |
|||
|
3 |
|
|
2 |
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интервала |
и получаем |
f(x3) = 5,836, |
f(x4) = 2,899. Интервал |
||||||||
неопределенности стал L4 = [–1,05; 0,1]=1,15. |
|
|
|
||||||||
|
|
Далее в близи центра отрезка L4 |
находим точки х5 = –0,575 и |
||||||||
x6 = –0,375, в которых f(x5) = 0,378 и f(x6) = –0,599, а так как f(х5) > f(х6),
то получим интервал L6=[–0,575;0,1] = 0,675. Далее определяем х7 = –0,338 и х8 = –0,138, где f(x7) = –0,715 и f(x8) = –1,04, и так как. f(х7) > f(х8), то интервал неопределенности L8 = [–0,338;0,1] = 0,438. Вновь вблизи центра отрезка неопределенности находим точки
х9 = –0,219 и x10 = –0,019, в которых f(x9) = –0,966 и f(x10) = –1,017.
Интервал неопределенности после пяти пар экспериментов
сократился до L10 = [–0,219;0,1] = 0,319 < 10. Принимаем fmin = f(x10) = = –1,17. Этот минимум достигается в точке х*= x10 = –0,019.
Пример 9. Найдите максимум функции f(х)=3х–2х2–4 методом дихотомии, отрезок, на котором выполняются замеры, L0=[–2,8], минимально допустимый интервал неопределенности, соответствующий минимальному расстоянию между экспериментами, при котором они различны, ε = 0,2, и максимально допустимый интервал неопределенности l0 = 1.
Решение. Число замеров, необходимых для получения интервала неопределенности заданной точности, можно определить с
помощью формулы n |
2 |
ln |
(a b) |
|
2 |
ln |
9,8 |
8. |
|
ln 2 |
l0 |
ln 2 |
0,8 |
||||||
|
|
|
|
|
43

Согласно оптимальной стратегии поиска первые два замера |
|
||||||
необходимо |
выполнить |
в |
точках |
x 2 |
(8 ( 2)) |
2,9 |
и |
|
|||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
x 2 |
(8 ( 2)) |
3,1 . Значения функции в этих точках следующие: |
|
||
2 |
2 |
|
|
|
f(x1) = 3х1–2х21–4 = 3*(2,9)–2*(2,9)2–4 ≈ –12,12; f(x2) = 3х2–2х22–4 = 3*(3,1)–2*(3,1)2–4 ≈ –13,92.
В силу унимодальности функции, интервал неопределенности сократится до L2=[–2; 3,1] = 5,1. В близи центра интервала L2 выбираем две точки для эксперимента х3 = 0,5 и x4 = 0,7, в которых f(x3) = –3,12, f(x4) = –2,88. Интервал неопределенности стал L4 = [0,5;3,1] = 2,6. Проведя третью пару экспериментов получаем: х5 = 1,7 и x6 = 1,9, в которых f(x5) = –4,68 и f(x6) = –5,52, а так как f(х5) > f(х6), то получим интервал L6 = [0,5;1,9] = 0,8.
Вновь вблизи центра отрезка неопределенности L6 находим
точки х7 = 1,1 и х8 = 1,3, где f(x7) = –3,12 и f(x8) = –3,48, и, так как f(х7) >f(х8), интервал неопределенности L8 = [0,5;1,3] = 0,8 < 10. Принимаем
fmax = f(x7) = –3,12. Этот максимум достигается в точке х*= x7 = 1,1. Схема проведения эксперимента приведена на рис. 6.
–
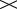
 8
8
– |
|
|
2,9 |
3,1 |
||
0,5 |
|
|
3,1 |
|||
0,7 |
||||||
|
||||||
0,5 |
|
|
3,1 |
|||
|
|
|||||
|
|
|||||
1,7 1,9
0,5 

 1,9
1,9
1,1 1,3
Рис. 6. Схема поиска для примера 9
МЕТОД ФИБОНАЧЧИ
Числами Фибоначчи называют рекуррентную последователь-
ность чисел F0, F1, F2, F3, F4,…, где F0=1, F1=1, Fi=Fi-1+Fi-2, i=2,3,4,…
Сущность метода состоит в том, что эксперименты, проводимые последовательно, располагаются таким образом, чтобы для соседних интервалов неопределенности выполнялось условие Lj=Lj+1+Lj+2. Исключения из этого правила составляют два эксперимента – первый
44

и последний. Так как проведение первого эксперимента не меняет начальный интервал неопределенности, то следует считать L0=L1, а проведение последнего эксперимента фактически соответствует методу дихотомии, поэтому Ln Ln-1/2.
Пусть величина |
|
b a |
|
|
. Тогда b–a=FnΔ, т.е. весь |
|
Fn |
2 |
|||||
|
|
|
|
интервал исследования можно разделить на каждая часть будет иметь длину, меньшую ε ( <ε).
Разобьем отрезок [a,b] на три части с длинами Fn–2* , Fn–3* ,
Fn–3* (это можно сделать, потому что Fn= Fn–1+Fn–2=(Fn–2 + Fn–3)+Fn–2). Точки деления x1 и x2 определяются по формулам (рис. 7):
x1 a Fn 2 , x2 x1 Fn 3 a Fn 1 .
Рис. 7. Положение первых двух точек метода Фибоначчи
В найденных точках вычисляются значения целевой функции f(х1), f(х2) и среди них выбирается большее при поиске максимума (соответственно меньшее – при поиске минимума). Если искомое экстремальное значение достигнуто в точке xi, то в качестве следующего интервала неопределенности выбирается интервал [a,xi], в противном случае [xi-1,b]. В полученном интервале находится точка замера, где значение функции было экстремальным. Для продолжения поиска необходимо точку следующего замера расположить симметрично этому имеющемуся замеру, а далее поиск осуществляется аналогично рассмотренному. На последнем шаге длина интервала будет равна F3* =3*Δ, а точки деления разделят его на три отрезка длиной F1* =F0* = . Таким образом, точка искомого экстремума определяется с точностью 2Δ≤ε.
Из сказанного нетрудно установить, что для любого (n–k)-го эксперимента справедлива формула Ln-k=Fk+1Ln, где через Fk – числа Фибоначчи.
Эффективность метода Фибоначчи характеризуется величиной (L0/Ln)фиб=(L1/Ln)фиб=Fn и при n=10 превышает метод дихотомии более,
45

чем в 2,5 раза. С ростом n преимущество метода еще больше возрастает. Недостаток метода состоит в том, что им нельзя пользоваться, не зная заранее общего числа экспериментов n. Если поиск методом Фибоначчи начат, то на любом шаге действия определяются просто: каждый последующий эксперимент располагается симметрично относительно предыдущего, попавшего в этот же интервал неопределенности. Однако для определения места приложения первых двух экспериментов необходимо найти величину Ln, которая определяется по формуле L2=L1(Fn-1/Fn) и зависит от числа экспериментов n.
Алгоритм метода Фибоначчи следующий.
Ш а г 1. По заданной точности ε рассчитывается
вспомогательное число N b a . l0
Ш а г 2. Для полученного значения N находится такое число Фибоначчи Fn, чтобы выполнялось неравенство Fn-1<N Fn.
Ш а г 3. Определяется минимальный шаг поиска по формуле
m b a . Fn
Ша г 4. Рассчитывается значение функции f(x) в начале интервала, т.е. f(a).
Ша г 5. Следующая точка, в которой вычисляется значение
f(x): х1=аn+mFn–2.
Ша г 6. Если f(x1)>f(a) (шаг удачный при поиске max f(x)), то следующая точка определяется как x2 = x1+mFn–3; при f(x1) ≤ f(a) (шаг неудачный при поиске max f(x)) определим х2 = х1–mFn–3.
Ша г 7. Последующие шаги выполняются с уменьшающейся величиной шага в соответствии со следующим правилом. Если при
выполнении шага значение функции в точке xi+1 = xi+ xi оказывается больше, т.е. f(xi+1) > f(xi) – шаг удачный, то следующий (i+2)-й шаг выполняется из точки хi+1: xi+2 = xi+1+ xi+1. Если (i+1)-й шаг неудачный, т.е. f(xi+1) ≤ f(xi), то следующий (i+2)-й шаг выполняется из точки хk – точки последнего лучшего результата в обратном направлении, т.е. xi+2 = xk–Δxi+1. Для каждого i-го шага Δxi вычисляется
по формуле x |
mF |
. |
i |
n i 2 |
|
46
Указанный процесс продолжим до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности. Точка последнего измерения берется посередине отрезка Ln–1.
Пример 10. Найдите положение минимум функции f(х)=х4–х3+5х2+х–1 методом Фибоначчи. Отрезок, на котором исследуется функция L0=[–2; 2], максимально допустимый интервал неопределенности l0 = 0,2, минимально допустимый интервал, соответствующий минимальному расстоянию между экспериментами, при котором они различны ε = 0,1.
|
Решение. В соответствии с алгоритмом найдем N= |
b a |
= |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
l0 |
|
||
= |
2 ( 2) |
=20. Имеем F6<N=20<F7, откуда Fn=F7=21 и n=7. |
|
|
|
|
|||
0,2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Определим максимальный шаг поиска: m |
2 ( 2) |
|
4 |
|
0,19 . |
|||
|
|
|
|
|
|||||
|
|
|
F7 |
21 |
|
||||
Вычислим в начале интервала (в точке а = –2) значение исследуемой функции: f(a) = f(–2) = 41.
Найдем точку х1: x1 = a+mFn–2 = a+mF5 = –2+0,19*8 = –0,476, в
которой вычислим значение f1:
f(x1) = (–0,476)4–(–0,476)3+5*(–0,476)2+(–0,476)–146–29,6 = –0,183.
Так как f(x1) < f(a) (это удачный шаг при поиске минимум функции), то следующая точка х2 определяется по формуле
x2 = x1+mFn–3 = х1+mF4 = –0,476+0,19*5 = 0,386. Значение функции f(х2) = 0,553, а L2 = [–2; –0,386] = 2,386.
Так как f(x2) > f(x1) (шаг неудачный), то, в соответствии с алгоритмом, следующий шаг выполняется из точки х1 в противоположную сторону, т.е.
xi+1 = х3 = x1–mFn–i–2= x1–mF3= –0,476–0,19*3 = –1,048 и f3 = 5,794. Из результатов вычисления следует, что L3 = [–1,048 ;0,386] = 1,134.
Так как f3 > f1 (шаг неудачный), то направление шага (т.е. знак приращения) вновь меняется, и следующий шаг выполняется из точки х1: х4 = х1+mF2 = –0,476+0,19*2 = –0,095, f4 = –1,049. Из условия f3 > f4 следует, что L4 = [–0,476; 0,386] = 0,862.
Так как f4<f1 (шаг удачный), то направление шага не меняется:
47

х5 = х4+mF1 = –0,095+0,19*l = 0,095, f5 = –0,86. Из условия f5 > f4 следует, что L5 = [–0,476; 0,095] = 0,571.
Так как f5>f4 (шаг неудачный), то меняем направление шага:
х6 = х4–mF0 = –0,095–0,19*l = –0,285, f5 = –0,848. Из условия f6 > f4 следует, что L6 = [–0,285; 0,095] = 0,38.
Точка последнего измерения x7 находится путем деления отрезка L6 пополам: x7 = –0,095, т.е. мы вернулись в точку х4, значение функции в которой уже вычислялось, а L7 = [–0,095; 0,095] = 0,19 < l0.
За семь измерений лучший результат получен в точке х4 = х7, следовательно решением является точка: х*= –0,095 и f(x*) = –1,049.
Пример 11. Найдите максимум функции f(х) = 3х+2х2–4 методом Фибоначчи, отрезок, на котором выполняются замеры, L0=[–2; 8], минимально допустимый интервал неопределенности, соответ-ствующий минимальному расстоянию между экспериментами, при котором они различны, ε = 0,4, и максимально допустимый интервал неопределенности l0 = 0,8.
Решение. В соответствии с алгоритмом найдем N= b a = l0
= |
8 ( 2) |
=10. Имеем F5 < N = 10 <F6, откуда Fn= F6 = 13 и n = 6. |
|||||||
0,8 |
|||||||||
|
|
|
|
|
|
|
|
||
Определим максимальный шаг поиска: |
m |
b a |
|
10 |
0,77 . |
||||
|
|
|
|||||||
|
|
|
|
Fn |
13 |
|
|||
Вычислим значение исследуемой функции в начале и конце интервала
(в точках а = –2, в = 8): f(–2) = –18, f(8) = –108. В силу того, что определяется максимум функции, поиск целесообразно начинать в начальной точке интервала исследования и двигаться к его концу.
Найдем точку х1: x1 = а+mFn–2 = в–mF4 = –2+0,77*5 = 1,85, в
которой вычислим значение: f(x1) = –5,295.
Так как f(x1) > f(а) (шаг удачный), то следующая точка х2
определяется по формуле: x2 = x1+mFn–3 = х1+mF3 = 1,85+0,77*3 = 4,16
и f(x2) = –26,13. Поскольку f2 < f1, то, учитывая унимодальность функции, получим L2 = [–2; 4,16] = 6,16.
Так как f2 < f1 (шаг неудачный), то направление шага (т.е. знак приращения) меняется, и следующий шаг выполняется из точки х1:
48

х3 = х1–mF2 = 1,85–0,77*2 = 0,31, f3 = –3,26. Из условия f3 > f1 следует, что L3 = [–2; 1,85] = 3,85.
Так как f3>f1 (шаг удачный), то направление следующего шага не меняется: х4 = х3–mF1 = 0,31–0,77*l = –0,46, f4 = –5,8. Из условия f4 < f3 следует, что L4 = [–0,46; 1,85] = 2,31.
Так как f4<f3 (шаг неудачный), то направление шага (т.е. знак приращения) меняется, и следующий шаг выполняется из точки х3:
х5 = х3+mF0 = 0,31+0,77*1 = 1,01, f5 = –3,01. Из условия f5>f3 следует, что L5 = [0,31; 1,85] = 1,54.
Точка последнего измерения x6 находится путем деления отрезка L5 пополам: x6 = 1,08, , f6 = –3,09. Из условия f6 < f5 следует,
что L6 = [0,31; 1,01] = 0,7 < l0.
За шесть измерений лучший результат получен в точке х5, следовательно решением является точка: х*= х5 = 1,01 и f(x*) = –3,01.
МЕТОД ЗОЛОТОГО СЕЧЕНИЯ
Метод Фибоначчи требует предварительного знания необходимого числа опытов. Однако задача поиска может быть поставлена таким образом, что необходимо найти не собственно максимум, а то значение аргумента, при котором выполняется некоторое условие, например f(x) Y. В этом случае оценить заранее требуемое число измерений не представляется возможным. Значит, нельзя определить и положение первого эксперимента для поиска по методу Фибоначчи.
Избежать зависимости первого опыта от числа опытов позволяет метод золотого сечения. Метод золотого сечения (ЗC), как и метод Фибоначчи, требует выполнения условия Lj=Lj+1+Lj+2. Однако в отличие от последнего он предполагает постоянство отношений длин последовательных интервалов неопределенности: Lj/Lj+1=Lj+1/Lj+2=C,
где C (1 
 5) / 2 1,618.
5) / 2 1,618.
Поиск по методу ЗС производится так же, как и по методу Фибоначчи. Отличие заключается лишь в проведении первых двух
экспериментов. Первое измерение делается на расстоянии L1 |
L0 |
от |
|
||
|
C |
|
любого края исходного интервала неопределенности, где L0=b–a. Второе измерение делается симметрично первому. Поэтому
49
координаты |
|
первых |
двух замеров определяются по |
формулам: |
||||
x a |
b a |
, |
x |
|
b |
b a |
. |
|
1 |
c |
|
2 |
|
c |
|
|
|
|
|
|
|
|
|
|||
|
Два |
|
замера |
позволяют сократить исходный |
интервал |
|||
неопределенностей до величины L2=x2–а, если искомое экстремальное значение функции достигается в точке x1, или до величины L2=b–x1, если экстремальное значение достигается в точке x2. В полученном интервале уже имеется один замер, а следующий замер располагается симметрично ему.
Замеры выполняются до тех пор, пока величина интервала, содержащая искомый экстремум, не сократится до величины Ln≤ ε или будет достигнута заданная точность решения.
Нетрудно видеть, что после проведения n экспериментов интервал неопределенности метода станет Ln=L0/Cn-1. Эффективность
метода характеризуется величиной (L0/Ln)зол=Cn-1. |
|
||||||||
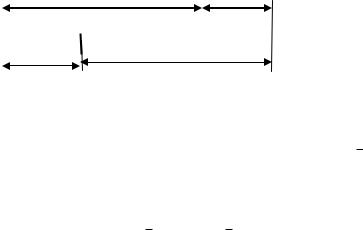
На рис. 8 |
приведено взаимное расположение первых |
двух |
|||||||
|
|
|
1/с |
|
|
1/с2 |
|
||
|
|
|
х2 |
х1 |
|
|
|
||
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
1/с |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1/с |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис, 8, Расположение первых двух точек по методу ЗС |
|
||||||||
измерений по методу золотого сечения. |
|
||||||||
Математик |
Люкас вывел |
уравнение, связывающее |
числа |
||||||
Фибоначчи Fn и величину С: при больших n получается Fn Cn+1/ 
 5 . Это соотношение дает возможность получить связь величины интервалов неопределенности Ln после n опытов проведенных по методу золотого сечения и по методу Фибоначчи:
5 . Это соотношение дает возможность получить связь величины интервалов неопределенности Ln после n опытов проведенных по методу золотого сечения и по методу Фибоначчи:
(Ln)зол/(Ln) Сn+1/( 
 5 Cn–1)=C2/
5 Cn–1)=C2/ 
 5 =1,17.
5 =1,17.
Пример 12. Найдите значение аргумента, при котором значение функции f(х) = х4–х3+5х2+х–1, заданной на интервале L0 = [–2; 2], будет меньше (–1).
Решение. Применяя метод «золотого сечения», получим
50
