12. Как определяются интервал неопределенности Ln метода золотого сечения?

После нахождения x1 (x1=длина_интервала/1.62) и x2 (x2=длина_интервала-x1) и значений функции y1 = f(x1) и y2 = f(x2) необходимо сравнить их с условием, принимая во внимание свойство унимодальности. Если подходит x1, то интервал берется [x2; конец], если берем x2, то следующим интервалом будет [x1; конец].

13.Как определить положение первых двух измерений при поиске экстремума функции методом Фибоначчи?

14. Как определяются интервал неопределенности метода Фибоначчи?

15. Как связаны между собой интервалы неопределенности Ln метода Фибоначчи и золотого сечения?

16. Как оценивается эффективность одномерного поиска.

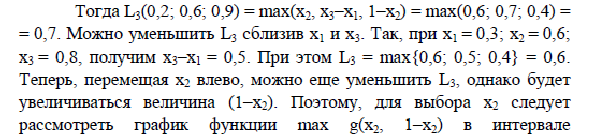
дихотомия

Эффективность метода охарактеризуется величиной: (L0/Ln) = 2^-n\2 . n-количество экспериментов. L-интервал

Последовательный поиск

Эффективность процесса поиска можно оценить отношением (L0/Ln)=(n+1)/2.

Эффективность метода Фибоначчи наивысшая из рассматриваемых методов. Она характеризуется величиной (L0/Ln)фиб=(L1/Ln)фиб=Fn и при n=10 превышает метод дихотомии более, чем в 2,5 раза.

Золотого сечения

Эффективность метода характеризуется величиной (L0/Ln)зол=C^n-1.

Альтернативная версия ответа на тот же вопрос:

Как оценивается эффективность одномерного поиска.

Большое разнообразие итерационных алгоритмов ставит перед пользователем задачу выбора. Для этого следует выставить критерии, на основании которых один алгоритм будет считаться более предпочтительным, нежели другой. С этой целью обычно используют следующие оценки:

1. Точность поиска – значение окрестности локального оптимума, в которую приводит алгоритм после выполнения заданного числа итераций.

2. Скорость сходимости – число итераций, необходимое для достижения заданной точности.

3. Время счета – время поиска на ЭВМ локального оптимума с заданной точностью, отнесенное к коэффициенту сложности задачи (или к быстродействию ЭВМ).

4. Стабильность – свойство алгоритма незначительно увеличивать число итераций при малых возмущениях выбора начальных точек, а также вследствие погрешности вычислений.

5. Надежность - свойство алгоритма приводить к оптимуму при многократном повторении поиска из разных начальных точек.

Для сравнения алгоритмов по этим критериям следует производить расчеты в одинаковых или близких условиях.

17. Как определяется положение новой точки Хк+1 при поиске оптимума функции методом релаксации?

Метод релаксации Этот метод имеет наиболее простую процедуру поиска. Его алгоритм заключается в отыскании осевого направления, вдоль которого функция цели изменяется наиболее сильно. Для этого в начальной точке поиска определяются производные оптимизируемой функции f(X) по всем переменным. Затем выбирается наибольшая по модулю производная, и соответствующая ей переменная изменяется до достижения частного оптимума. В новой точке определяются производные по всем остальным переменным, и осуществляется поиск следующего частного оптимума и т.д.

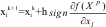
где Xр - точка, в которой последний раз определялись производные;

хi, - координата с наибольшей по модулю производной в точке Хр ;

signZ-> возвращает знакZили 0 еслиZ== 0

18. Как определяется положение новой точки Хк+1 при поиске оптимума функции равномерным градиентным методом?

Основная проблема в градиентных методах – это выбор шага k. Достаточно малый шагk обеспечивает убывание функции, то есть выполнение неравенства:

но может привести к неприемлемо большому количеству итераций, необходимых для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции (невыполнение условия убывания) либо привести к колебаниям около точки минимума. Однако проверка условия убывания на каждой итерации является довольно трудоемкой, поэтому в методе градиентного спуска с постоянным шагом задают =k постоянным и достаточно малым, чтобы можно было использовать этот шаг на любой итерации. При этом приходится мириться с возможно большим количеством итераций. тешением является лишь то, что трудоемкость каждой итерации, в этом случае, минимальна (нужно вычислять только градиент f’(xk)).

Формула для нахождения Хк+1:

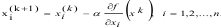
Где а – размер шага итерации.

19. Как определяется положение новой точки Хк+1 при поиске оптимума функции пропорциональным градиентным методом?

20. Как определяется положение новой точки Хк+1 при поиске оптимума функции методом наискорейшего спуска (подъема)?