
- •Методы оптимизации. Ответы на вопросы.
- •Конечномерные экстремальные задачи без ограничений.
- •Конечномерные экстремальные задачи с ограничениями.
- •Свойства выпуклых множеств.
- •Выпуклые оболочки.
- •Проекция точки на множество.
- •Отделимость выпуклых множеств.
- •Свойства выпуклых функций.
- •Критерии выпуклости функций.
- •Минимум выпуклой функции.
- •Функция Лагранжа и седловая точка.
- •Теорема Куна-Таккера.
- •Связь между основной и двойственной задачами.
- •Условия сходимости градиентных методов.
- •Условия сходимости метода Ньютона.
- •Условие сходимости метода штрафных функций.
- •Условие сходимости методов возможных направлений
- •Вариация функционала
- •Доказательство.
- •Простейшая задача вариационного исчисления.
- •Доказательство.
- •Уравнение Эйлера-Лагранжа
- •Условия Лежандра и Якоби
- •Доказательство.
- •Постановка вариационной задачи с подвижными границами.
- •Доказательство:
- •Задача Больца
- •Изопериметрическая задача.
- •Задача Лагранжа
- •Метод Ритца
- •Общая постановка задачи оптимального управления.
- •Достаточное условие существования решения задачи оптимального управления.
- •Принцип максимума л. С. Понтрягина. Необходимые условия.
- •Принцип Эйлера-Лагранжа и оптимальное управление
- •Необходимые условия в задаче теории оптимального управления
- •Принцип максимума Понтрягина для простейшей задачи оптимального управления
- •Задача линейного быстродействия.
- •Достаточные условия оптимальности в задаче линейного быстродействия.
- •Фундаментальная матрица и формула Коши.
- •Принцип Крейна.
-
Условия сходимости метода Ньютона.
Перейдем
к изложению метода второго порядка,
использующего вторые частные производные
минимизируемой функции
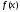 .
Этот метод является прямым обобщением
метода Ньютона для отыскания решения
систем уравнений
.
Этот метод является прямым обобщением
метода Ньютона для отыскания решения
систем уравнений
 ,
где
,
где
 .
Возьмем линейную аппроксимацию функции
.
Возьмем линейную аппроксимацию функции
 в окрестности точки
в окрестности точки
 и перепишем уравнение в следующем виде:
и перепишем уравнение в следующем виде:

Отбрасывая
последний член в этом разложении, получим
линейную систему уравнений относительно
нового приближения
 .
Таким образом, метод Ньютона отыскания
решения системы уравнений описывается
следующей формулой:
.
Таким образом, метод Ньютона отыскания
решения системы уравнений описывается
следующей формулой:

Рассмотрим
теперь случай, когда
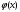 является градиентом некоторой функции
является градиентом некоторой функции
 .
Формула метода Ньютона для решения
уравнения
.
Формула метода Ньютона для решения
уравнения
 выглядит
так:
выглядит
так:

В
этом случае метод Ньютона может
интерпритировать как поиск точки
минимума квадратичной аппроксимации
функции
 в окрестности точки
в окрестности точки
 .
.
Лемма1.
Пусть
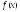 дважды непрерывно дифференцируемая
функция. Если
дважды непрерывно дифференцируемая
функция. Если
 -сильно
выпуклая функция с константой
-сильно
выпуклая функция с константой
 ,
то выполняется следующее неравенство:
,
то выполняется следующее неравенство:
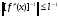
Доказательство.
Пользуясь
Теоремой о среднем, получим следующие
формулы для конечных приращений функции
 :
:
 ,
где
,
где
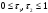
Воспользуемся
условием сильной выпуклости

Заменяя
 на
на
 ,
получим:
,
получим:
 .Следовательно,
.Следовательно,
 .
.
Поделив
на
 и устремив
и устремив
 к нулю, будем иметь
к нулю, будем иметь
 .
.
Положим
 и, используя неравенство Коши-Буняковского,
получим
и, используя неравенство Коши-Буняковского,
получим
 для любого
для любого
 .
Это означает, что
.
Это означает, что
 .
Лемма доказана.
.
Лемма доказана.
Пусть
последовательность
 получена
с помощью метода Ньютона и точка
получена
с помощью метода Ньютона и точка
 - глобальный минимум функции
- глобальный минимум функции
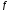 .
Нижеследующая теорема устанавливает
условия квадратичной скорости сходимости
метода.
.
Нижеследующая теорема устанавливает
условия квадратичной скорости сходимости
метода.
Теорема
1.
Пусть дважды непрерывно дифференцируемая
функция
 сильно выпукла (с константой
сильно выпукла (с константой
 ),
а вторая производная удовлетворяет
условию Липшица
),
а вторая производная удовлетворяет
условию Липшица
 ,
для любых
,
для любых
 ,
и
,
и
 .
Тогда
.
Тогда
 и метод Ньютона имеет квадратичную
скорость сходимости
и метод Ньютона имеет квадратичную
скорость сходимости
 .
.
Доказательство.
Воспользуемся
следующей формулой конечных приращений:
 .
Подставим вместо
.
Подставим вместо
 производную функции
производную функции
 и, применяя неравенство Коши-Буняковского,
получим
и, применяя неравенство Коши-Буняковского,
получим
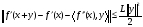 .
Тогда для
.
Тогда для
 и
и
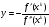 имеем
имеем
 .
Применяя лемму 1, получим
.
Применяя лемму 1, получим
 .
Итерируя это неравенство по
.
Итерируя это неравенство по
 ,
приходим к неравенству
,
приходим к неравенству
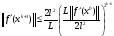 ,
,
 .
Остается показать, что
.
Остается показать, что
 .
Из определения 1 (п.6.3) сильной выпуклости
имеем
.
Из определения 1 (п.6.3) сильной выпуклости
имеем
 .
Тогда при подстановке
.
Тогда при подстановке
 ,
учитывая равенство
,
учитывая равенство
 ,
получим
,
получим
 ,
откуда и следует требуемое неравенство.
,
откуда и следует требуемое неравенство.
-
Условие сходимости метода штрафных функций.
Метод штрафных функций применяется для решения задач условной оптимизации и относится к методам последовательной безусловной минимизации. Основная идея метода заключается в сведении исходной задачи:
 (1)
(1)
 (2)
к последовательности задач оптимизации
(2)
к последовательности задач оптимизации
 (3),
где
(3),
где
 некоторая
вспомогательная функция, которая
подбирается так, чтобы с ростом номера
некоторая
вспомогательная функция, которая
подбирается так, чтобы с ростом номера
 она
мало отличалась от исходной функции
она
мало отличалась от исходной функции
 на
множестве
на
множестве
 и
быстро возрастала на множестве
и
быстро возрастала на множестве
 .
Быстрый рост
.
Быстрый рост
 вне
вне
 приводит
к тому , что при больших
приводит
к тому , что при больших
 нижняя
грань этой функции на
нижняя
грань этой функции на
 будет
достигаться в точках, близких к множеству
будет
достигаться в точках, близких к множеству
 ,
и решения задачи (3) будет приближаться
при определенных условиях к решению
исходной задачи (1)-(2). При этом имеется
достаточно большой произвол в выборе
функций
,
и решения задачи (3) будет приближаться
при определенных условиях к решению
исходной задачи (1)-(2). При этом имеется
достаточно большой произвол в выборе
функций
 .
Это позволяет подобрать наиболее удобный
вид минимизируемой функции
.
Это позволяет подобрать наиболее удобный
вид минимизируемой функции
 и
применять более простые методы безусловной
оптимизации.
и
применять более простые методы безусловной
оптимизации.
Опр.
1
Функция
 называется
штрафной
функцией
множества
называется
штрафной
функцией
множества
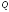 ,
если
,
если
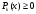 для
любых
для
любых
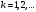 ,
,
 и
и

Из
этого определения видно, что при больших
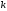 за
нарушение условия
за
нарушение условия
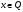 приходится платить большой штраф, в то
время как при
приходится платить большой штраф, в то
время как при
 этот штраф стремится к нулю с ростом
этот штраф стремится к нулю с ростом
 (рис.1).
(рис.1).

Рис.1 Штрафные функции
Для
любого множества Q
можно
указать сколь угодно много штрафных
функций. Пусть
 и
и
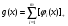 .Теперь
множество допустимых решений представимо
в виде:
.Теперь
множество допустимых решений представимо
в виде:
 , и штрафными функциями являются,
например, следующие:
, и штрафными функциями являются,
например, следующие:

Пусть
штрафная функция
 уже выбрана. Положим
уже выбрана. Положим
 и будем считать, что
и будем считать, что
 ,
для всех
,
для всех
 .
(4)
.
(4)
Тогда,
для каждого k
можно постараться найти решение задачи
(3) и получить последовательность
оптимальных решений. К сожалению, нижняя
грань в (4) может достигаться не при всех
k.
Поэтому зададимся последовательностью
 такой, что
такой, что
 и
и
 при
при
 и
с помощью какого-либо метода безусловной
оптимизации найдем точки
и
с помощью какого-либо метода безусловной
оптимизации найдем точки
 ,
удовлетворяющие условию
,
удовлетворяющие условию
 .
(5)
.
(5)
Другими
словами, вместо точного решения
 будем искать приближенное решение
будем искать приближенное решение
 с погрешностью, не превышающей
с погрешностью, не превышающей
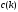 .
Отметим, что, вообще говоря,
.
Отметим, что, вообще говоря,
 может не принадлежать Q.
Дальнейшее изложение уже не зависит от
того, каким именно методом найдена точка
может не принадлежать Q.
Дальнейшее изложение уже не зависит от
того, каким именно методом найдена точка
 .
Поэтому ограничимся предположением о
существовании такого метода и перейдем
к исследованию сходимости метода
штрафных функций.
.
Поэтому ограничимся предположением о
существовании такого метода и перейдем
к исследованию сходимости метода
штрафных функций.
Пусть
штрафные функции
 задаются с помощью вспомогательных
функций
задаются с помощью вспомогательных
функций
 равенствами
равенствами
 и
и
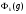 такова, что
такова, что
а)
 определены
и непрерывны для всех
определены
и непрерывны для всех
 ;
;
б)
 положительны, монотонно возрастают по
положительны, монотонно возрастают по
 и
и
 для
для
 ;
;
с)
 сходится
к 0 равномерно при
сходится
к 0 равномерно при
 в области
в области
 .
Тогда следующая теорема дает достаточные
условия сходимости метода штрафных
функций.
.
Тогда следующая теорема дает достаточные
условия сходимости метода штрафных
функций.
Теорема
1.
Пусть функция f,
g
определены
и непрерывны на
 ,
,
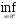
 ,
штрафные функции удовлетворяют условиям
a),
b),
c)
и последовательность
,
штрафные функции удовлетворяют условиям
a),
b),
c)
и последовательность
 определяется соотношениями (5) (п.8.1).
Тогда
определяется соотношениями (5) (п.8.1).
Тогда
1)

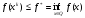 и
и
 ;
2) если
;
2) если
 принадлежит
множеству L
принадлежит
множеству L предельных точек последовательности
предельных точек последовательности
 ,
то
,
то
 и
и
 ;
3) если множество
;
3) если множество
 ограничено
для некоторого
ограничено
для некоторого
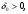 то
то
 и
и при
при
 .
.
Доказательство.
1)
По определению
 существует
последовательность
существует
последовательность
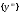 ,
,
 ,
для которой
,
для которой
 при
при
 .
Тогда для любого
.
Тогда для любого
 найдутся
номера
найдутся
номера
 ,
,
 ,
такие, что
,
такие, что
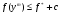 ,
,
 при
при
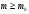 ,
,
 .
Учитывая
.
Учитывая
 и
условие с), можно считать, что
и
условие с), можно считать, что
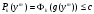 при
при
 ,
,
 .
Из этих неравенств и условий теоремы
имеем
.
Из этих неравенств и условий теоремы
имеем
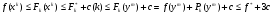 .
.
Следовательно,
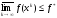 .
Заметим, что при
.
Заметим, что при
 справедливо неравенство
справедливо неравенство
 .Покажем,
что отсюда следует неравенство
.Покажем,
что отсюда следует неравенство
 Предположим,
что верно обратное неравенство. Тогда
существует последовательность
Предположим,
что верно обратное неравенство. Тогда
существует последовательность
 ,
для которой
,
для которой
 для
всех s
больших некоторого
для
всех s
больших некоторого
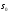 .
Из условия b)
имеем
.
Из условия b)
имеем
 при
при
 .
Противоречие.
.
Противоречие.
2)
Пусть
 .
Тогда существует последовательность
.
Тогда существует последовательность
 сходящаяся
к
сходящаяся
к
 .
Функция
.
Функция
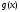 непрерывна
и, как доказано раннее,
непрерывна
и, как доказано раннее,
 .
Поэтому
.
Поэтому
 .
.
Следовательно,
 .
Из условий теоремы имеем
.
Из условий теоремы имеем
 ,
а из определения верхнего предела
следует обратное неравенство
,
а из определения верхнего предела
следует обратное неравенство
 .
Поэтому
.
Поэтому
 .
.
3)
Докажем, что из установленного неравенства

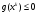 следует
следует
 при
при
 .
Предположим, что существует
.
Предположим, что существует
 такое, что для любого
такое, что для любого
 найдется номер
найдется номер
 ,
для которого
,
для которого
 .
Рассмотрим подпоследовательность
.
Рассмотрим подпоследовательность
 .
Из условия
.
Из условия
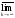
 следует, что существует номер
следует, что существует номер
 такой, что для любого
такой, что для любого
 справедливо
справедливо
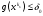 .
Так как множество
.
Так как множество
 компактно, то без ограничения общности
можно считать, что подпоследовательность
компактно, то без ограничения общности
можно считать, что подпоследовательность
 сходится к точке
сходится к точке
 .
Из непрерывности функции
.
Из непрерывности функции
 получим
получим
 и следовательно,
и следовательно,
 .
Учитывая компактность множества
.
Учитывая компактность множества
 ,
с помощью неравенства треугольника
легко доказать, что для любых точек
,
с помощью неравенства треугольника
легко доказать, что для любых точек
 справедливо неравенство
справедливо неравенство
 .Следовательно,
функция
.Следовательно,
функция
 непрерывна. Тогда
непрерывна. Тогда
 .Поэтому
справедливо неравенство
.Поэтому
справедливо неравенство
 .
В то же время выше доказано, что
.
В то же время выше доказано, что
 .
Получаем противоречие. Показано, что
из неравенства
.
Получаем противоречие. Показано, что
из неравенства

 следует
следует
 при
при
 .
Аналогичным образом можно показать,
что из неравенства
.
Аналогичным образом можно показать,
что из неравенства

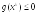 следует
следует
 .
ч.т.д.
.
ч.т.д.
Заметим, что метод штрафных функций в некотором смысле близок к методу множителей Лагранжа. В самом деле, при составлении функции Лагранжа ограничения задачи заносятся в целевую функцию с неизвестными множителями, что можно рассматривать как штраф за нарушение соответствующих ограничений. Достоинством метода множителей Лагранжа является то, что в нем отсутствуют неограниченно растущие коэффициенты типа штрафных коэффициентов. В то же время метод множителей Лагранжа предполагает существование седловой точки, а метод штрафных функций может использоваться для более широких классов задач и является более универсальным.
