
- •Методы оптимизации. Ответы на вопросы.
- •Конечномерные экстремальные задачи без ограничений.
- •Конечномерные экстремальные задачи с ограничениями.
- •Свойства выпуклых множеств.
- •Выпуклые оболочки.
- •Проекция точки на множество.
- •Отделимость выпуклых множеств.
- •Свойства выпуклых функций.
- •Критерии выпуклости функций.
- •Минимум выпуклой функции.
- •Функция Лагранжа и седловая точка.
- •Теорема Куна-Таккера.
- •Связь между основной и двойственной задачами.
- •Условия сходимости градиентных методов.
- •Условия сходимости метода Ньютона.
- •Условие сходимости метода штрафных функций.
- •Условие сходимости методов возможных направлений
- •Вариация функционала
- •Доказательство.
- •Простейшая задача вариационного исчисления.
- •Доказательство.
- •Уравнение Эйлера-Лагранжа
- •Условия Лежандра и Якоби
- •Доказательство.
- •Постановка вариационной задачи с подвижными границами.
- •Доказательство:
- •Задача Больца
- •Изопериметрическая задача.
- •Задача Лагранжа
- •Метод Ритца
- •Общая постановка задачи оптимального управления.
- •Достаточное условие существования решения задачи оптимального управления.
- •Принцип максимума л. С. Понтрягина. Необходимые условия.
- •Принцип Эйлера-Лагранжа и оптимальное управление
- •Необходимые условия в задаче теории оптимального управления
- •Принцип максимума Понтрягина для простейшей задачи оптимального управления
- •Задача линейного быстродействия.
- •Достаточные условия оптимальности в задаче линейного быстродействия.
- •Фундаментальная матрица и формула Коши.
- •Принцип Крейна.
-
Отделимость выпуклых множеств.
Опр.
1:
Множества
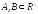 отделимы, если существует вектор
отделимы, если существует вектор
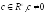 ,
что
,
что
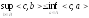 (1) строго отделимы, если
(1) строго отделимы, если
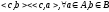 и сильно отделимы, если в (1) знак
неравенства строгий.
и сильно отделимы, если в (1) знак
неравенства строгий.
Замечание: Геометрический смысл О.1 в существовании гиперплоскости, что А и В лежат в разных полупространствах по отношению к ней. Гиперплоскость отделяющая (строго, сильно).
Теорема
1:
Пусть
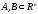 непустые, выпуклые и
непустые, выпуклые и
 =
=
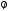 .
Тогда существует гиперплоскость
.
Тогда существует гиперплоскость
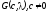 ,
отделяющая
,
отделяющая
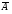 и
и
 .
Если
.
Если
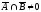 и
и
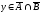 ,
то
,
то

Доказательство:
Пусть
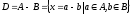 .
.
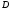 выпукло (Т.2, П.2.1).
выпукло (Т.2, П.2.1).
 .
.
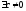 ,
что
,
что
 (Т.3, П.2.3). Тогда
(Т.3, П.2.3). Тогда
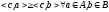 (2)
(2)
Пусть
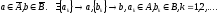 .
.
Из
(2)
 ,
и при
,
и при
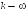
 (3) что означает
выполнение (1). Пусть
(3) что означает
выполнение (1). Пусть
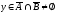 .
Тогда из
.
Тогда из
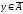 и (3) следует, что
и (3) следует, что
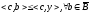 ,
а из
,
а из
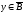 и (3) следует, что
и (3) следует, что
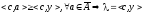 ч.т.д.
ч.т.д.
Теорема
2.
Пусть
A,B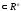 ;
A,B
;
A,B

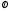 ,выпуклые
замкнутые, одно из них ограничено и
A
,выпуклые
замкнутые, одно из них ограничено и
A B=
B=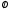 .
Тогда A
и B
строго отделимы. Если они оба ограничены,
то отделимость будет сильной.
.
Тогда A
и B
строго отделимы. Если они оба ограничены,
то отделимость будет сильной.
Пусть
заданы матрица B
размерности s n
и вектор
n
и вектор
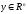 ,
причем
,
причем
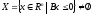 .
.
Теорема
3 (Фаркаша).
Неравенство <y,x>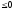 выполняется
выполняется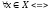 ,если
,если

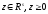 ,
что
,
что
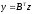 .
.
Доказательство:
Необходимость.
Пусть
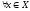 <y,x>
<y,x>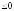 .
Докажем, что
.
Докажем, что
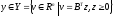 .
Пусть
.
Пусть
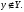 Y-
замкнуто и выпукло (замкнутость следует
из непрерывности линейных функций). По
Т.2
Y-
замкнуто и выпукло (замкнутость следует
из непрерывности линейных функций). По
Т.2
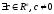 ,
что
,
что

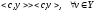 (4)
(4)
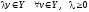 .
Из (4) =>
.
Из (4) =>
 ,
,
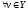 и
и
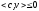 .
Но
.
Но
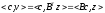
Значит

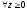 и
и
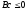 (5)
(5)
Т.к.
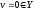 ,
то
,
то
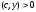 (6)
(6)
Положив
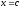 из (5) и (6) получаем противоречие условиям
теорем.
из (5) и (6) получаем противоречие условиям
теорем.
Достаточность.
Пусть
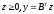 .
Тогда
.
Тогда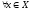
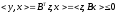 .
ч.т.д.
.
ч.т.д.
-
Свойства выпуклых функций.
Опр.1.
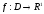 ,
где
,
где
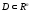 выпуклое множество, называется выпуклой
на этом множестве, если
выпуклое множество, называется выпуклой
на этом множестве, если
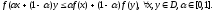 (1)
(1)
Замечание.
1)
Если в (1) при
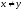 равенство
выполняется только для
равенство
выполняется только для
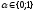 ,
то f-строго
выпуклая.
,
то f-строго
выпуклая.
2) f-вогнута, если – f - выпукла.
Теорема
1 (неравенство Иенсена).
Если
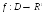 ,
,
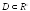 выпуклые, то
выпуклые, то
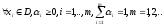
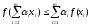 (2)
(2)
Доказательство (по индукции).
При
m
= 2 (2) следует из О.1. Пусть (2) справедливо
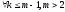 .
Пусть
.
Пусть
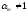 .
.
Тогда
 Пусть
Пусть
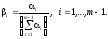 .
Тогда
.
Тогда
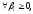
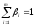 ,
,
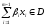 и
и
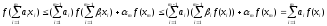 .
.
Теорема
2.
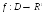 ,
где
,
где
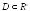 выпукло, является выпуклой
выпукло, является выпуклой

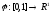 определенная формулой
определенная формулой
 ,
является выпуклой.
,
является выпуклой.
Доказательство.
Необходимость.
f
– выпуклая на D.
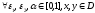
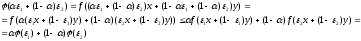 Достаточность.
Пусть
Достаточность.
Пусть
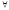 пары точек из D
и
пары точек из D
и
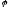 - выпуклая =>
- выпуклая =>
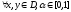
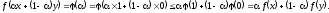
Теорема
3.
Пусть
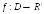 ,
,
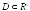 выпукла на D.
Тогда она непрерывна в
выпукла на D.
Тогда она непрерывна в
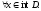
Теорема
4:
Если
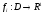 выпуклые
на
выпуклые
на
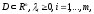 то
то
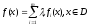 выпуклая.
выпуклая.
Доказательство:


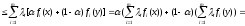
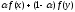
Теорема
5:
Если
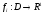 выпуклая на
выпуклая на
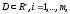 то
то
 выпукла.
выпукла.
Доказательство:
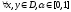

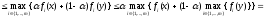
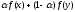
Замечание:
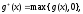
 выпукла
, если g(x) выпукла.
выпукла
, если g(x) выпукла.
Теорема
6:
Если

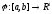 неубывающая и выпукла, а
неубывающая и выпукла, а
 выпукла на
выпукла на
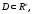 то
то
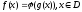 выпукла.
выпукла.
Доказательство:
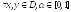
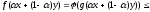
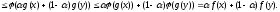
-
Критерии выпуклости функций.
Рассмотрим гладкие функции.
Теорема
1(Первый критерий):
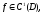 где
где
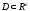 выпукло,
является выпуклой функцией
выпукло,
является выпуклой функцией

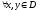 .
.
Доказательство:
Необходимость:
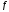 -
выпукла на
-
выпукла на
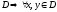 и
и
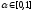
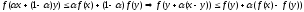
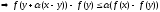 и
применяя формулу
и
применяя формулу
 к
последнему неравенству имеем
к
последнему неравенству имеем
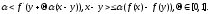 Разделив
его на
Разделив
его на
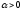 и
устремив
и
устремив
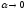 получаем
получаем
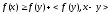 .
.
Достаточность:
Пусть
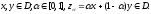 Из исходного неравенства
Из исходного неравенства
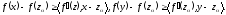 Первое умножается на
Первое умножается на
 ,
второе на
,
второе на
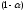 и складываем их:
и складываем их:
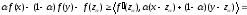
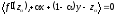
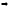
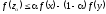 .
ч.т.д.
.
ч.т.д.
Теорема
2 (Второй критерий)
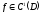 ,
где
,
где
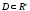 выпукло, является выпуклой функцией
выпукло, является выпуклой функцией
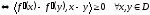 .
.
Теорема
3 (критерий выпуклости дважды
дифференцируемой функции)
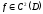 ,
где
,
где
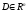 выпукло, является выпуклой функцией,
если
выпукло, является выпуклой функцией,
если
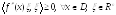 ,
(1)
,
(1)
И
если
 ,
то это условие является необходимым.
,
то это условие является необходимым.
Доказательство:
Необходимость:
Пусть
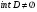 ,
,
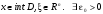 ,
что
,
что
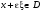 ,
если
,
если
 .
Из Т.2 и формулы
.
Из Т.2 и формулы
 следует
следует
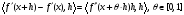 (2).
Сокращая
(2) на
(2).
Сокращая
(2) на
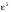 и
и
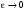 получим (1). Если
получим (1). Если
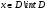 ,
то т.к. в выпуклом множестве нет
изолированных точек
,
то т.к. в выпуклом множестве нет
изолированных точек
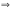
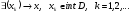 и
и
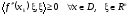 .
Переходя к
.
Переходя к
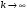 получим (1) для
получим (1) для
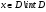 .
.
Достаточность.
Пусть
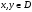 и
и
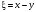 .
Из (1) и формулы
.
Из (1) и формулы
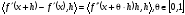 следует
следует ,
т.е. для
,
т.е. для
 выполнены
условия Т.2.
ч.т.д.
выполнены
условия Т.2.
ч.т.д.
