11. Теорема Куна-Таккера.

Дополнительные условия, сформулированные Куном-Таккером в различных по постановкам теоремам являются обобщением принципа Лагранжа. Рассмотрим случай задачи ВП. Тогда . (1)

Опр. 1. Множество (1) называется регулярным (выполнение условия Слейтера), если такая, что .

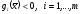Замечание. Для выполнения условия Слейтера достаточно потребовать: что . Тогда из выпуклости , а из выпуклости .

Теорема 1 (Куна-Таккера). Пусть в задаче ВП , выполнено условие регулярности и . Тогда вектор такой, что является седловой точкой функции Лагранжа для этой задачи.

Доказательство

Рассмотрим в

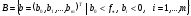. Покажем: . Пусть , что . Если . Если , что .

- выпуклы! - т.к. оно пересечение конечного числа полупространств. Покажем для . Пусть , что

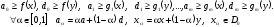
Из выпуклости

И выпукло.

Из (Т.1, п.2.4) 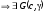- гиперплоскость, отделяющая . Обозначим

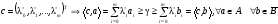(2) Покажем: Действительно, пусть

(очевидно) Тогда

(2) перепишется: (3)Из (3) выведем: , где удовлетворяет условиям (Т.4.1.1) и является Седловой точкой.

Пусть положим . Из левой части (3) для получаем Из правой части (3) Значит (4)

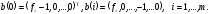
В рассмотрим Подставляя в правую часть (3), получим:Покажем, что Пусть точка, фигурирующая в условиях Слейтера, тогда Для из левой части (3) находим (5)

Предположим, Тогда, т.к. из условий Слейтера следует . Это противоречит (5), т.е. значит Поделив на можно считать Осталось показать, что (6)

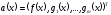Пусть Для выполняется С учетом из левой части (3) для этой точки получим и в силу (4) получаем условие (6).

Замечание. При 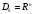задача ВП является частным случаем задачи 1 (П.3.1). Предположим, что в задаче ВП . Тогда условие 1 в (Т.1., п.4.2) принимает вид и из теоремы Куна-Таккера вытекает теорема Кароша-Джона, в которой Обратно, если в задаче ВП некоторая точка удовлетворяет условиям (Т.1, п.1.3) при 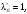то по Т.,п.4.2 пара является седловой точкой функции Лагранжа этой задачи и по Т.2, п.4.2 точка доставляет решение задаче ВП.

12. Связь между основной и двойственной задачами.

Пусть - функция Лагранжа для задачи ВП. Введем в рассмотрение функцию ,

Тогда и при неравенство переходит в равенство. Если то либо , что либо , что . В любом случае выбором можно сделать сколь угодно большой, поэтому и .

Поэтому исходная задача может быть записана в виде:

Задача 1. .

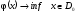Поступим аналогичным образом, поменяв роль переменных и операций максимизации и минимизации, т.е. введем наряду с функцией функцию , определенную формулой и рассмотрим задачу.

Задача 2. .

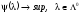Опр. 1. Задача 2 называется двойственной к задаче 1, которая называется основной. Переменные 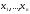называются основными, а двойственными. В качестве примера рассмотрим следующую задачу:

, (1) где А – матрица размерности . Она называется задачей линейного программирования в канонической форме. Для этой задачи,а функция Лагранжа имеет вид:.

Функция выписывается в явном виде

Отсюда ясно, что точку , на которой может достигаться верхняя грань функции , достаточно искать во множестве . Двойственная задача к задаче (1) формулируется следующим образом: (2). Таким образом, двойственная задача к задаче (1) тоже является задачей линейного программирования. Можно показать, что двойственная задача к задаче (2) будет исходной задачей (1).

Замечание. В общем случае задача двойственная к двойственной не всегда совпадает с исходной.

Задачи 1 и 2 из предыдущего пункта тесно связаны между собой. Обозначим .

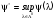Теорема 1. Имеет место неравенство .

Доказательство

Переходя в последнем неравенстве к нижней грани по , получим искомое неравенство

.

Замечание. Существуют задачи ВП, для которых .

Теорема 2. Для того, чтобы было выполнено (1) необходимо и достаточно, чтобы функция Лагранжа имела седловую точку на множестве . Множество Седловых точек функции Лагранжа совпадает с .

Доказательство

Необходимость. Пусть выполнено (1). Покажем, что пара является седловой для функции Лагранжа имеем (2)

Т.к. из (2) следует (3). Последнее равенство означает, что .Таким образом, пара - седловая точка и множество принадлежит множеству точек функции Лагранжа.

Достаточность. Пусть - седловая точка функции Лагранжа. Тогда

(4). Аналогично, из неравенства (5). Из (3) и (5) с учетом Т.1 получаем .

Тогда .

Отсюда выводим, что множество седловых точек функции Лагранжа принадлежит множеству .

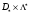Теоремы 1 и 2 в совокупности образуют теорему двойственности.

Замечание. Если задача линейного программирования имеет решение, то для нее существует седловая точка функции Лагранжа. Тогда по Т.2 двойственная задача имеет решение и значения целевых функций этих точек совпадают.