Задача линейного быстродействия.

В линейных задачах Теории оптимального уравнения дифференциальное уравнение принимает вид (*), где A(t) – где квадратная матрица , B(t) – матрица, W(t) – вектор , а функции 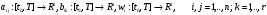непрерывна по t. К уравнению (*) можно перейти непосредственно моделируя реальный динамический объект, а также в результате линеаризации дифференциальных уравнений его движения, когда исходная модель не линейна.

Линейную задачу теории оптимального уравнения называют задачей линейного быстродействия, если

уравнение (*) однородно, т.е. W(t)=0, а A и B – постоянные;

минимизируемый функционал имеет форму Лагранжа при ;

начальный момент фиксирован;

конечный момент не фиксирован;

левый и правый концы траектории закреплены, т.е. , ;

фазовые ограничения отсутствуют, ;

область изменения управляющих параметров имеет вид:

, ограничена, содержит в себе точку O, которая не является для нее угловой; U – выпуклый ограниченный многогранник.

Опр.1 Подпространство называется инвариантным относительно линейного преобразования , если Оно называется собственным, если не совпадает со всем .

Замечание: принадлежит инвариантному подпространству относительно линейного преобразования A в том и только том случае, если - линейно зависимы.

Опр.2 В задаче линейного быстродействия выполнено условие общности положения, если для любого вектора w, параллельно какому-либо ребру U, вектор Bw не принадлежит никакому собственному инвариантному подпространству относительно линейного преобразования A, т.е. линейно независимы.

Для задачи линейного быстродействия дифференциальное уравнение движения имеет вид (1), минимизируемый функционал , функция Гамильтона-Понтрягина при 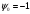. (2) и система сопряженных уравнений (3).

Лемма1. Пусть уравнение на - порожденное им движение и - решение сопряженного уравнения (3). Тогда (4)

Лемма2. Пусть - нетривиальное решение уравнения (3). Для того, чтобы вектор принадлежал собственному инвариантному относительно преобразования A подпространству, достаточно выполнения равенства при некотором .

Достаточные условия оптимальности в задаче линейного быстродействия.

Теорема1 (достаточное условие оптимальности). Пусть в задаче линейного быстродействия выполнены условия общности положения, и пара удовлетворяет условиям принципа максимума при 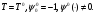Тогда - минимально возможное время перевода фазового вектора из начального положения в начало координат, - оптимальное управление, - оптимальная траектория.

Доказательство. От противного приходим к существованию управления , , приводящего фазовый вектор из в в начало координат в

Пусть (5)

Тогда (6)

Из принципа максимума следует

(7).

Из (6) (8)

Из леммы 1 и (8):

(9)

Из (7) и (9) (10) С другой стороны т.к. 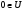, то справедливо неравенство (11)

и поэтому (12) Из (10) и (12) =0. Но из (12) а из (11) Обозначим грань наименьшей размерности многоугольника U, которая содержит начало координат. 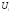либо совпадает с U, либо является гранью U, но во всяком случая, размерность не меньше 1, т.к. начало координат не вершина U, а внутренняя для . 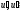линейная функция , определяемая формулой , , достигает максимального значения 0 во внутренней точке (начале координат), и поэтому постоянна на В частности, если - концы какого либо ребра грани 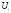, то Следовательно, для вектора направленному по ребру многогранника U, Из леммы 2 следует, что вектор Bu принадлежит собственному инвариантному относительно преобразования A подпространству, а это противоречит условию общности положения. Итак, предположение приводит к противоречию.

Теорема 2 позволяет выяснит структуру оптимального управления в задаче линейного быстродействия.

Теорема2 (о числе переключений). Пусть в задаче линейного быстродействия включено условие общности положения. Тогда для любого нетривиального решения сопряженной системы дифференциальных уравнений (3) на промежутке функция , найденная из условия , (13)

кусочно-постоянная и ее значения являются вершинами U.

Замечание. Из теоремы 2 следует, что число переключений конечно, но произвольно. При дополнительных предположениях число переключений допускает точную оценку.

Теорема3 (А.А. Фельдбаума). Пусть в задаче линейного быстродействия множество и все собственные значения матрицы A действительны. Тогда для всякого нетривиального решения сопряженной системы дифференциальных уравнений (3) каждая компонента вектор-функции , найденная из условия (13), кусочно-постоянная; принимает только значения и имеет не более n-1 переключений, где n-размерность фазового вектора.