Общая постановка задачи оптимального управления.

В задачах оптимального управления характерно наличие динамического объекта (меняющегося во времени).Положение его характеризуется в каждый момент времени фазовым вектором . Предполагается, что вектором управляющих параметров можно управлять (влиять) на движение объекта. Зависимость от отличается для различных объектов и может описываться, например, системой дифференциальных уравнений

, где (1) описывает внутреннее устройство объекта и воздействие внешних факторов. Обычно предполагается, что (2) в каждый момент времени, - текущее время, - заданное множество. Кроме (2) на могут быть наложены ограничения на зависимость от времени. Обычно - замкнуто. Таким образом определяется класс допустимых уравнений: гладкие, непрерывные, кусочно-непрерывные, и т.д. функции.

Предполагается, что задан начальный момент и множество - допустимых начальных состояний объекта, и желательно так им управлять, чтобы в конечный момент объект перешел на некоторое множество заданных допустимых конечных состояний. Считаем, что допустимое управление переводит объект из в на отрезке времени , если соответствующее этому управлению фазовое состояние объекта 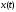удовлетворяет условиям . (3)

Замечание. 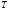может быть не фиксированным, а определяться из условия попадание вектора на .

Обычно предполагается, что каждому допустимому управлению 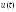, заданному на и соответствующей ему траектории объекта сопоставлено некоторое число 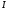, оценивающее качество пары ,, т.е. задан некоторый функционал, или критерий, качества , имеющий, например, вид (4)

Замечание. Из в управляемый объект часто можно привести различными способами и желательно выбрать лучший в некотором смысле переход.

Задачу оптимального управления можно сформулировать так: среди допустимых управлений выбрать такое и соответствующую ему траекторию объекта , переводящую объект из множества начальных состояний на множество конечных состояний , что при этом функционал качества принимает минимальное значение, т.е. , где минимум берется по всевозможным допустимым управлениям и соответствующим траекториям , переводящим объект из на .

Достаточное условие существования решения задачи оптимального управления.

Сформулируем достаточные условия существования решения задачи оптимального управления следующего вида:

,

.

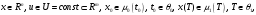
Относительно данных сделаем предположения:

1) - компактно;

2) мн-во компактно;

3) множество выпукло для всех ;

4) существует константа , для которой справедливо неравенство .

Класс допустимых уравнений отождествляется с функциями, интегрируемыми по Лебегу на интервале управления.

Теорема 1. Пусть выполнены предположения 1) - 4) и множество . Тогда существует четверка , на которой функционал достигает минимума.

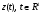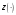Замечание 1. В теории оптимального управления часто применяют следующие обозначения. Если некоторая функция, то ее значение в точке , а - сама функция, как элемент функционального пространства.

Замечание 2. Если функционал качества управления имеет вид , где . Первое слагаемое называется интегральным, а второе терминальным, а сам функционал – функционалом Больца. Если , то получаем функционал Майера, а в случае - функционал Лагранжа.