Постановка вариационной задачи с подвижными границами.

Пусть в простейшей вариационной задаче точки A и B находятся на кривых (1)

Функция y допустима, если удовлетворяет условиям допустимости в простейшей вариационной задаче, а граничные точки выбираются произвольно на кривых, определяемых (1). Минимизируемый функционал имеет нефиксированные пределы интегрирования.

Рассмотрим задачу:

Рассмотрим сначала случай удовлетворяет уравнению: 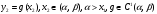. Функционал обозначим: - класс допустимых функций в простейшей задаче вариационного исчисления, в которой

Теорема 1. Если - решение задачи с подвижным правым концом, то необходимо (2)

(3)

Доказательство:

-решение простейшей задачи для и (2) имеет место. Пусть

Т.к. , то , что Пусть такая, что - непрерывно дифференцируемое расширение на

принадлежит

Положим

Т.к. , то в достигает локального минимума и

+ (4)

.

Т.к. удовлетворяет дифференциальному уравнению Эйлера-Лагранжа, отвечающему основной функции , то

(5)

А (6)

Преобразуя (4) с учетом (5) и (6), получаем

Равенство (3) называют условием трансверсальности на правом конце. Если правая кривая (граница) имеет уравнение , , то оно принимает вид

Аналогично можно рассмотреть случай незакрепленного левого конца или обоих концов.

Задача Больца

Если в задаче с подвижными границами зависимость минимизируемого функционала явная от границ, т.е. (1),где - дважды непрерывно дифференцируемые функции, то вариационную задачу называют задачей Больца. Пусть в задаче Больца левый конец фиксирован, тогда учитывая результаты п.11.1 выведем условие трансверсальности на правом конце.

(2) и (3) в силу (2) сводится к . (4)

Покажем, что уравнение Эйлера-Лагранжа для (4) определяется лишь интегральным слагаемым в (3).

.

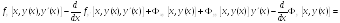
Используя ((3) п.11.1) условия трансверсальности для (4) примут вид

, откуда находим

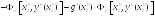. (5)

Если кривая правой границы , то (5) принимает вид . Аналогично можно рассмотреть случай незакрепленного левого конца и обоих концов.

Изопериметрическая задача.

На множестве допустимых функций накладывается условие: функционал, заданный на множестве допустимых функций (как и минимизируемый) должен принимать фиксированное значение на любой допустимой функции.

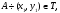
Пусть - открытое выпуклое множество, , , Функцию назовем допустимой , если , , , , . Каждой поставим в соответствие число . Требуется минимизировать функционал I на . В случае изопериметрическая задача имеет вид: .

, , .Пусть Для рассмотрим функционал .

Теорема 1. Если решение изопериметрической задачи, то найдется что удовлетворяет уравнению Эйлера-Лагранжа, соответствующему функционалу , т.е. .

Доказательство. не стационарная функция для (иначе ). Пусть , Такая найдется, т.е. не стационарная для . Рассмотрим двухпараметрическое семейство функций

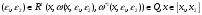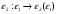Причем , i=1,2, . Для малых по абсолютной величине . Положим. Видно что , i=1,2. и по теореме о неявной функции уравнение определяет функцию в окрестности точки . При этом . из малой окрестности О (1) и дифференцируя обе части (1) по получаем (2). Откуда с учетом получаем (3)

Рассмотрим однопараметрическое семейство функций

где малая окрестность нуля. Из следует , что значит , а и достигает минимума при . Тогда и с учетом (3) получаем

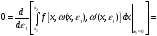
(4)

. Пусть , тогда из (4) , что означает и интегрируя по частям получаем , при (5). Тогда из леммы Лагранжа .

Замечание: интегральные кривые уравнения Эйлера-Лагранжа называют экстремалями. Экстремум может достигаться только на них. Из Т.1, если не экстремаль для , то можно сразу взять .