2.14. Неравенство Клаузиуса

Всякое механическое движение материальных тел согласно законам классической механики имеет свойство обратимости.

Всегда возможно обратное движение, т. е. движение, при котором тело проходит все те же точки пространства с теми же скоростями, что и в прямом движении.

Обратимость механического движения вытекает из их симметрии по отношению к замене будущего прошедшим.

Относительно тепловых процессов этого сказать нельзя.

Все тепловые процессы необратимы, так как физическая система, предоставленная самой себе, всегда стремится перейти в состояние термодинамического равновесия.

Известно, что все тепловые явления сводятся к механическому движению атомов и молекул тел.

Поэтому необратимость тепловых процессов как бы находится в противоречии с обратимостью механического движения.

Установлено, что необратимость тепловых процессов имеет вероятностный характер.

Самопроизвольный переход физической системы из равновесного состояния в неравновесное, невозможен или, как говорят, менее вероятен, чем переход из неравновесного состояния в равновесное состояние.

При этом надо помнить, что всегда возможны флуктуации.

В 1850 г. Клаузиус, используя теорему Карно о максимальном КПД идеального цикла, получил неравенство (неравенство Клаузиуса), которое выражает важную теорему термодинамики, т. е. для кругового процесса

, (2.54)

где dQ – количество теплоты, сообщенное физической системе (или отводимое от нее) на бесконечно малом отрезке кругового цикла;

Т – абсолютная температура соответствующего элемента cреды;

– элементарная приведенная теплота.

Если процесс квазистатический, то неравенство Клаузиуса переходит в равенство Клаузиуса

. (2.55)

2.15. Энтропия

Для описания термодинамических процессов широко используется понятие энтропии.

Отношение (приведенное количество теплоты) в обратимом процессе является полным дифференциалом и есть функция состояния системы, называемаяэнтропией S. Это непосредственно следует из равенства Клаузиуса, т. е.

. (2.56)

Докажем, что в любом обратимом круговом процессе

. (2.57)

Для доказательства рассмотрим идеальный газ. Согласно первому началу термодинамики

. (2.58)

Используя уравнение Менделеева – Клапейрона перепишем (13.58) в виде

. (2.58^*)

В обратимом процессе при переходе идеального газа из состояния 1 в 2 интеграл не зависит от вида процесса перехода из 1 в 2, т. е.

(2.59)

или

. (2.60)

В случае кругового процесса V₂ = V₁, T₂ = T₁, то для идеального газа

.

Что же произойдет с энтропией системы?

Из анализа формул (13.58) и (13.58*) следует, что

(2.61)

или

. (2.62)

При неизменном числе молей идеального газа

.

После логарифмирования

(2.63)

или

С учетом последнего равенства формула (13.62) принимает вид

(2.64)

или

. (2.65)

При нагревании тела (dQ  0) его энтропия возрастает (dS  0); при охлаждении (dQ  0) энтропия тела убывает (dS  0). В процессе завершения обратимого цикла dS = 0, т. е. S = сonst.Энтропия изолированной системы в любом обратимом процессе остается постоянной.

Таким образом, энтропия физической системы есть функция ее состояния, и определяется с точностью до произвольной постоянной.

Разность энтропии в двух равновесных состояниях 1 и 2 равна приведенному количеству тепла, которое необходимо сообщить системе, чтобы перевести ее из состояния 1 в 2 по любому квазистатическому пути.

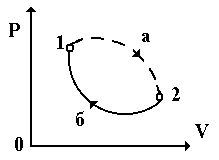
Рассмотрим физическую систему, которая необратимо переходит из равновесного состояния 1 в равновесное состояние 2 (рис. 2.11).При необратимом процессе перехода системы (на рис. 13.11 он изображен пунктирной линией 1– а – 2) из состояния 2, она переходит квазистатически по какому-либо пути, например, 2 – б – 1.

На основании неравенства Клаузиуса (10.54), имеем

. (2.66)

Учитывая, что процесс (2–б –1) – квазистатический

, (2.67)

тогда неравенство Клаузиуса принимает вид

, (2.68)

где Т – абсолютная температура окружающей среды, которая отдает физической системе тепло dQ.

Рис. 2.11

В случае адиабатически изолированной системы, для которой dQ = 0, в формуле (2.67) интеграл обращается в нуль, т. е.

S₂  S₁. (2.69)

Неравенство (13.69) выражает закон возрастания энтропии.

Следовательно, энтропия адиабатически изолированной системы не может убывать; она либо возрастает (необратимый процесс), либо остается постоянной (обратимый процесс). Понятие энтропии носит двойственный характер – макроскопический и микроскопический. Соотношение = dS является макроскопическим определением энтропии.

Свойства энтропии.

1. Энтропия системы равна сумме энтропии каждого тела, т. е.

.

2. Энтропия – функция состояния системы.

3. В равновесных процессах без передачи тепла энтропия физической системы не меняется.

4. Энтропия является монотонно возрастающей функцией внутренней энергии тела (при постоянном объеме).

5. При постоянном объеме (изохорический процесс)

dQ = dU,

т. е.

Так как Т  0, то dS и dU имеют один и тот же знак.

Задание внутренней энергии тела как функции объема и энтропии полностью определяет свойства однородного тела,

т. е.

U = U(V, S).

6. Энтропия определяется с точностью до произвольной постоянной.