1.14. Космические скорости. Законы Кеплера
После длительной обработки многолетних наблюдений астронома Тихо Браге за движением планет Солнечной системы Кеплер эмпирически установил три закона движения планет:
Каждая планета движется по эллипсу, в одном из фокусов которого расположено Солнце.
Радиус-вектор планеты в равные промежутки времени описывает равные площади.
Квадраты периодов обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца.
Используя законы движения планет Солнечной системы, установленных Кеплером, Ньютон открыл закон всемирного тяготения.
Используя теорию движения планет Солнечной системы можно рассчитать траекторию движения искусственных спутников Земли и космических кораблей с выключенными двигателями (без учета сопротивления атмосферы Земли и гравитационного притяжения спутников – кораблей со стороны Солнца, Луны и других планет).
Полная энергия спутника в поле тяготения Земли равна
W = Wk + Wp,
т. е.
где m, M – массы спутника и Земли соответственно; v – скорость спутника;
r – расстояние до него.
Если W < 0, то движение финитно и происходит по эллиптической орбите. В случае кругового движения
.
Следовательно, первая космическая скорость при r = RЗ
V1 7,9 км/c. (29)
Минимальное значение энергии W, при котором движение спутника становится инфинитным (траектория – парабола ), равно нулю,
т. е.
Тогда вторая космическая скорость
11,2
км/c. (30)
3. Если полная энергия спутника положительна, то его движение станет гиперболическим и третью космическую скорость можно найти из условия
где
МС
–
масса Солнца. Тогда
42 км/с.
В
направлении движения Земли
16,7 км/c. В направлении противоположном
движению Земли третья
космическая скорость
72,7 км/c.
1.15. Упругие и неупругие столкновения
В физике под термином столкновения понимают не просто непосредственный удар, например, бильярдных шаров, а процесс в более широком смысле.
Столкновениями, или ударом, называют любые кратковременные взаимодействия частиц (тел).
Особенностью теории столкновений является то, что при этом детально не анализируются механизмы взаимодействия. Причина заключается в том, что анализ сил, возникающих при столкновении, весьма затруднителен, а во многих случаях и просто невозможен, и не только из-за малого промежутка времени процесса взаимодействия. Например, так обстоит дело с ядерными силами.
После столкновения частицы в конечном состоянии могут отличаться по своим внутренним свойствам от частиц в начальном состоянии.
В связи с этим различают упругие и неупругие столкновения.
Столкновениями обусловлены многие явления, рассматриваемые в различных разделах физики. Прежде всего, столкновения играют основную роль в структуре и динамике плазмы и газов.
Такие процессы, как передача тепла в газах, диффузии газов и другие, определяются свойствами сталкивающихся молекул и других частиц друг с другом. Свойства атомов, атомных ядер, и элементарных частиц можно исследовать одним из основных способов, изучая и анализируя их столкновения с другими частицами.
Для описания процесса взаимодействия привлекают законы сохранения. Поскольку законы сохранения справедливы не только в классической, но и в квантовой механике, то результаты, полученные из этих законов, применимы и к столкновениям квантовых частиц, например, атомов, ядер и др. частиц.
Рис. 16
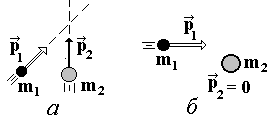
Систему отсчета, в которой столкновения частиц изучаются на опыте, называют лабораторной (Л.С.). Иногда в этой системе отсчета одна из частиц
Рис. 17
Система отсчета, в которой центр инерции покоится, а суммарный импульс частиц системы равен нулю, называют системой центра инерции.
В такой системе отсчета векторы импульсов сталкивающихся частиц равны по величине и противоположны по направлению.