1.4. Мощность. Коэффициент полезного действия в механике

На практике важно знать, как быстро машина или механизм совершают работу.

Быстрота совершения работы характеризуется мощностью.

Cредняя мощность численно равна отношению работы к промежутку времени, за который совершается работа.

<N> = DA/Dt. (6)

Если Dt ® 0, то, перейдя к пределу, получим мгновенную мощность:

(7)

или

. (8)

, (9)

или

N = Fvcos.

В СИ мощность измеряется в ваттах (Bт).

На практике важно знать производительность механизмов и машин или другой промышленной и сельскохозяйственной техники.

Для этого используют коэффициент полезного действия (КПД) .

Коэффициентом полезного действия называют отношение полезной работы ко всей затраченной.

. (10)

или

.

1.5. Кинетическая энергия

Энергию, которой обладают движущиеся тела, называют кинетической энергией (W_k).

Найдем полную работу силы при перемещении м. т. (тела) на участке пути 1– 2. Под действием силы м. т. может изменять свою скорость, например, увеличивает (уменьшает) от v₁ до v₂.

Уравнение движения м. Т. Запишем в виде

Полная работа 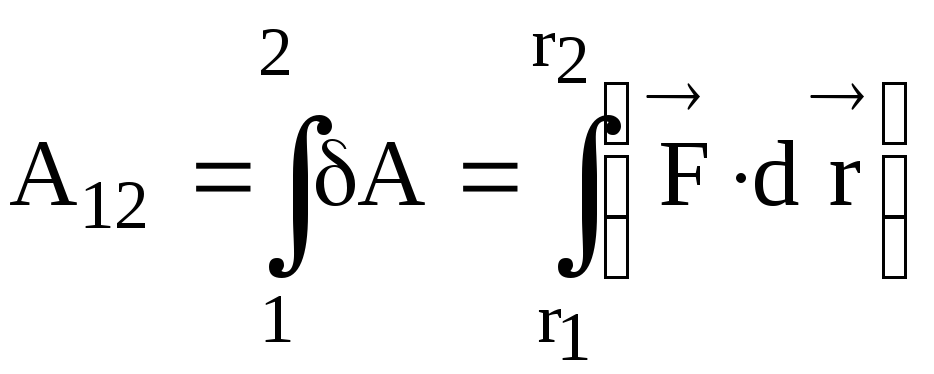или.

После интегрирования ,

где называют кинетической энергией. (11)

Cледовательно,

. (12)

Вывод: Работа силы при перемещении материальной точки равна изменению ее кинетической энергии.

Полученный результат можно обобщить на случай произвольной системы м. т.: .

Следовательно, суммарная кинетическая энергия – величина аддитивная. Широкое применение имеет другая форма записи формулы кинетической энергии: . (13)

Замечание: кинетическая энергия – функция состояния системы, зависит от выбора системы отсчета и является величиной относительной.

В формуле А₁₂ = W_k под А₁₂ надо понимать работу всех внешних и внутренних сил. Но сумма всех внутренних сил равна нулю (на основании третьего закона Ньютона) и суммарный импульс равен нулю.

Но не так обстоит дело в случае кинетической энергии изолированной системы м. т. или тел. Оказывается, что работа всех внутренних сил не равна нулю.

Рис. 6

Достаточно привести простой пример (рис. 6).

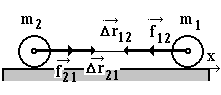
Как видно из рис. 6, работа силы f₁₂ по перемещению м. т. массой m₁ положительна

A₁₂ = (– f₁₂) (– r₁₂) > 0

и работа силы f₂₁ по перемещению м.т. (тела) массой m₂ также положительна:

A₂₁ = ( + f₂₁) ( + r₂₁) > 0.

Следовательно, полная работа внутренних сил изолированной системы м. т. не равна нулю:

А = А₁₂ + А₂₁  0.

Таким образом, суммарная работа всех внутренних и внешних сил идет на изменение кинетической энергии.