
РАСЧЕТНО-ГРАФИЧЕСКИЕ ЗАДАНИЯ
Расчетно-графическое задание 01 ПЛОСКОСТЬ
Цель – закрепить знания следующих разделов курса начертательной геометрии и инженерной графики:
Правила оформления графических работ (ГОСТ 2.301-68, ГОСТ
2.303-68, ГОСТ 2.304-81, ГОСТ 2.104-68).
Координатный способ построения чертежа точки, прямой и плоскости.
Взаимопринадлежность точки, прямой, плоскости.
Взаимное расположение прямых и плоскостей.
Взаимное расположение двух плоскостей.
Главные линии плоскости.
Взаимоперпендикулярность прямых и плоскостей.
Определение видимости на чертеже.
Определение натуральной величины отрезка прямой.
Содержание работы
Задача 01.01. Оформить титульный лист (рис. 2).
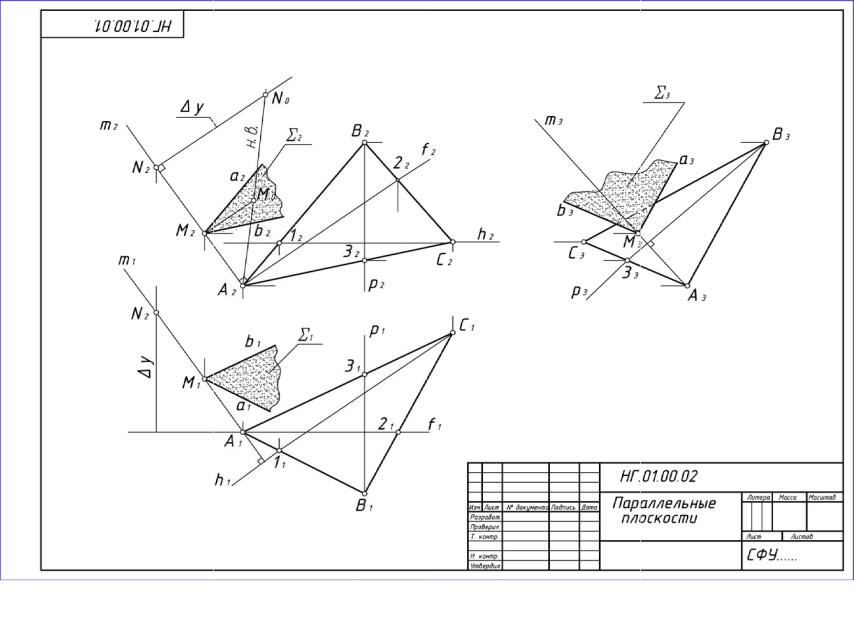
Задача 01.02. Построить плоскость, параллельную плоскости треугольника АВС и удаленную от этой плоскости на 30 мм.
Задача 01.03. Построить линию пересечения двух непрозрачных пластин – треугольника АВС и четырехугольника КЕDH. Определить видимость сторон многоугольников и KEDH.
6
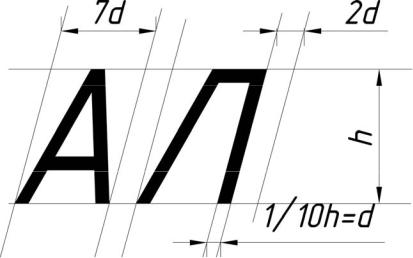
Методические рекомендации к выполнению задачи 01.01
Все надписи на титульном листе должны быть выполнены чертежным шрифтом в соответствии с ГОСТ 2.304-81 (тип Б с наклоном). Буквы и цифры рекомендуется вписывать в предварительно вычерченную тонкими линиями вспомогательную сетку (рис. 1).
Рис. 1
При защите титульного листа студент должен знать ответы на следующие вопросы:
Что называют форматом?
Каково обозначение основных форматов в соответствии с ГОСТ
2.301-68?
На что указывают цифры в обозначении формата?
Каковы размеры сторон основных форматов, установленных ГОСТ 2.301-68?
Что называют размером шрифта?
Какие размеры шрифта устанавливает ГОСТ 2.304-81?
Чем отличаются шрифты типа А и типа Б?
От чего зависят параметры букв и цифр чертежного шрифта?
Каков угол наклона букв и цифр наклонного шрифта?
Чему равна ширина большинства букв строчного шрифта?
Какой должна быть высота цифр в тексте?
Каково расстояние между буквами в словах и цифрами в числах?
7

8
Рис. 2
Все задачи начертательной геометрии решаются в пространстве, поэтому очень важно правильно изображать прямую, плоскость и их сочетание. Для построения плоскости предполагается, что она может быть построена, если найдены элементы, определяющие ее положение в пространстве, т. е. можно построить плоскость, проходящую через три заданные точки, через прямую и точку вне ее, через две пересекающиеся или две параллельные прямые. Также предполагается, что если даны две пересекающиеся плоскости, то можно найти линию их пересечения.
Будем считать, что прямая и плоскость в пространстве бесконечны и задавать прямую можно отрезком, а плоскость – ограниченным участком правильной или неправильной формы.
Способность пространственного представления приобретается не сразу, а вырабатывается в процессе основательного изучения теоретического материала, самостоятельного решения задач и анализа задач, решенных другими.
Методические рекомендации к выполнению задачи 01.02
Прежде чем приступить к решению задачи 01.02 (построение параллельной плоскости (рис. 3)), необходимо выполнить следующую подготовительную работу:
1. Расположив формат А3 (297 420) так, чтобы поле подшивки (20 мм слева) было вдоль короткой стороны формата, вычертить:
рамку;
в верхнем правом углу рамки – таблицу координат размером
40 80;
в нижнем правом углу рамки основную надпись (55 185) (рис. 4);
оси координат x, y, z (начало координат 0 примерно в центре поля чертежа).
2. Построить проекции точек по заданным координатам (табл. 2). Примечание. Координатный способ построения проекций точек рас-
смотрим на примере точки А, имеющей координаты x = 30, y = 10, z = 20 (рис. 5).
9
10
Рис. 3
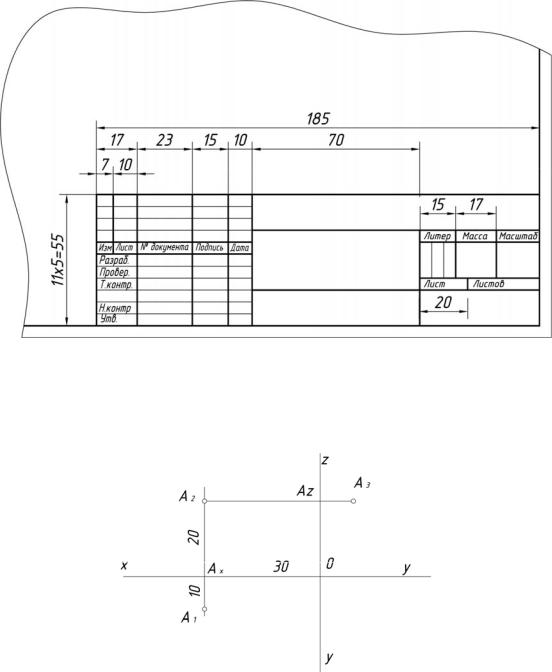
Рис. 4
Рис. 5
3. От начала координат О влево по оси ОХ (если координата x > 0) откладывают отрезок, длина которого равна координате х данной точки
(ОАх = 30).
4.Через полученную точку (Ах) проводят перпендикуляр к оси ОХ.
5.Отложив на проведенном перпендикуляре вниз от оси ОХ (если
координата y > 0) отрезок длиной, равной координате y(АхА1 = 10), получают горизонтальную проекцию точки (А1).
11
6.Отложив на этом же перпендикуляре вверх от оси ОХ (если коор-
дината z > 0) отрезок длиной, равной координате z(АхА2 = 20) получают фронтальную проекцию точки (А2).
7.Проведя перпендикуляр к оси ОZ через фронтальную проекцию
точки (А2) и отложив на нем от оси ОZ координату (АzA3 = 10) заданной точки, получают профильную проекцию точки (А3).
8.Таким же способом строят проекции всех остальных точек.
Эта задача относится к комплексным задачам, т. к. она состоит из ряда элементарных задач (построение прямой, перпендикулярной плоскости, отрезка прямой заданной длины, построение взаимнопараллельных прямых и плоскостей).
Решать ее целесообразно, разбив на отдельные этапы: анализ, составление плана решения, последовательные построения на чертеже.
Анализируя условие задачи, отмечаем, что искомый элемент (плоскость, параллельная данной) можно рассматривать как геометрическое множество точек, удаленных от данной плоскости треугольника АВС на расстояние 30 мм. Для построения такой плоскости необходимо найти, по крайней мере, одну такую точку в пространстве и затем, используя признак параллельности двух плоскостей (две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости), через полученную точку провести искомую плоскость, задав ее двумя пересекающимися прямыми, параллельными двум прямым данной плоскости.
План решения
1.Из произвольной точки заданной плоскости восстановить перпендикуляр к этой плоскости.
2.На перпендикуляре определить точку, удаленную от основания перпендикуляра на 30 мм.
3.Через построенную точку провести плоскость, параллельную заданной.
Последовательность построений
1.В заданной плоскости треугольника АВС задают:
горизонталь h (фронтальная проекция С212 = h2 OX, горизонтальная проекция h1 = C111);
фронталь f (горизонтальная проекция А121 = f1 OX, фронтальная проекция f2 = A222);
профильную прямую p (В131 = p1 OX, B232 = p2 OX, B333 = p3).
12
2. Из произвольной точки A треугольника АВС проводят перпендикуляр m к плоскости этого треугольника, причем:
горизонтальная проекция перпендикуляра m проходит через A1 под углом 90 к фронтальной проекции горизонтали (m1 h1,
A1 m1);
фронтальная проекция перпендикуляра m проходит через A2 под углом 90 к фронтальной проекции фронтали (m2 f2, A2 m2);
профильная проекция перпендикуляра m проходит через A3 под углом 90 к профильной проекции профильной прямой (m3 p3,
A3 m3).
3. Наперпендикуляреm находятточкуМнарасстоянии30 мм, дляэтого:отмечают произвольную точку N (N1 m1, N2 m2) и определяют натуральную величину расстояния от точки A до точки N, для чего строят прямоугольный треугольник ( А2N2N0), одним катетом которого является одна из проекций отрезка AN, например, A2N2, а вторым – разность расстояний концов отрезка A и N до соответствующей плоскости проекции (в данном случае до 2), например,y – разность расстояний проекций A1 и N1 до оси OX и N2N0 = y. Гипотенуза построенного треугольника (A2N0) равна натуральной
длине отрезка AN перпендикуляра m;
на гипотенузе A2N0 откладывают отрезок A2M0 = 30 мм и проводят M0M2 A2N2. A2M2 – фронтальная проекция перпендикуляра m, длина которого равна 30 мм, т. е. M2 – проекция точки M, удаленной от плоскости треугольника АВС на 30 мм. Проекции M1 и M3 определяют, проведя линии связи из M2 до m1 и m3 (M1 m1,
M3 m3).
4. Через точку M проводят прямые a и b, соответственно параллельные прямым, принадлежащим плоскости АВС, например, сторонам этого
треугольника АВ и АС (a1 A1B1, a2 A2B2, a3 A3B3, b1 A1C1, b2 A2C2, b3 A3C3), которые и определят искомую плоскость (a ∩ b).
Доказательство
Плоскость (a ∩ b) отвечает требованиям условий задачи. Действительно, плоскость (a ∩ b) параллельна заданной плоскости
треугольника АВС, т. к. ее определяют две пересекающиеся прямые a и b, параллельные соответственно прямым, принадлежащим плоскости треугольника АВС(a AB, b AC).
Далее, плоскость (a ∩ b) расположена на расстоянии 30 мм от заданной плоскости, т. к. она проходит через точку M, удаленную от этой плоскости на 30 мм. Это видно из построения.
13
Исследование
Задача может иметь два решения, т. к. можно построить две плоскости, параллельные данной и удаленные от нее на заданное расстояние.
Методические рекомендации к выполнению задачи 01.03
Решение задачи 01.03 (рис. 6) выполняют, предварительно вычертив рамку, основную надпись и проекции плоскости треугольника АВС ( А1В1С1, А2В2С2, А3В3С3) по тем же координатам точек, что и в задаче 01.02, а также проекции точек K, E, H и D, определяющих в дальнейшем плоскость четырехугольника (табл. 2).
Одна из вершин, например точка К, задана двумя координатами, поэтому получается только одна ее проекция. Остальные проекции определяются построением, для этого:
одноименные проекции точек с известными координатами, например D, E, H, соединяют отрезками прямых линий и получают проекции треугольника DEH – D1E1H1, D2E2H2, D3E3H3;
известную проекцию точки К соединяют с одной из одноименных проекций точек D, E, H отрезком прямой линии так, чтобы он пересек одну из сторон одноименной проекции треугольника DEH в некоторой точке F (F2);
проводят линии связи из полученной проекции точки F (F2) до пересечения с проекцией соответствующей стороны треугольника DEH, получают еще две проекции этой точки (F1 и F3);
проводят прямые через построенные проекции этой точки (F1, F3)
исоответствующие проекции вершин треугольника DEH, отмечают на этой прямой недостающие проекции точки К, используя ли-
нии связи.
Соединив последовательно между собой отрезками прямых линий одноименные проекции точек А, В, С и K, E, D, H, получают проекции тре-
угольной пластины ( А1В1С1, А2В2С2, А3В3С3) и проекции четырехуголь-
ной пластины ( D1E1H1K1, D2E2H2K2, D3E3H3K3).
Построение линии пересечения многоугольников сводится к определению двух точек, общих для этих многоугольников, т. е. точек, принадлежащих линии пересечения, соединив которые, и получают линию пересечения. В рассматриваемом примере (рис. 6) такими точками являются точки M и N.
14

15
Рис. 6
Для определения точки N выполняют построение:
сторону ЕН четырехугольника DEHK заключают в плоскость
α(α1 = Е1Н1);
отмечают точки пересечения плоскости α со сторонами АВ и ВС
треугольника АВС (α1 ∩ А1В1 = 11, α1 ∩ В1С1 = 21, 12 А2В2,
22 В2С2);
соединив проекции 12 и 22 отрезками прямой линии, отмечают точку пересечения (N2) этого отрезка с проекцией Е2Н2 и получают фронтальную проекцию N2 точки пересечения стороны ЕН четырехугольника DEHK с плоскостью треугольника АВС.
проводят линию связи из N2 до Е1Н1, получают N1 – горизонтальную проекцию точки пересечения.
Для определения точки М:
сторону АС треугольника АВС заключают в плоскость β (β2 =
=А2С2);
отмечают точки пересечения плоскости β со сторонами DK и KH
четырехугольника DEHK (β2 ∩ D2K2 = 32, β2 ∩ K2H2 = 42, 31 D1K1,
41 K1H1);
проведя прямую 3141 до пересечения с А1С1, получают точку Р1 – горизонтальную проекцию точки пересечения стороны АС треугольника АВС с плоскостью четырехугольника DEHK;
проводя линию связи из Р1 до А2С2, получают Р2 – фронтальную проекцию точки пересечения стороны АС треугольника АВС с плоскостью четырехугольника DEHK.
Примечание. Сторона АС пересекает плоскость четырехугольника за его пределами. Точку Р можно использовать для определения реального участка линии пересечения. Для этого достаточно, соединив Р1 с N1, отметить точку (М1) пересечения D1K1 и P1N1 и P2 с N2, отметить точку (М2) пересечения P2N2 с D2K2. Причем M1 и M2 должны оказаться на одной линии связи. M1N1 – горизонтальная, M2N2 – фронтальная проекции реального участка линии пересечения заданных многоугольников.
Для определения профильной проекции M3N3 проводят до соответствующих сторон через M2N2 линии связи, перпендикулярные оси OZ:
определяя видимость сторон многоугольников на π1, пользуются конкурирующими точками 2 и 5, 21 51, 22 В2С2, 52 E2H2. Координата z точки 2 больше (22 от оси OX удалена дальше, чем 52), следовательно, точка 2 выше точки 5, а это значит, что сторона ВС, которой принадлежит точка 2, выше стороны ЕН. Поэтому участок N151 – невидимый, N1E1 – видимый, но тогда участок А1В1 – невидимый в пределах проекции D1E1H1K1;
16
для определения видимости на π2 пользуются конкурирующими
точками 4 и 6; 42 62, 41 K1H1, 61 A1C1. Координата y точки 4 больше, чем точки 6 (41 расположена дальше от оси OX, чем точка
61), следовательно, точка 4 видима при проецировании на π2. А это значит, что KH впереди АС. Поэтому K2H2 – видима, а участки
сторон B2C2 и А2С2 – невидимы в пределах проекции D2E2H2K2. Участки N2H2 и M2K2 – видимы полностью, а E2N2 и D2M2 – види-
мы за пределами А2В2С2;
видимость на π3 определяют при помощи конкурирующих точек 7 и 8. Координата x точки 8 больше координаты x точки 7, поэтому точка 8 – видима и M3D3 – видимый участок стороны K3D3. Участок
А3В3 в пределах проекции D3E3H3K3 – невидимый; N3E3 – видимый; N3H3, H3M3, K3M3 – невидимые в пределах проекции А3В3С3;
невидимые участки сторон многоугольников обводят штриховой линией (ГОСТ 2.303-68), видимые – основной линией;
длянаглядностивидимыеучасткипроекцийтреугольникаАВСоттеняют.
Варианты заданий 01
Варианты заданий 01 представлены в табл. 2.
Таблица 2
Номер |
Точка |
Координаты |
Номер |
Точка |
Координаты |
Номер |
Точка |
Координаты |
||||||
варианта |
x |
y |
z |
варианта |
x |
y |
z |
варианта |
x |
y |
z |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
А |
47 |
52 |
55 |
2 |
А |
49 |
55 |
54 |
3 |
А |
100 |
40 |
53 |
|
B |
115 |
67 |
40 |
|
B |
110 |
38 |
65 |
|
B |
20 |
47 |
43 |
|
C |
70 |
0 |
4 |
|
C |
70 |
5 |
0 |
|
C |
40 |
8 |
0 |
|
K |
60 |
68 |
0 |
|
K |
110 |
73 |
5 |
|
K |
42 |
52 |
25 |
|
E |
20 |
40 |
– |
|
E |
23 |
25 |
– |
|
E |
20 |
25 |
– |
|
D |
106 |
4 |
75 |
|
D |
60 |
0 |
65 |
|
D |
120 |
0 |
0 |
|
H |
106 |
30 |
48 |
|
H |
87 |
30 |
53 |
|
H |
77 |
45 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
A |
83 |
60 |
57 |
5 |
A |
95 |
33 |
15 |
6 |
A |
97 |
23 |
50 |
|
B |
17 |
40 |
30 |
|
B |
55 |
70 |
63 |
|
B |
30 |
23 |
50 |
|
C |
110 |
5 |
5 |
|
C |
25 |
5 |
24 |
|
C |
85 |
60 |
15 |
|
K |
42 |
55 |
60 |
|
K |
15 |
20 |
47 |
|
K |
40 |
60 |
60 |
|
E |
95 |
75 |
– |
|
E |
65 |
5 |
– |
|
E |
85 |
60 |
– |
|
D |
110 |
25 |
5 |
|
D |
105 |
18 |
63 |
|
D |
105 |
34 |
8 |
|
H |
22 |
10 |
8 |
|
H |
84 |
63 |
0 |
|
H |
30 |
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
Продолжение табл. 2
Номер |
Точка |
Координаты |
Номер |
Точка |
|
Координаты |
Номер |
Точка |
Координаты |
||||||||
варианта |
x |
y |
z |
варианта |
|
x |
|
y |
z |
варианта |
x |
y |
z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
A |
85 |
53 |
55 |
8 |
A |
97 |
0 |
60 |
9 |
A |
100 |
|
10 |
25 |
||
|
B |
20 |
65 |
40 |
|
B |
32 |
60 |
15 |
|
B |
80 |
|
65 |
57 |
||
|
C |
62 |
0 |
7 |
|
C |
70 |
65 |
0 |
|
C |
40 |
|
24 |
10 |
||
|
K |
70 |
67 |
0 |
|
K |
80 |
60 |
65 |
|
K |
93 |
|
60 |
0 |
||
|
E |
25 |
5 |
75 |
|
E |
42 |
10 |
27 |
|
E |
30 |
|
13 |
108 |
||
|
D |
110 |
40 |
25 |
|
D |
102 |
25 |
10 |
|
E |
70 |
|
0 |
65 |
||
|
H |
10 |
– |
65 |
|
H |
55 |
|
– |
55 |
|
H |
44 |
|
– |
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
A |
98 |
5 |
32 |
11 |
A |
17 |
45 |
105 |
12 |
A |
105 |
|
30 |
55 |
||
|
B |
14 |
5 |
85 |
|
B |
150 |
140 |
70 |
|
B |
35 |
|
60 |
60 |
||
|
C |
70 |
45 |
8 |
|
C |
75 |
0 |
0 |
|
C |
55 |
|
10 |
0 |
||
|
K |
18 |
55 |
5 |
|
K |
120 |
20 |
7 |
|
K |
85 |
|
10 |
48 |
||
|
E |
60 |
12 |
65 |
|
E |
25 |
18 |
50 |
|
E |
105 |
|
70 |
0 |
||
|
D |
123 |
13 |
20 |
|
D |
130 |
50 |
– |
|
D |
40 |
|
60 |
13 |
||
|
H |
98 |
– |
0 |
|
H |
70 |
115 |
120 |
|
H |
25 |
|
– |
40 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
A |
100 |
60 |
60 |
14 |
A |
105 |
15 |
33 |
15 |
A |
105 |
|
45 |
63 |
||
|
B |
15 |
55 |
27 |
|
B |
33 |
60 |
50 |
|
B |
20 |
|
30 |
50 |
||
|
C |
85 |
0 |
0 |
|
C |
52 |
3 |
0 |
|
C |
58 |
|
5 |
12 |
||
|
K |
12 |
23 |
53 |
|
K |
95 |
50 |
22 |
|
K |
27 |
|
68 |
40 |
||
|
E |
78 |
53 |
35 |
|
E |
30 |
50 |
22 |
|
E |
65 |
|
0 |
80 |
||
|
D |
110 |
35 |
0 |
|
D |
85 |
8 |
60 |
|
D |
100 |
|
20 |
8 |
||
|
H |
45 |
0 |
– |
|
H |
20 |
8 |
– |
|
H |
105 |
|
0 |
– |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
A |
115 |
7 |
28 |
17 |
A |
|
113 |
|
5 |
53 |
18 |
A |
108 |
|
22 |
47 |
|
B |
85 |
70 |
65 |
|
B |
|
10 |
|
30 |
15 |
|
B |
18 |
|
22 |
45 |
|
C |
42 |
23 |
10 |
|
C |
|
70 |
|
65 |
10 |
|
C |
90 |
|
63 |
12 |
|
K |
30 |
45 |
25 |
|
K |
|
25 |
|
8 |
20 |
|
K |
20 |
|
45 |
25 |
|
E |
90 |
25 |
40 |
|
E |
|
76 |
|
8 |
55 |
|
E |
32 |
|
0 |
50 |
|
D |
98 |
60 |
0 |
|
D |
|
115 |
65 |
27 |
|
D |
113 |
|
55 |
27 |
|
|
H |
30 |
15 |
– |
|
H |
|
80 |
|
72 |
– |
|
H |
78 |
|
75 |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
A |
105 |
30 |
15 |
20 |
A |
|
120 |
|
0 |
60 |
21 |
A |
120 |
|
100 |
65 |
|
B |
35 |
60 |
60 |
|
B |
|
35 |
|
15 |
30 |
|
B |
35 |
|
45 |
40 |
|
C |
50 |
0 |
5 |
|
C |
|
70 |
|
60 |
0 |
|
C |
90 |
|
10 |
0 |
|
K |
60 |
65 |
55 |
|
K |
|
45 |
|
5 |
10 |
|
K |
45 |
|
70 |
60 |
|
E |
95 |
10 |
5 |
|
E |
|
95 |
|
50 |
60 |
|
E |
85 |
|
80 |
65 |
|
D |
95 |
60 |
50 |
|
D |
|
130 |
25 |
25 |
|
D |
140 |
|
55 |
25 |
|
|
H |
10 |
40 |
– |
|
H |
|
45 |
|
40 |
– |
|
H |
60 |
|
– |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Окончание табл. 2
Номер |
Точка |
Координаты |
Номер |
Точка |
|
Координаты |
Номер |
Точка |
Координаты |
|||||||||
варианта |
x |
y |
z |
варианта |
|
x |
|
y |
z |
варианта |
x |
y |
z |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
A |
135 |
95 |
|
70 |
23 |
A |
|
130 |
|
70 |
25 |
24 |
A |
105 |
|
50 |
75 |
|
B |
50 |
40 |
|
35 |
|
B |
|
40 |
|
70 |
85 |
|
B |
70 |
|
10 |
0 |
|
C |
125 |
15 |
|
5 |
|
C |
|
60 |
|
0 |
0 |
|
C |
10 |
|
80 |
60 |
|
|
|
|
|
|
|||||||||||||
|
K |
60 |
60 |
|
65 |
|
K |
|
105 |
15 |
10 |
|
K |
5 |
|
55 |
45 |
|
|
E |
150 |
60 |
|
25 |
|
E |
|
15 |
|
80 |
55 |
|
E |
75 |
|
85 |
85 |
|
D |
110 |
85 |
|
65 |
|
D |
|
120 |
75 |
80 |
|
D |
115 |
|
20 |
20 |
|
|
H |
90 |
– |
|
5 |
|
H |
|
40 |
|
– |
10 |
|
H |
30 |
|
20 |
– |
25 |
A |
140 |
35 |
|
10 |
26 |
A |
|
40 |
|
80 |
35 |
27 |
A |
140 |
|
40 |
65 |
|
B |
105 |
90 |
|
75 |
|
B |
|
75 |
|
0 |
0 |
|
B |
45 |
|
30 |
75 |
|
C |
35 |
10 |
|
10 |
|
C |
|
115 |
20 |
70 |
|
C |
110 |
|
85 |
10 |
|
|
K |
23 |
55 |
|
– |
|
K |
|
110 |
65 |
85 |
|
K |
50 |
|
10 |
20 |
|
|
E |
80 |
85 |
|
65 |
|
E |
|
80 |
|
10 |
10 |
|
E |
90 |
|
85 |
85 |
|
D |
125 |
10 |
|
0 |
|
D |
|
25 |
|
20 |
20 |
|
D |
150 |
|
25 |
40 |
|
H |
65 |
10 |
|
0 |
|
H |
|
45 |
|
55 |
– |
|
H |
125 |
|
– |
20 |
28 |
A |
115 |
60 |
|
0 |
29 |
A |
|
130 |
60 |
70 |
30 |
A |
105 |
|
85 |
10 |
|
|
B |
95 |
0 |
|
85 |
|
B |
|
5 |
|
30 |
75 |
|
B |
50 |
|
25 |
80 |
|
C |
25 |
0 |
|
0 |
|
C |
|
65 |
|
5 |
5 |
|
C |
0 |
|
80 |
50 |
|
K |
40 |
30 |
|
55 |
|
K |
|
35 |
|
25 |
55 |
|
K |
20 |
|
50 |
0 |
|
E |
135 |
10 |
|
0 |
|
E |
|
100 |
45 |
25 |
|
E |
85 |
|
35 |
25 |
|
|
D |
80 |
60 |
|
80 |
|
D |
|
110 |
0 |
65 |
|
D |
65 |
|
90 |
85 |
|
|
H |
60 |
10 |
|
– |
|
H |
|
35 |
|
– |
10 |
|
H |
105 |
|
– |
60 |
Расчетно-графическое задание 02
МНОГОГРАННИКИ. МЕТРИЧЕСКИЕ И ПОЗИЦИОННЫЕ ЗАДАЧИ
Цель – закрепить знания и умения по следующим темам: «Сечение многогранника плоскостью общего положения», «Способы преобразования ортогональных проекций – замена плоскостей проекций».
Расчетно-графическое задание 02 выполняют на двух листах: первый лист – решение задачи 02.01 (формат А3) (рис. 10), второй лист – решение задач 02.02 (формат А4) (рис. 11).
Содержание работы
Задача 02.01. По данным координатам вершин (табл. 3) построить многогранник и задать плоскость общего положения. Определить фигуру сечения многогранника этой плоскостью.
19
Задача 02.02. Определить натуральный вид сечения, применяя для этого способ замены плоскостей проекций.
Методические рекомендации к выполнению задачи 02.01
Многогранником называется тело, ограниченное плоскими многоугольниками. Многогранник, две грани которого конгруэнтны, а остальные пересекаются по параллельным прямым, называется призмой. Название призмы зависит от того, какой многоугольник лежит в ее основании, если треугольник, то и призма называется треугольной, если четырехугольник, то призма будет четырехугольной и т. д.
Многогранник, одна грань которого (основание) есть многоугольник, а остальные грани – треугольники с общей вершиной, называется пирамидой.
Пирамиды и призмы могут быть правильными, если их основанием служит правильный многоугольник и высота проходит через его центр.
Сечением называется плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.
Сечением многогранника плоскостью является многоугольник, вершинами которого служат точки пересечения ребер многогранника с секущей плоскостью, а сторонами – линии пересечения граней с секущей плоскостью (рис. 7).
Рис. 7
20
Поэтому построение сечения многогранника плоскостью предполагает деление точек пересечения ребер многогранника с заданной секущей плоскостью и соединение между собой этих точек, принадлежащих одной и той же грани отрезками прямых линий.
Задача, таким образом, сводится к многократному решению основной позиционной задачи – пересечение прямой с плоскостью.
Внекоторых случаях данная секущая плоскость пересекает основание многогранника. Тогда некоторые боковые ребра многогранника имеют точки встречи с секущей плоскостью на своем продолжении и могут находиться за пределами чертежа. В этом случае удобно воспользоваться тем, что плоскость основания проецирующая, поэтому можно определить линию пересечения ее с секущей плоскостью. Эта линия пересекает стороны основания в точках, являющихся вершинами сечения.
Вкачестве примера решения задачи 02.01 рассмотрено построение
сечения четырехугольной призмы ABCDA B C D плоскостью ( KLM) (рис. 10).
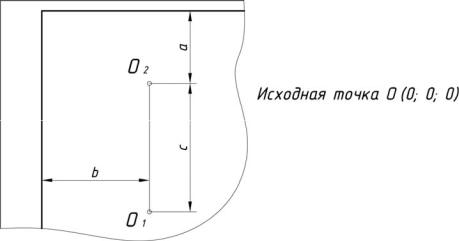
Выполнение работы следует начинать с выделения на формате поля чертежа, т. е. с нанесения рамки и основной надписи. Затем построить проекции точки, имеющей нулевые координаты. Положение проекций этой точки заданы указанными расстояниями их от сторон рамки чертежа. Например, точка A(0; 0; 0) имеет нулевые координаты (рис. 8). Чтобы построить ее проекцию A2, нужно от левой стороны рамки чертежа отступить вправо на 210 мм, а от верхней вниз – на 150 мм. Через A2 провести вертикальную линию связи и отложив на ней отрезок длиной 120 мм, получить горизонтальную проекцию A1.
Проекции остальных вершин многогранника и точек, определяющих секущую плоскость, находят, считая проекции нулевой точки за точки отсчета. Например, чтобы построить горизонтальную проекцию точки B(40; 15; 10) (B1) (рис. 9) нужно от горизонтальной проекции нулевой точки A1 отступить влево на 40 мм (x = 40) и вниз – на 15 мм (y = 15). Для получения фронтальной проекции точки B (B2) отступают влево на 40 мм (x = 40), вверх – на 10 мм (z = 10) от фронтальной проекции нулевой точки A2.
Построив таким способом проекции всех точек, данных в условии задачи, соединяют одноименные проекции точек отрезками прямых так, чтобы получились проекции указанного многогранника (призмы или пирамиды) и секущей плоскости.
Причем для призмы даны координаты всех вершин одного основания и координаты одной вершины второго основания. Проекции вершин, координаты которых не даны, находят с учетом того, что боковые ребра призмы параллельны и равны между собой по длине. Следовательно, одноименные проекции боковых ребер также равны и параллельны между собой.
21

Рис. 8 |
Рис. 9 |
Последовательность построений
1. Определяют проекции точки пересечения ребра AA с секущей плоскостью ( KLM). Для этого:
в секущей плоскости ( KLM) проводят прямую, конкурирую-
щую с ребром AA , т. е. 1222 = A2A2 , причем 12 = A2A2 K2M2,
22 = A2A2 L2M2;
через 12 и 22 проводят вертикальные линии связи соответственно до K1M1 и L1M1 и получают проекции 11 и 21;
соединяют 11 и 21 и отмечают точку пересечения прямой 1121 с
A1A1 (1121 A1A1 = N1);
через N1 проводят линию связи до пересечения с A2A2 в точке N2. N1 и N2 – проекции точки пересечения ребра AA с секущей плоскостью ( KLM).
2. Аналогично определяют проекции точек пересечения ребер BB ,
CC и DD секущей плоскостью ( KLM): R (R1,R2), S (S1,S2) и P (P1,P2). Одноименные проекции точек пересечения ребер с секущей плоскостью ,
принадлежащих одной грани, соединяют отрезками прямых, учитывая их видимость (невидимые обводят штриховой линией).
Многоугольник N1S1P1R1 – горизонтальная проекция сечения. Многоугольник N2S2P2R2 – фронтальная проекция сечения.
22
Методические рекомендации к выполнению задачи 02.02
Для определения формы и действительных размеров плоской фигуры воспользуемся одним из способов преобразования ортогональных проекций – заменой плоскостей проекций.
По сути нам необходимо преобразовать чертеж так, чтобы плоскость фигуры стала плоскостью уровня. Первая замена плоскости преобразует плоскость общего положения в плоскость проецирующую. Новая плоскость должна быть перпендикулярна одной из линий уровня этой плоскости, например, фронтали.
Последовательность построений
1. Проекции сечения N1S1P1R1 и N2S2P2R2 выносят на новый формат А4 (рис. 11).
2. В плоскости (NSPR) проводят f = S1 (f1 проводят через S1 параллельно оси x1,2, отмечают точку пересечения 11 прямых R1P1 и f1; проведя линию связи из точки 11 до пересечения ее с R2P2, отмечают 12; S212 = f2 ).
3.Перпендикулярно f2 (S212) проводят новую ось проекций x2,4.
4.Перпендикулярно новой оси проекций x2,4 проводят линии связи через проекции S2, P2, N2, R2 и откладывают на них координаты y этих то-
чек, измеряя расстояние от оси проекций x1,2 до проекций N1, S1, P1, R1.
5.Прямая, проходящая через проекции S4, P4, N4, R4 ( 4), является проекцией плоскости ( S, P, N, R) на плоскость 4.
6.Проецирующую плоскость 4 преобразуют в плоскость уровня. Для этого новую плоскость проекций 4 проводят параллельно плоскости, а именно:
новую ось проекций x4,5 проводят параллельно проекции плоско-
сти 4;
из точек S4, P4, N4, R4 проводят линии связи перпендикулярно новой оси x4,5, откладывают на них отрезки, равные расстоянию от
проекций S2, P2, N2, R2 до оси x2,4, и получают точки S5, P5, N5, R5;соединив полученные точки отрезками, получают четырехуголь-
ник, который является истинной величиной.
23
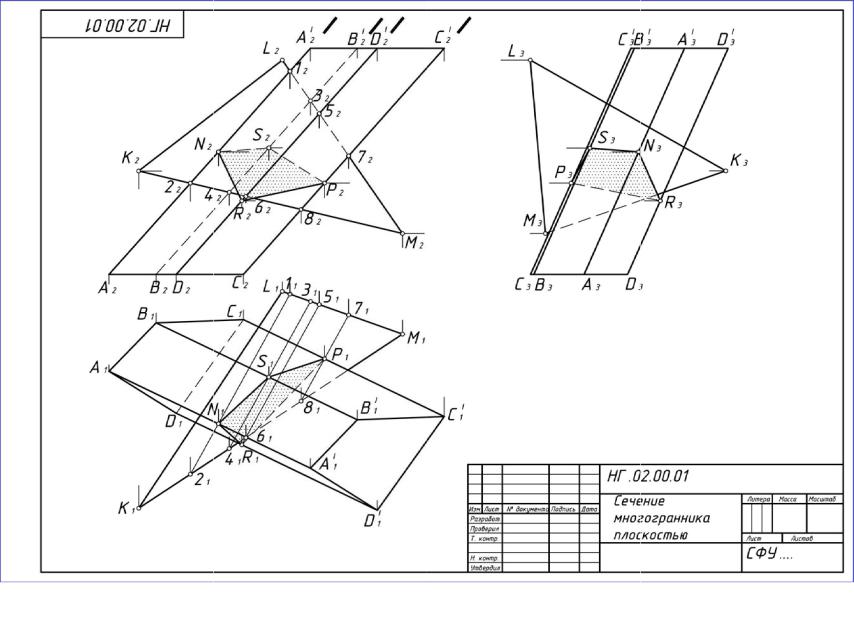
24
Рис. 10
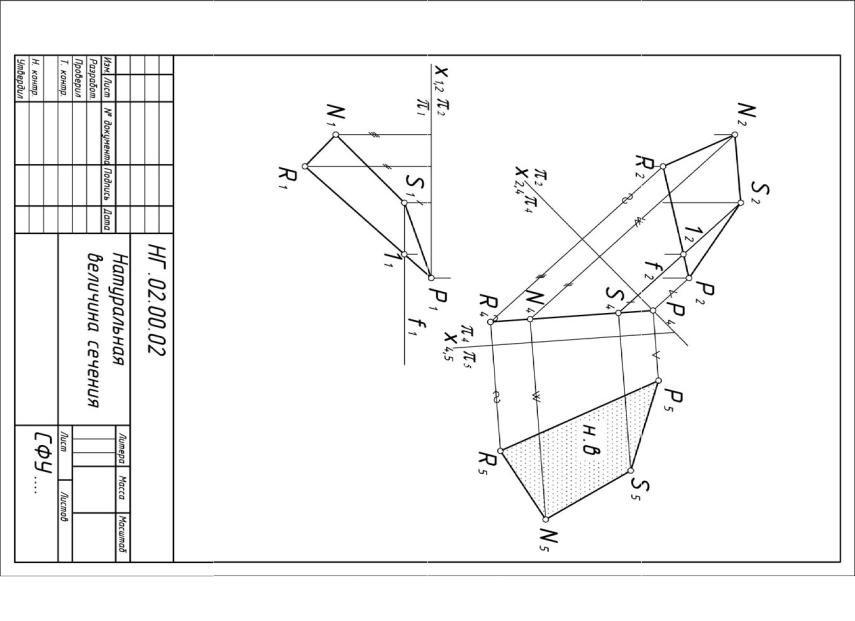
25
Рис. 11
Варианты заданий 02
Варианты заданий 02 представлены в табл. 3.
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ис- |
|
|
|
Вер- |
|
|
|
Плос- |
|
|
|
|
|
Номер |
ход- |
|
|
|
шина |
|
|
|
|
|
|
|
|
|
a |
b |
c |
x |
y |
z |
кость |
x |
y |
|
z |
|||
|
вариан- |
ная |
много- |
|
||||||||||
|
та |
точ- |
|
|
|
гран- |
|
|
|
∑ |
|
|
|
|
|
|
ка |
|
|
|
ника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
В |
150 |
205 |
70 |
Призма ABCDA B C D |
|
(M, K, L) |
|
|||||
|
|
|
|
|
|
A |
40 |
0 |
25 |
М |
120 |
6 |
|
5 |
|
|
|
|
|
|
C |
65 |
0 |
10 |
K |
10 |
15 |
|
70 |
|
|
|
|
|
|
D |
80 |
0 |
25 |
L |
–25 |
80 |
|
25 |
|
|
|
|
|
|
B |
80 |
60 |
40 |
|
|
|
|
|
|
2 |
В |
150 |
150 |
100 |
|
Пирамида SBCED |
|
(A, |
M, N) |
|
|
||
|
C |
25 |
–60 |
0 |
М |
–52 |
50 |
|
15 |
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
D |
50 |
30 |
0 |
N |
75 |
–50 |
|
15 |
|
|
|
|
|
|
E |
92 |
–20 |
0 |
A |
92 |
–15 |
|
110 |
|
|
|
|
|
|
S |
–55 |
45 |
110 |
|
|
|
|
|
|
3 |
E |
175 |
125 |
75 |
Призма ABDEA B D E |
|
(K, L, N) |
|
|||||
|
|
|
|
|
|
E |
–78 |
55 |
100 |
K |
85 |
20 |
|
20 |
|
|
|
|
|
|
D |
17 |
–20 |
0 |
L |
–60 |
–18 |
|
65 |
|
|
|
|
|
|
B |
63 |
–25 |
0 |
N |
–90 |
20 |
|
15 |
|
|
|
|
|
|
A |
80 |
3 |
0 |
|
|
|
|
|
|
4 |
A |
180 |
175 |
120 |
Пирамида SABDEC |
|
(MN ∩ NK) |
|
|||||
|
|
|
|
|
|
S |
145 |
–20 |
130 |
M |
145 |
–10 |
|
40 |
|
|
|
|
|
|
B |
5 |
–35 |
0 |
N |
55 |
–60 |
|
75 |
|
|
|
|
|
|
C |
45 |
40 |
0 |
K |
–10 |
10 |
|
5 |
|
|
|
|
|
|
D |
70 |
–45 |
0 |
|
|
|
|
|
|
|
|
|
|
|
E |
90 |
30 |
0 |
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Продолжение табл. 3
Но- |
Ис- |
|
|
|
Вер |
|
|
|
|
|
|
|
|
|
|
|
шина |
|
|
|
Плос- |
|
|
|
|||
мер |
ход- |
|
|
|
|
|
|
|
|
|
|||
a |
b |
c |
мно- |
x |
y |
|
кость |
x |
y |
z |
|||
ва- |
ная |
z |
|||||||||||
ри- |
точ- |
|
|
|
го- |
|
|
∑ |
|
|
|
||
|
|
|
гран- |
|
|
|
|
|
|
||||
анта |
ка |
|
|
|
|
|
|
|
|
|
|||
|
|
|
ника |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
S |
185 |
195 |
145 |
Пирамида SABCD |
|
(M, N, L) |
|
|||||
|
|
|
|
|
A |
130 |
–145 |
70 |
М |
140 |
–110 |
85 |
|
|
|
|
|
|
B |
45 |
–145 |
100 |
N |
80 |
15 |
115 |
|
|
|
|
|
|
C |
33 |
–145 |
35 |
L |
–20 |
–65 |
35 |
|
|
|
|
|
|
D |
85 |
–145 |
20 |
|
|
|
|
|
6 |
L |
75 |
145 |
140 |
Пирамида SKLNM |
|
(AB ∩ AC) |
|
|||||
|
|
|
|
|
S |
105 |
100 |
–90 |
A |
113 |
36 |
–33 |
|
|
|
|
|
|
M |
60 |
0 |
–33 |
B |
20 |
85 |
34 |
|
|
|
|
|
|
N |
73 |
0 |
30 |
C |
–30 |
20 |
6 |
|
|
|
|
|
|
K |
22 |
0 |
–51 |
|
|
|
|
|
7 |
D |
120 |
195 |
110 |
Пирамида SABCD |
|
(F, GE) |
|
|||||
|
|
|
|
|
S |
150 |
–65 |
115 |
G |
140 |
–85 |
25 |
|
|
|
|
|
|
A |
110 |
10 |
0 |
E |
50 |
–85 |
60 |
|
|
|
|
|
|
B |
70 |
40 |
0 |
F |
30 |
50 |
45 |
|
|
|
|
|
|
C |
35 |
–45 |
0 |
|
|
|
|
|
8 |
D |
100 |
145 |
160 |
Пирамида SABCDE |
|
(∆MKL) |
|
|||||
|
|
|
|
|
S |
–55 |
–110 |
110 |
L |
–45 |
–50 |
16 |
|
|
|
|
|
|
C |
15 |
–25 |
0 |
M |
90 |
–45 |
50 |
|
|
|
|
|
|
E |
30 |
20 |
0 |
K |
–70 |
25 |
75 |
|
|
|
|
|
|
B |
60 |
–30 |
0 |
|
|
|
|
|
|
|
|
|
|
A |
90 |
5 |
0 |
|
|
|
|
|
9 |
В |
150 |
205 |
70 |
Призма ABCDA B C D |
|
(M, K, L) |
|
|||||
|
|
|
|
|
A |
40 |
0 |
25 |
М |
120 |
6 |
5 |
|
|
|
|
|
|
C |
65 |
0 |
10 |
K |
10 |
15 |
70 |
|
|
|
|
|
|
D |
80 |
0 |
25 |
L |
–25 |
80 |
25 |
|
|
|
|
|
|
B |
80 |
60 |
40 |
|
|
|
|
|
10 |
D |
120 |
200 |
90 |
Пирамида SABCDE |
|
(M, K, L) |
|
|||||
|
|
|
|
|
S |
156 |
130 |
65 |
K |
–16 |
30 |
31 |
|
|
|
|
|
|
A |
77 |
0 |
–38 |
L |
163 |
40 |
–3 |
|
|
|
|
|
|
B |
65 |
0 |
13 |
M |
0 |
82 |
–41 |
|
|
|
|
|
|
C |
27 |
0 |
37 |
|
|
|
|
|
|
|
|
|
|
E |
38 |
0 |
–57 |
|
|
|
|
|
11 |
C |
150 |
190 |
70 |
Призма ABCDA B C D |
|
(MN, K) |
|
|||||
A |
95 |
0 |
6 |
K |
165 |
0 |
–5 |
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
B |
20 |
0 |
45 |
M |
25 |
50 |
145 |
|
|
|
|
|
|
D |
45 |
0 |
–15 |
N |
25 |
120 |
80 |
|
|
|
|
|
|
A |
165 |
110 |
100 |
|
|
|
|
|
27

Продолжение табл. 3
|
|
|
|
|
Вер- |
|
|
z |
|
|
|
|
|
Но- |
Ис- |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
шина |
|
|
|
Плос- |
|
|
|
|||
мер |
ход- |
|
|
|
|
|
|
|
|
|
|||
a |
b |
c |
мно- |
x |
y |
|
кость |
x |
y |
z |
|||
вари- |
ная |
|
|||||||||||
анта |
точ- |
|
|
|
го- |
|
|
|
∑ |
|
|
|
|
|
|
|
гран- |
|
|
|
|
|
|
||||
|
ка |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ника |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
D |
150 |
115 |
110 |
Призма ABCDA B C D |
|
(MK ∩ KN) |
|
|||||
A |
|
60 |
–6 |
0 |
K |
–50 |
–85 |
30 |
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
B |
|
40 |
–20 |
0 |
M |
30 |
–75 |
95 |
|
|
|
|
|
C |
|
30 |
40 |
0 |
N |
–5 |
–8 |
20 |
|
|
|
|
|
D |
|
–70 |
–55 |
90 |
|
|
|
|
13 |
L |
145 |
185 |
70 |
Пирамида SMNLK |
|
(∆ABC) |
|
|||||
|
|
|
|
|
K |
|
80 |
0 |
–30 |
A |
140 |
40 |
110 |
|
|
|
|
|
M |
|
95 |
0 |
40 |
B |
–10 |
70 |
120 |
|
|
|
|
|
N |
|
35 |
0 |
70 |
C |
10 |
30 |
–30 |
|
|
|
|
|
S |
|
150 |
120 |
100 |
|
|
|
|
14 |
C |
195 |
210 |
45 |
Призма ABCDA B C D |
|
(∆LMN) |
|
|||||
|
|
|
|
|
A |
|
90 |
35 |
0 |
L |
195 |
0 |
80 |
|
|
|
|
|
B |
|
65 |
–10 |
0 |
M |
55 |
–30 |
140 |
|
|
|
|
|
D |
|
30 |
70 |
0 |
N |
15 |
90 |
40 |
|
|
|
|
|
A |
|
185 |
95 |
120 |
|
|
|
|
15 |
C |
60 |
200 |
285 |
Призма ABCDA B C D |
|
(MK ∩ KN) |
|
|||||
|
|
|
|
|
A |
|
87 |
–6 |
0 |
M |
170 |
–50 |
34 |
|
|
|
|
|
B |
|
97 |
15 |
0 |
K |
21 |
–67 |
–74 |
|
|
|
|
|
D |
|
40 |
–24 |
0 |
N |
137 |
5 |
–24 |
|
|
|
|
|
C |
|
70 |
–120 |
–130 |
|
|
|
|
16 |
C |
195 |
195 |
80 |
|
|
Пирамида SABCD |
|
(E, |
F, K) |
|
||
|
|
|
|
|
A |
|
110 |
–50 |
0 |
E |
160 |
–40 |
30 |
|
|
|
|
|
B |
|
60 |
–45 |
0 |
F |
70 |
90 |
140 |
|
|
|
|
|
D |
|
30 |
50 |
0 |
K |
0 |
50 |
40 |
|
|
|
|
|
S |
|
170 |
60 |
140 |
|
|
|
|
17 |
C |
75 |
180 |
140 |
Призма ABCDA B C D |
|
(MN, L) |
|
|||||
A |
|
82 |
0 |
20 |
L |
152 |
20 |
0 |
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
B |
|
36 |
0 |
26 |
M |
–10 |
20 |
0 |
|
|
|
|
|
D |
|
64 |
0 |
–30 |
N |
–10 |
100 |
60 |
|
|
|
|
|
A |
|
156 |
100 |
–60 |
|
|
|
|
18 |
S |
35 |
195 |
160 |
|
|
Пирамида SABCD |
|
(MN |
KL) |
|
||
|
|
|
|
|
A |
|
160 |
90 |
–130 |
M |
100 |
–20 |
–10 |
|
|
|
|
|
B |
|
120 |
50 |
–130 |
N |
–20 |
90 |
–70 |
|
|
|
|
|
C |
|
50 |
115 |
–130 |
K |
100 |
30 |
–70 |
|
|
|
|
|
D |
|
120 |
130 |
–130 |
L |
–20 |
140 |
–130 |
28
Продолжение табл. 3
|
Ис- |
|
|
|
Вер- |
|
|
|
|
|
|
|
|
Но- |
|
|
|
шина |
|
|
|
Плос- |
|
|
|
||
ход- |
|
|
|
|
|
|
|
|
|
||||
мер |
ная |
a |
b |
c |
мно- |
x |
y |
z |
кость |
x |
y |
z |
|
вари- |
точ- |
|
|
|
го- |
|
|
|
∑ |
|
|
|
|
анта |
ка |
|
|
|
гран- |
|
|
|
|
|
|
||
|
|
|
|
|
ника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
C |
195 |
195 |
40 |
|
Пирамида SABCD |
|
(MK ∩ KN) |
|
||||
|
|
|
|
|
A |
|
110 |
–20 |
140 |
M |
160 |
–40 |
30 |
|
|
|
|
|
B |
|
60 |
–35 |
0 |
N |
0 |
50 |
40 |
|
|
|
|
|
D |
|
30 |
0 |
0 |
K |
70 |
90 |
100 |
|
|
|
|
|
S |
|
170 |
60 |
140 |
|
|
|
|
20 |
D |
145 |
180 |
180 |
Пирамида SABCDE |
|
(∆MKL) |
|
|||||
|
|
|
|
|
S |
|
140 |
–100 |
100 |
K |
140 |
–40 |
60 |
|
|
|
|
|
A |
|
90 |
10 |
0 |
L |
80 |
40 |
10 |
|
|
|
|
|
B |
|
70 |
–30 |
0 |
M |
–20 |
–80 |
50 |
|
|
|
|
|
C |
|
20 |
–40 |
0 |
|
|
|
|
|
|
|
|
|
E |
|
50 |
40 |
0 |
|
|
|
|
21 |
S |
160 |
175 |
120 |
|
Пирамида SABCD |
|
(M, K, N) |
|
||||
|
|
|
|
|
A |
|
130 |
–100 |
80 |
M |
50 |
–35 |
0 |
|
|
|
|
|
B |
|
80 |
–100 |
110 |
N |
–30 |
–115 |
85 |
|
|
|
|
|
C |
|
25 |
–100 |
80 |
K |
110 |
–60 |
120 |
|
|
|
|
|
D |
|
110 |
–100 |
40 |
|
|
|
|
22 |
S |
80 |
190 |
285 |
|
Пирамида SABCD |
|
(M, K, N) |
|
||||
|
|
|
|
|
A |
|
150 |
–110 |
–120 |
M |
171 |
–62 |
–20 |
|
|
|
|
|
B |
|
112 |
–137 |
–120 |
N |
135 |
–128 |
70 |
|
|
|
|
|
C |
|
56 |
–123 |
–120 |
K |
–10 |
–73 |
–67 |
|
|
|
|
|
D |
|
126 |
–62 |
–120 |
|
|
|
|
23 |
S |
180 |
180 |
155 |
Пирамида SABCDE |
|
(M, K, N) |
|
|||||
|
|
|
|
|
A |
|
140 |
–100 |
100 |
K |
0 |
–40 |
60 |
|
|
|
|
|
B |
|
85 |
–100 |
135 |
N |
40 |
–110 |
105 |
|
|
|
|
|
C |
|
50 |
–100 |
110 |
M |
160 |
–55 |
20 |
|
|
|
|
|
D |
|
70 |
–100 |
70 |
|
|
|
|
|
|
|
|
|
E |
|
120 |
–100 |
60 |
|
|
|
|
24 |
C |
155 |
225 |
40 |
Призма ABCDA B C D |
|
(K, M, L) |
|
|||||
|
|
|
|
|
A |
|
60 |
0 |
–10 |
L |
170 |
15 |
0 |
|
|
|
|
|
B |
|
40 |
0 |
35 |
M |
30 |
15 |
10 |
|
|
|
|
|
D |
|
30 |
0 |
–30 |
K |
–10 |
75 |
100 |
|
|
|
|
|
A |
172 |
125 |
85 |
|
|
|
|
|
25 |
C |
175 |
190 |
80 |
|
Пирамида SABCD |
|
(MN ∩ NL) |
|
||||
|
|
|
|
|
A |
|
80 |
–25 |
0 |
M |
125 |
–18 |
8 |
|
|
|
|
|
B |
|
28 |
–35 |
0 |
N |
95 |
20 |
0 |
|
|
|
|
|
D |
|
55 |
40 |
0 |
L |
–6 |
–50 |
50 |
|
|
|
|
|
S |
|
155 |
40 |
105 |
|
|
|
|
29
Окончание табл. 3
|
Ис- |
|
|
|
Вер- |
|
|
|
|
|
|
|
Но- |
|
|
|
шина |
|
|
|
Плос- |
|
|
|
|
ход- |
|
|
|
|
|
|
|
|
|
|||
мер |
ная |
a |
b |
c |
мно- |
x |
y |
z |
кость |
x |
y |
z |
вари- |
точ- |
|
|
|
го- |
|
|
|
∑ |
|
|
|
анта |
ка |
|
|
|
гран- |
|
|
|
|
|
|
|
|
|
|
|
|
ника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
C |
190 |
190 |
60 |
Пирамида SABCD |
|
(MN ∩ NL) |
|
||||
|
|
|
|
|
A |
92 |
–10 |
0 |
M |
122 |
0 |
18 |
|
|
|
|
|
B |
37 |
–22 |
0 |
N |
50 |
–32 |
110 |
|
|
|
|
|
D |
63 |
56 |
0 |
L |
–13 |
80 |
110 |
|
|
|
|
|
S |
150 |
40 |
140 |
|
|
|
|
27 |
C |
200 |
190 |
60 |
Пирамида SABCD |
|
(M, NL) |
|
||||
|
|
|
|
|
A |
90 |
10 |
0 |
M |
140 |
55 |
45 |
|
|
|
|
|
B |
50 |
–50 |
0 |
N |
0 |
35 |
110 |
|
|
|
|
|
D |
25 |
40 |
0 |
L |
13 |
–35 |
28 |
|
|
|
|
|
S |
150 |
30 |
140 |
|
|
|
|
28 |
D |
90 |
170 |
70 |
Призма ABCDA B C D |
|
(FK ∩ FM) |
|
||||
|
|
|
|
|
A |
28 |
53 |
–37 |
F |
25 |
117 |
83 |
|
|
|
|
|
B |
100 |
51 |
–21 |
M |
148 |
148 |
10 |
|
|
|
|
|
C |
72 |
–4 |
27 |
K |
125 |
17 |
–32 |
|
|
|
|
|
D |
55 |
56 |
48 |
|
|
|
|
29 |
S |
185 |
195 |
145 |
Пирамида SABCD |
|
(M, N, L) |
|
||||
|
|
|
|
|
A |
130 |
–145 |
70 |
M |
140 |
–110 |
85 |
|
|
|
|
|
B |
45 |
–145 |
100 |
N |
80 |
15 |
115 |
|
|
|
|
|
C |
33 |
–145 |
35 |
L |
–20 |
–65 |
35 |
|
|
|
|
|
D |
85 |
–145 |
20 |
|
|
|
|
30 |
D |
100 |
145 |
160 |
Пирамида SABCDE |
|
(∆MKL) |
|
||||
|
|
|
|
|
A |
90 |
5 |
0 |
K |
–70 |
25 |
50 |
|
|
|
|
|
B |
60 |
–30 |
0 |
L |
–45 |
–50 |
16 |
|
|
|
|
|
C |
15 |
–25 |
0 |
M |
90 |
–45 |
50 |
|
|
|
|
|
E |
30 |
20 |
0 |
|
|
|
|
|
|
|
|
|
S |
–55 |
–110 |
110 |
|
|
|
|
30
Расчетно-графическое задание 03
ПОВЕРХНОСТИ. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ. РАЗВЕРТКИ
Цель – закрепить знания по указанной теме.
Содержание задания
Задача 03.01. Построить горизонтальную и фронтальную проекции заданных поверхностей и определить линию их пересечения.
Задача 03.02. Построить развертку одной из поверхностей.
Методические рекомендации к выполнению задачи 03.01
Для успешного выполнения задания необходимо владеть теорией по указанной теме, а именно, знать:
определение поверхности вращения;
общее правило (алгоритм) решения задачи по определению точек, принадлежащих линии пересечения поверхностей;
на каком принципе основан выбор поверхностей-посредников;
определение, свойстваиспособыпостроенияразверткиповерхностей. Задачи на построение линии пересечения поверхностей α и β отно-
сятся к позиционным. Это задачи на определение общих элементов заданных фигур. Линия их пересечения состоит из точек, принадлежащих обеим поверхностям. Общим приемом нахождения этих точек является введение вспомогательных поверхностей-посредников согласно следующему правилу (алгоритму) (рис. 12):
1)ввести вспомогательную поверхность ;
2)построить линии пересечения вспомогательной поверхности с заданными и ( ∩ = а, ∩ = b).
3)отметить точку пересечения построенных линий (K = a ∩ b).
4)повторив эту операцию неоднократно и получив достаточное количество точек, провести через них искомую линию пересечения l (с уче-
том видимости) ∩ = l K, L, M,… .
31
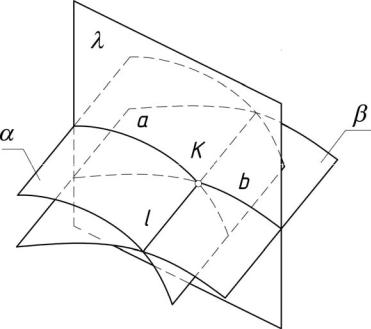
Рис. 12
В качестве вспомогательных поверхностей применяют такие, линии пересечения которых с заданными поверхностями проецируются графически простыми – прямой или окружностью. Можно, например, использовать плоскости или сферы. Если одна из исходных поверхностей линейчатая (образующая – прямая линия), то задача может быть сведена к построению точек пересечения образующих этой поверхности со второй поверхностью. Применяют способы преобразования чертежа, если это упрощает и уточняет решение. Построение точек пересечения рекомендуется выполнять в определенной последовательности: границы видимости, экстремальные и опорные точки, промежуточные (случайные) точки.
Границы видимости – это точки, отделяющие видимую часть линии пересечения от невидимой. Они всегда принадлежат очерковым линиям поверхности.
К экстремальным точкам относятся самая верхняя и самая нижняя точки линии пересечения, самая левая и самая правая, самая ближняя и самая дальняя.
Опорные точки принадлежат границам составных частей поверхности.
Для успешного выполнения задания необходимо свободно владеть пройденным материалом:
уметь выделять на поверхности семейства линий (по возможности простейших: прямых и окружностей);
уметь строить проекции точек и линий на поверхности;
32
знать и применять свойства проекций проецирующих фигур;
знать общий алгоритм определения точек, принадлежащих линии пересечения поверхностей;
знать условия, при которых линия пересечения поверхностей второго порядка распадается на две плоские кривые.
Вкаждом варианте задания предлагается решить две задачи на построение линии пересечения поверхностей.
Две поверхности пересекаются в общем случае по пространственной линии, точки которой принадлежат каждой из заданных поверхностей. Для построения линии пересечения находят ряд точек, общих для обеих поверхностей, и соединяют их линией с учетом ее видимости. Общим приемом нахождения точек, принадлежащих линии пересечения двух поверхностей, является введение вспомогательных поверхностей, в качестве которых рекомендуется чаще всего использовать плоскости и сферы.
Семейство сфер с постоянным центром и переменным радиусом (способ концентрических сфер) применяют при построении линии пересечения поверхностей вращения с пересекающимися осями. Общий центр таких сфер находится в точке пересечения осей данных поверхностей.
Вслучае если оси поверхностей скрещиваются, но одна из поверхностей обязательно является поверхностью вращения, а другая имеет с первой общую плоскость симметрии, параллельную одной из плоскостей проекций, в качестве вспомогательных вводят сферы с переменным центром (способ эксцентрических сфер). Для определения центров вспомогательных сфер на одной из поверхностей задают круговое сечение и отмечают точку пересечения его с осью второй поверхности. Эта точка и будет центром вспомогательной сферы. Круговое сечение может быть принято за параллель вспомогательной сферы. Радиус вспомогательной сферы равен расстоянию от центра ее до крайних точек кругового сечения. Вторую заданную поверхность вспомогательная сфера пересечет также по окружности, т. к. центр вспомогательной сферы оказывается на оси второй поверхности.
Если хотя бы одна из пересекающихся поверхностей занимает проецирующее положение, то решение задачи упрощается, т. к. сразу известна одна из проекций линии пересечения – она совпадает со следом проецирующей поверхности. Вторую проекцию искомой линии определяют из условия ее принадлежности другой, непроецирующей поверхности.
Построение проекций линии пересечения упрощаются и в некоторых частных случаях, которые описываются рядом теорем (например, теоремой Монжа).
Рассмотрим примеры решения некоторых задач.
33
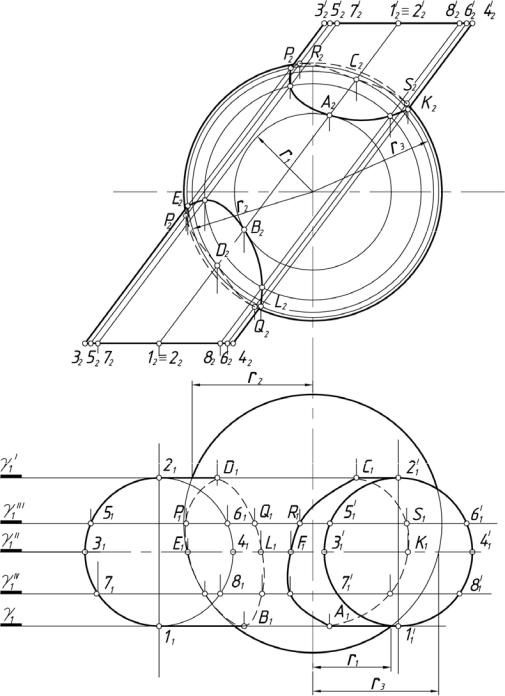
Пример 1. Построить линию пересечения поверхности сферы с наклонной цилиндрической поверхностью (рис. 13)
Рис. 13
34
Анализ
На чертеже задана сферическая поверхность и поверхность эллиптического цилиндра с круговым основанием и осью i 2.
Поверхности не имеют общей плоскости симметрии (это означает, что главные меридианы не пересекаются), но имеют простейшие линии, которыми являются: на цилиндре – прямолинейные образующие, на сфере
– окружности, плоскости которых параллельны 2. Попарное сочетание образующих цилиндра и окружностей на сфере определяют вспомогательные плоскости, параллельные 2.
Вспомогательные плоскости в данном примере могут быть параллельны и плоскости 1 (например ), потому что такие плоскости пересекают сферу по параллелям, а цилиндрическую – по окружностям, плоскости которых параллельны основанию цилиндрической поверхности, а центры принадлежат ее оси.
Последовательность решения на чертеже
Построение начинают с определения опорных точек.
Самые ближние точки А и В найдены при помощи вспомогательной плоскости (горизонтальный след 1), которая проведена через самую ближнюю образующую цилиндра 11 ( 1 1111 ) и пересекает сферу по окружности радиусом r1. Фронтальная проекция этой окружности пересекает фронтальную проекцию образующей 1212 цилиндрической поверхности в точках А2 и В2. Чтобы определить А1 и В1, проводят линии связи из А2 и В2 до пересечения со следом 1.
Аналогично находят точки C и D при помощи секущей плоскости (горизонтальный след 1 ), которую проводят через самую дальнюю образующую цилиндрической поверхности 22 ( 1 2121 ).
Фронтальная проекция образующей 2222 пересекает окружность, получившуюся в сечении сферы (радиус r2) в точках C2 и D2. Горизонтальные проекции C1 и D1 принадлежат 1 и определяют с помощью линий связи, проведенных через C2 и D2. C1 и A1 являются границами видимости линии пересечения на 1.
Точки E, F, K, L, являющиеся границами видимости на 2, определяют при помощи плоскости (горизонтальный след 1 ), которую проводят через главный меридиан цилиндрической поверхности – 33 и 44 , ( 1 3131 = 4141 ), фронтальные проекции которых являются очерковыми.
Пересечение очерковых образующих цилиндрической поверхности на 2 с окружностью сферы (радиус r3) дает E2, F2, K2, L2, проведя линии связи от которых до 1 , отмечают E1, F1, K1, L1.
35
Характерными точками линии пересечения заданных поверхностей являются точки P, Q, R, S, принадлежащие главному меридиану сферы, которые определены при помощи вспомогательной секущей плоскости (горизонтальный след 1 ), проходящей через главный меридиан сферы, и точки M и N, принадлежащие экватору сферы, которые определены при помощи плоскости 1 (фронтальный след 2 X).
Горизонтальные проекции M1 и N1 получают в пересечении экватора сферы с окружностью, которая получается в сечении цилиндра плоскостью(центр O, радиус).
Для получения плавной линии найдено несколько промежуточных точек также при помощи фронтальных секущих плоскостей.
Полученные одноименные проекции точек соединены плавной линией. Причем, линия пересечения распалась на две части: верхнюю и нижнюю. На видимых участках линии пересечения при проецировании на 2
находятся точки E2, B2, L2 и F2, A2, K2.
При проецировании на 1 нижняя часть линии пересечения видима на участке M1T1N1 , а верхняя – на участке C1F1A1.
Пример 2. Определить линию пересечения цилиндрической и конической поверхностей (рис. 14)
Анализ
В рассматриваемой задаче цилиндрическая поверхность является горизонтально проецирующей. Поэтому горизонтальная проекция линии пересечения известна. Она совпадает с окружностью, являющейся горизонтальной проекцией (следом) цилиндрической поверхности. Задача сводится к построению недостающей фронтальной проекции линии пересечения как линии, принадлежащей ко второй поверхности, т. е. поверхности конуса.
Последовательность построений
1. Определяют горизонтальные проекции самой высокой (А1) и самой низкой (В1) точек. Для этого проводят плоскость ( 1 – горизонтальный след) через оси вращения поверхностей (s1 и i1) и отмечают точки пересечения следа этой плоскости 1 со следом цилиндрической поверхности.
2. Отмечают горизонтальные проекции точек, принадлежащих главному меридиану цилиндра (C1 и D1) и главному меридиану конической поверхности (K1 и L1). Так как главный меридиан цилиндрической поверхности расположен впереди главного меридиана конической поверхности, то фронтальные проекции точек C и D (C2 и D2) являются границами видимости линии пересечения при проецировании на 2.
36

Рис. 14
37
3.Отмечают горизонтальные проекции самой ближней (E1) и самой дальней (F1) точек линии пересечения.
4.Отмечают горизонтальные проекции точек (M1 и N1), принадлежащих меридиану конической поверхности, параллельному профильной плоскости проекций.
5.Определяют фронтальные проекции отмеченных точек. A2, B2, C2, D2, K2, L2, E2, F2 построены с использованием образующих конической поверхности. Так, через точку А1 проходит горизонтальная проекция образующей S111. Проведя линию связи из 11 до фронтальной проекции окружности основания, отмечают 12. 12S2 – фронтальная проекция образующей, которой принадлежит А2. А2 отмечают на 12S2, проведя линию связи из А1. Аналогично найдены B2, C2, F2. M2 и N2 найдены с использованием круговых сечений конической поверхности, горизонтальные проекции которых
проведены из центра S1 радиусами S1M1 и S1N1 до пересечения с главным меридианом конической поверхности в точках 91 и 101. Отметив на очерковых образующих фронтальные проекции 92 и 102, параллельно основанию конуса проводят фронтальные проекции этих круговых сечений, которые в пересечении с профильным меридианом дают точки M2 и N2 .
6.Находят достаточное количество промежуточных (случайных) точек, используя для этого либо образующие, либо круговое сечение конической поверхности.
7.Полученные проекции точек соединяют плавной кривой линией с учетом видимости. Видимый участок линии пересечения проходит через
точки C2, N2, D2.
Пример 3. Построить линию пересечения поверхностей закрытого тора и прямого кругового конуса (рис. 15)
Анализ
Заданные поверхности вращения имеют общую плоскость симметрии (горизонтальный след 1). Оси поверхностей принадлежат этой плоскости и пересекаются между собой в точке О.
При этих условиях для определения точек линии пересечения можно применить способ концентрических сфер.
Последовательность построений
1. Отмечают точки пересечения контуров фронтальных проекций по-
верхностей А2 и В2.
2. Проводят линии связи из А2 и В2 и на главном меридиане поверхностей (след плоскости симметрии 1) отмечают А1 и В1.
38

Рис. 15
39
3.Отмечают точку пересечения фронтальных проекций осей поверх-
ностей О2 и проводят из нее нормаль к поверхности конуса (перпендикуляр О212 к образующей) и нормаль к поверхности тора (О222).
4.Нормаль О232 принимают за радиус минимальной вспомогательной сферы (Rmin), т. к. О232 > О212 и проводят очерк минимальной сферы
радиусом Rmin.
5.Соединив точки пересечения очерка минимальной сферы с очерковыми образующими конуса и точки касания очерка минимальной сферы с очерком тора, получают проекции окружностей, по которым вспомогательная сфера пересекла поверхность конуса и коснулась поверхности тора.
6.Отмечают точку пересечения (С2) этих отрезков, которая одновременно принадлежит и конусу, и тору, т. е. их линии пересечения.
7.Проводят горизонтальную проекцию окружности касания (радиу-
сом R1) и на ней отмечают точки С1 и С1 , опустив линии связи из С2 и С2 . 8. Определяют фронтальные проекции промежуточных (случайных)
точек линии пересечения (D2, D2 , E2, E2 , K2, K2 ), используя вспомогательные сферы, радиусы которых должны быть больше, чем Rmin и меньше, чем
Rmax = O2A2.
9.Строят горизонтальные проекции этих точек, воспользовавшись параллелями, по которым вспомогательные сферы пересекают тор.
10.Соединяют плавной линией фронтальные проекции построенных
точек A2, K2, D2, C2, E2, B2, которая и будет фронтальной проекцией линии пересечения, причем, весь участок будет видимый, т. к. поверхности имеют общую плоскость симметрии и невидимый участок линии пересечения совпадает с видимым.
11.Определяют границы видимости линии пересечения при проеци-
ровании на 1. Для этого находят фронтальные проекции горизонтальных очерковых образующих (S141) и отмечают точку (F2 = F2 ) пересечения линии A2K2 … B2 и образующей S242. Проведя линию связи из F2 = F2 до S141
иS141 отмечают точки F1 и F1 , являющиеся границами видимости на 1.
12.Определяют видимость. При проецировании на 1 точка А видима, поэтому участок горизонтальной проекции линии пересечения содер-
жащий А1 (F1A1F1 ), также видимый.
13. Через построенные проекции точек F1, D1, … F1 проводят линию видимого контура, а через F1, C1, E1, … F1 – штриховую линию.
40
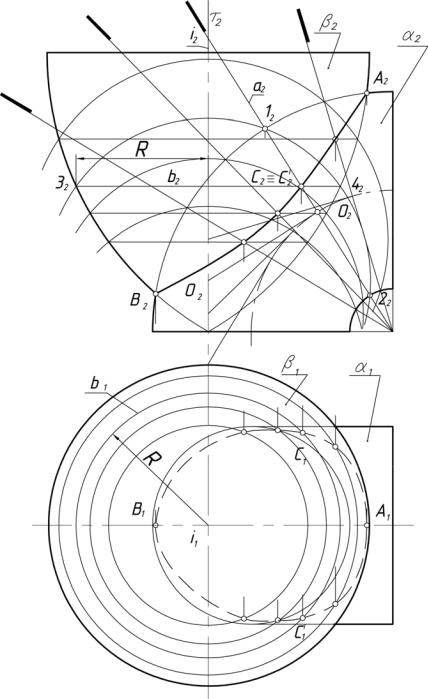
Пример 4. Построить линию пересечения открытого и закрытого торов (рис. 16)
Рис. 16
41
Анализ
Поверхности открытого ( ) и закрытого ( ) торов, заданные на чертеже, являются поверхностями вращения. Оси поверхностей (i и j) скрещиваются. Поверхности имеют общую плоскость симметрии (горизонтальный след 1), параллельную плоскости 2.
На поверхности открытого тора можно выделить семейство ок- ружностей-параллелей, плоскости которых параллельны 2 и перпендикулярны оси (j) открытого тора . Окружности второго семейства, принадлежащие поверхности тора , расположены в плоскостях, проходящих через ось (j) тора.
Поверхность закрытого тора содержит семейство окружностей, параллельных 1, и семейство дуг, являющихся меридианами тора .
При заданном расположении поверхностей нельзя подобрать ни одной плоскости, кроме общей плоскости симметрии, которая пересекала бы эти поверхности по простейшим линиям. Следовательно, способ секущих плоскостей-посредников для построения общих точек заданных поверхностей применять не рационально. Нельзя также применить и способ концентрических сфер, т. к. оси (i и j) заданных поверхностей не пересекаются.
Наиболее простым и точным при заданном расположении и характере поверхностей является способ эксцентрических сфер. В качестве заданного кругового сечения следует использовать сечение открытого тора плоскостью, проходящей через ось (j) тора.
Последовательность построений
1.Отмечают точки (А2 и В2) пересечения контуров поверхностей на 2.
2.Проводят фронтально проецирующую плоскость (фронтальный
след 2) через ось (j) поверхности тора (j2 2), которая пересечет тор по окружности а (фронтальная проекция а2 = 1222).
3.Из центра (О2) окружности а восставляют перпендикуляр (n2) и от-
мечают точку (О2 ) пересечения его с осью закрытого тора i (n2 ∩ i2 = O2 ).
4.Проводят очерк вспомогательной секущей сферы с центром в точке О2 и радиусом О2 12.
5.Соединяют отрезком (b2) точки пересечения (32 и 42) контура
вспомогательной секущей сферы с контуром закрытого тора . Отрезок b2
– фронтальная проекция окружности-параллели, по которой вспомогательная секущая сфера (с центром О2 ) пересекла этот тор.
6.Отмечают точки пересечения (С2 = С2 ) линий a2 и b2, которые и будут искомыми точками линии пересечения.
7.Проводят горизонтальную проекцию параллели b (b2) и на ней от-
мечают горизонтальные проекции точек С1 и С1 .
42
8.Построив аналогичным образом достаточное количество точек в зоне между точками А и В и соединив их одноименные проекции, получают проекции линии пересечения поверхностей.
9.Горизонтальная проекция линии пересечения полностью невиди-
ма, т. к. закрыта основанием поверхности .
10. Фронтальная проекция линии пересечения видима, т. к. невидимая ее часть совпадает (конкурирует) с видимой.
Пример 5. Построить линию пересечения поверхностей (рис. 17)
Анализ
Заданные поверхности вращения имеют общую плоскость симметрии (горизонтальный след 1), в которой расположены и пересекаются между собой оси вращения (i и j) этих поверхностей. Поверхности имеют семейства окружностей, расположенных в плоскостях, перпендикулярных осям вращения и в меридианных плоскостях.
Наиболее рациональным способом определения точек, принадлежащих линии пересечения поверхностей, является способ концентрических сфер. Но, определяя радиус минимальной секущей сферы, обнаруживаем, что сфера с минимальным радиусом оказывается вписанной в обе поверхности. Это дает возможность применить теорему Монжа и построить фронтальную проекцию линии пересечения, которая распадается на две плоские кривые, провести, отметив точки пересечения очерковых линий поверхностей (A2, B2, C2, D2) и точку (E2) пересечения линий касания поверхностей с вписанной вспомогательной сферой .
Последовательность построений
1.Отмечают точки пересечения контуров (очерковых линий) поверхностей на 2 (A2, B2, C2, D2).
2.Отмечают точку пересечения фронтальных проекций осей враще-
ния поверхностей (i2 ∩ j2 = O2) и определяют радиус минимальной секущей сферы. Нормали к поверхностям оказываются равными.
3.Из центра О2 радиусом Rmin проводят очерк вспомогательной сферы и, соединив точки касания очерка сферы с очерками заданных поверхностей (12 и22, 32 и 42), получают проекции линий касания а2 и b2.
4.Отметив точку пересечения линий касания E (E2 = a2 ∩ b2), проводят фронтальную проекцию линии пересечения, которая представляет собой два отрезка прямой, проходящих через точки A2, E2, C2 и B2,
E2, D2.
43

Рис. 17
5.Горизонтальную проекцию линии пересечения, которая состоит из
двух кривых, пересекающихся в точках Е1 и Е1 , проводят через проекции точек, построенных при помощи параллелей тора .
6.Проекции А1, В1, С1, D1 отмечены на следе 1 общей плоскости симметрии заданных поверхностей с помощью линий связи, проведенных из проекций А2, В2, С2, D2.
44
Методические рекомендации к выполнению задачи 03.02
Построить развертку одной из четырех поверхностей, представленных в задачах03.01. Нанестинаразверткулиниюпересеченияповерхностей.
Цель задачи – отработать способы построения разверток и закрепить навыки решения метрических задач.
Для успешного выполнения задания необходимо знать:
определение и свойства разверток поверхностей;
какиеповерхностиявляютсяразвертываемые, какиенеразвертываемые;
какие развертываемые поверхности имеют точную, а какие приближенную развертку;
способы построения точных и приближенных разверток;
приемы построения условных разверток неразвертываемых поверхностей;
способы определения натуральных величин отрезков прямой и плоских фигур.
Рассматриваемая задача относится к классу метрических задач. Точную развертку имеют только гранные поверхности. Универ-
сальным способом построения разверток гранных поверхностей являет-
ся способ триангуляции (треугольников). Сущность этого способа заключается в том, что определяют натуральные величины ребер треугольных граней и по ним строят натуральные величины этих граней. Когда грани имеют более трех сторон (4-угольные, 5-угольные и т. д.), их диагоналями разбивают на треугольники и, определив натуральные величины сторон этих треугольников, находят натуральную величину всей грани.
Пример 1. Построить развертку пятиугольной
пирамиды SABCDE и определить положение точки М на развертке, принадлежащей поверхности пирамиды (рис. 18)
Анализ
Основание заданной пирамиды расположено горизонтально. Следовательно, ребра основания пирамиды проецируются без искажения на 1. Боковые ребра не являются линиями уровня. Поэтому для решения задачи необходимо определить их натуральные длины. Это можно сделать любым из известных способов определения натуральной величины отрезка прямой общего положения, например, вращением вокруг проецирующей оси.
45

46
Рис. 18
Последовательность построений
1.Рассекают боковую поверхность пирамиды по одному из боковых ребер SB.
2.Определяют натуральные величины боковых ребер, для этого:
проводят ось вращения i 1 (i1 = S1, i2 OX);
горизонтальные проекции боковых ребер S1A1, S1B1, S1C1, S1D1, S1E1 поворачивают вокруг i1 = S1 до положения, параллельного оси
проекции OX (S1A1 , S1B1 ,…);
через точки A1 , B1 , C1 , D1 , E1 проводят линии связи и отмечают точки A2 , B2 , C2 , D2 , E2 пересечения их с фронтальной проекцией основания пирамиды;
соединяют A2 , B2 , C2 , D2 , E2 с S2 и получают отрезки S2A2 , S2B2 , S2C2 , S2D2 , S2E2 , которые равны натуральным величинам соответ-
ствующих ребер.
3.На свободном поле чертежа строят SAB, SAE, SED, SDC,SCB с общей вершиной S и сторонами, равными натуральной величине
ребер (SA = S2A2 , SB = S2B2 , AB = A1B1), так, чтобы каждый следующий треугольник имел общую сторону с предыдущим.
4.К одному из звеньев ломаной BAEDCB (CB) пристраивают основание пирамиды. Для этого:
горизонтальную проекцию основания A1B1C1D1E1 разбивают диагоналями A1C1, A1D1 на три треугольника A1B1C1, A1C1D1, A1D1E1;
строят CBA0 = C1B1A1 так, чтобы C1B1 совпадала с CB, CA0D0 =
= C1A1D1 так, чтобы C1A1 совпадала с А0, и A0D0E0 = A1D1E1 так, чтобы A1D1 совпадала с A0D0.
Фигура, ограниченная ломаной SBAEDCD0E0A0BS является полной разверткой пирамиды SABCDE.
5. Для нанесения на развертку точки М, принадлежащей поверхности пирамиды, выполняют следующие построения:
на отрезке ВА откладывают отрезок В1 = В111 и проводят прямую S1, которой принадлежит точка М;
способом вращения определяют натуральную величину отрезка
SM (S2M2 );
на отрезке S1 откладывают отрезок SM = S2M2 .
Способ перпендикулярного сечения применяют для построения раз-
вертки призматических поверхностей, у которых боковые ребра являются линиями уровня (параллельны одной из плоскостей проекций 1 или 2).
Сущность этого способа состоит в том, что плоскость сечения, перпендикулярная боковым ребрам, оказывается перпендикулярной той плоскости проекций, которой боковые ребра параллельны, и поэтому проекция
47
плоскости сечения вырождается в прямую линию, перпендикулярную проекциям боковых ребер. Построив вторую проекцию сечения и определив натуральную величину его сторон, получают натуральные величины расстояний между боковыми ребрами в гранях.
Пример 2. Построить развертку призмы ABCDEF (рис. 19)
Анализ
Боковые ребра AF, BE, CD призмы параллельны плоскости проекций 2. Это видно из того, что горизонтальные проекции их A1F1, B1E1, C1D1 параллельны оси проекций OX (или перпендикулярны линиям связи BB1, CC1, …). Поэтому для построения развертки можно применить способ перпендикулярного (нормального) сечения.
Последовательность построений
1. Через произвольную точку на одном из боковых ребер проводят след ( 2) секущей плоскости перпендикулярно фронтальным проекциям боковых ребер A2F2, B2E2, C2D2. В качестве такой точки можно использо-
вать вершину (С2) ( 2 В2Е2).
2. Отмечают точки (12, 22) пересечения следа этой плоскости с проекциями ребер и горизонтальные проекции этих точек 11, 21 соответственно на B1E1 и A1F1.
3.Вращают след 2 до положения параллельного оси проекции ОХ
иотмечают новые проекции точек (12 , 22 и 11 , 21 ).
4.На свободном поле чертежа проводят прямую линию и на ней от-
кладывают отрезки 1020 = 11 21 , 20С0 = 21 С1, С010 = С111 .
5.Через точки 10, 20, С0, 10 проводят прямые, перпендикулярные
кпрямой.
6.На проведенных перпендикулярах откладывают отрезки: 10Е0 =
= 12Е2, = 12В2, 20F0 = 22F2, 20A0 = 22A2, C0D0 = C2D2.
7.Строят F0E0D0 (F0E0 = E0F0, D0E0 = D0E0) верхнегооснованияпризмы.
8.Строят A0C0B0 (A0B0 = A0B0, C0B0 = C0B0) нижнегооснованияпризмы. Фигура, ограниченная замкнутой ломаной A0B0E0F0E0D0E0B0C0B0A0,
является полной разверткой заданной призмы. Линии сгибов обозначают на развертках штрихпунктирной линией.
Способ раскатки применяют для построения развертки призматических поверхностей, у которых боковые ребра являются линиями уровня, а основание принадлежит плоскости уровня. В основе способа – способ вращения вокруг линии уровня.
48
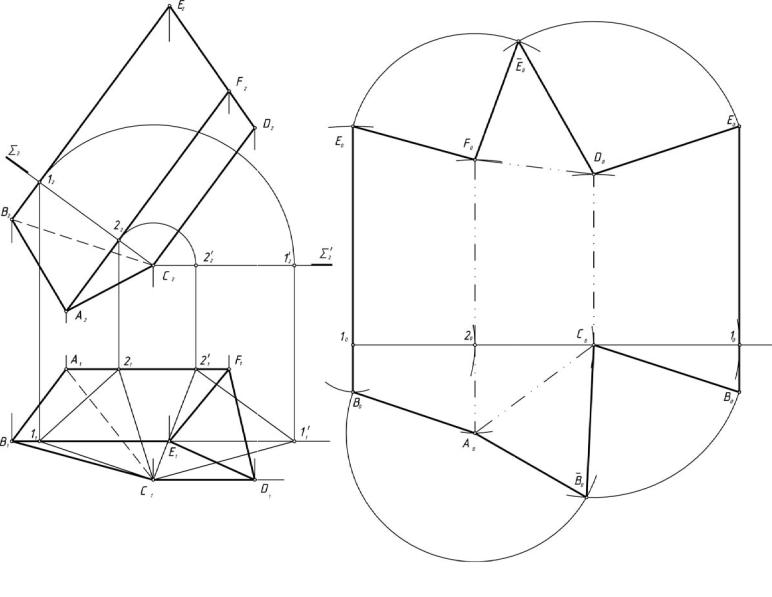
49
Рис. 19
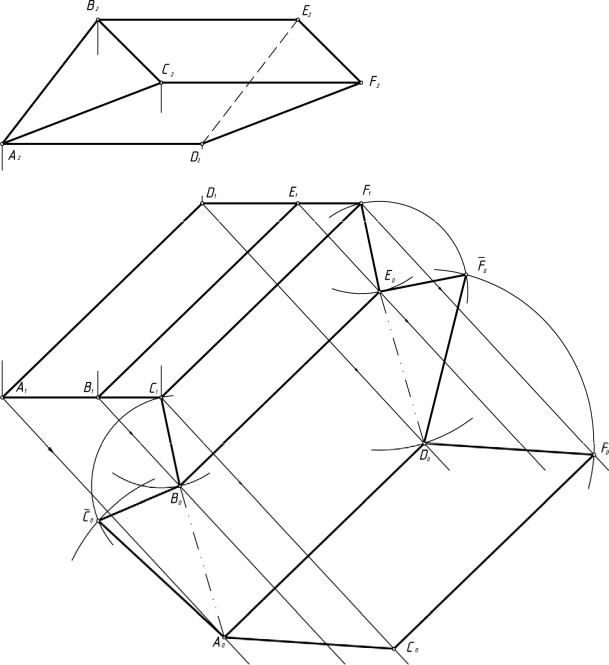
Пример 3. Построить развертку наклонной треугольной призмы ABCDEF (рис. 20)
Рис. 20
50
Анализ задачи
Боковые ребра AD, BE, CF заданной призмы параллельны горизонтальной плоскости проекций (A2D2 C2F2 B2E2 OX) и проецируется на нее в натуральную величину. Основания АВС и DEF призмы параллельны фронтальной плоскости проекций 2 и стороны основания проецируются в натуральную величину на 2.
Боковое ребро можно принять за ось вращения вокруг которой раскатывают боковую поверхность до совмещения с плоскостью.
Последовательность построений
1.Черезгоризонтальныепроекциивершинпризмы(точкиА1, В1, С1, … F1) проводят прямые, перпендикулярные горизонтальным проекциям ребер
A1D1, B1E1, C1F1, являющиеся следами плоскостей вращения точек A, B, C,
D, E, F.
2.Радиусом, равным натуральной стороне ребра (FE = F2E2) из центра F1 делают засечку на перпендикуляре, проведенном из Е1 (F1E0 = F2E2)
иотмечают точку Е0. На перпендикуляре из В1 делают засечку радиусом, равным В2С2 (С1В0 = В2С2), и отмечают точку В0. Точку В0 можно было получить, проведя из Е0 прямую, параллельную горизонтальным проекциям боковых ребер, и отложить отрезок Е0В0 = Е1В1.
3.На перпендикуляре из точки D1 делают засечку радиусом, равным натуральной величине стороны ED (E0D0 = E2D2).
4.На перпендикуляре, проведенном из точки F1, делают засечку радиусом D0F0 = D2F2 из центра D0.
5.Проводят D0A0 C0F0 C1F1.
6.Строят натуральные величины оснований призмы E0D0F0 и
А0В0С0, причем E0F0 = F1E0; D0F0 = D0E0; B0C0 = B0C1; A0С0 = А0С2.
Фигура, ограниченная замкнутой ломаной линией C1F1E0F0D0F0A0B0C1 является разверткой призмы.
Приближенную развертку имеют линейчатые поверхности: цилиндрические, конические. Принцип построения таких разверток заключается в том, что в линейчатую поверхность вписывают гранную поверхность (пирамиду, призму) большим количеством боковых граней (чем больше граней, тем точнее развертка). Выполняют развертку вписанного многогранника и принимают ее за приближенную развертку линейчатой поверхности.
51
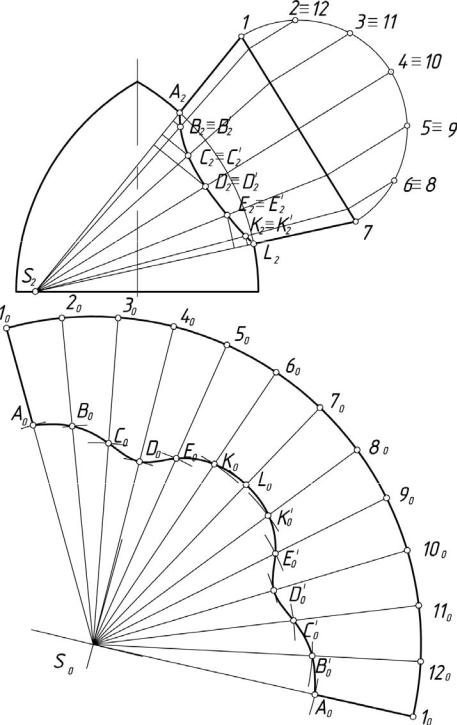
Пример 4. Выполнить развертку конической
и торовой поверхностей и нанести на развертку линию пересечения поверхности тора и конуса (рис. 21)
Рис. 21
52
Анализ задачи
На чертеже задан прямой круговой конус. Для построения развертки его поверхности в конус вписывают правильную пирамиду и ее развертку принимают в качестве приближенной развертки конической поверхности.
Последовательность построений
1.Проводят полукруг основания, который занимает проекцию основания на плоскость, перпендикулярную оси вращения конуса.
2.Делят его на 6 равных частей и отмечают точки 1, 2, 3, … .
3.На свободном поле чертежа отмечают точку S0 и проводят дугу радиусом, равным длине образующей конуса (1S2), с центром в точке S0.
4.На проведенной дуге отмечают произвольную точку 10 и откладывают от нее на дуге отрезки 1020, 2030, 3040, …, равные соответственно хор-
дам 12, 23, 34, … .
5.Полученные на дуге точки 10, 20, 30, … соединяют с точкой S0. Получившийся сектор круга является приближенной разверткой боковой поверхности конуса.
6.Проводят окружность основания конуса, касательный дуге развертки боковой поверхности.
7.Отмечают точки пересечения образующих конуса, проведенных через точки деления окружности основания с линией пересечения поверх-
ностей (A, B, B C, C ,…).
8. Определяют натуральные величины участка каждой образующей от вершины до точки пересечения (SA, SB, …). Наиболее удобным способом определения натуральной длины здесь является способ вращения вокруг проецирующей прямой, в качестве которой берут ось вращения конуса. Переместив каждую точку параллельно основанию конуса до крайней образующей, получают на последней натуральную длину участка (S2D2). На соответственной образующей развертки откладывают отрезки, равные натураль-
ным величинам S0D0 = S2D2, S0B0 = S2B2, … S0A0 = S2A2, … S0L0 = S2L2, … .
9. Полученные точки A0, B0, C0, … соединяют плавной линией, которая и будет разверткой линии пересечения.
Пример 5. Построить развертку поверхности закрытого тора инанестинаразвертку линиюпересеченияегосконусом(рис. 22)
Анализ задачи
Закрытый тор имеет неразвертываемую поверхность. Общий прием построения условной развертки такой поверхности заключается в том, что поверхность разбивают на некоторое число равных частей, которые затем вписывают в поверхности (или описывают около поверхности), имеющей точную или приближенную развертку. Выполняют развертку отсеков описываемой (или вписанной) поверхности и принимают за условную развертку данной неразвертываемой поверхности.
53
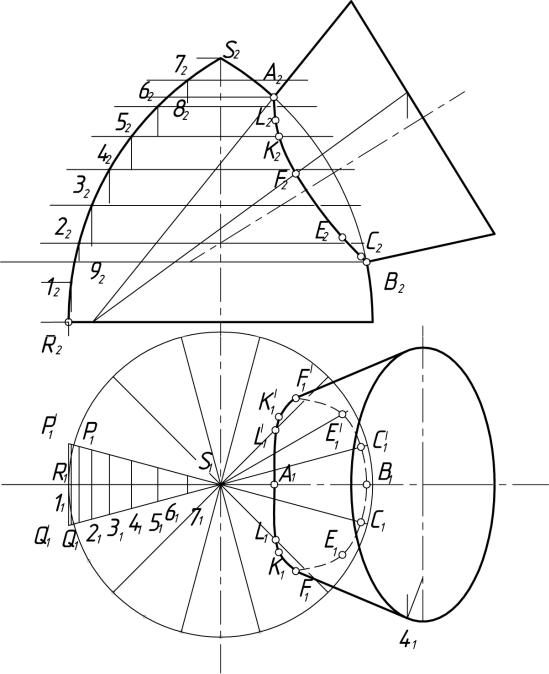
Рис. 22
Последовательность построений
1.Горизонтальную проекцию поверхности тора (круг) разбивают, например, на 12 равных частей (рис. 23).
2.Одну двенадцатую часть вписывают в отсек цилиндрической по-
верхности. Дуга P1Q1 при этом спрямляется в отрезок прямой P1 Q1 (образующую цилиндра, описывающего одну двенадцатую часть поверхности тора).
54
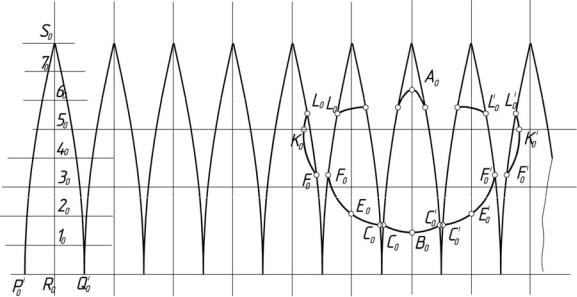
Рис. 23
3.Проекцию меридиана R2S2 делят на 8 равных частей и через горизонтальные проекции точек деления 11, 21, 31, …, 71 проводят в пределах отсека цилиндрической поверхности отрезки прямых, длина которых приближенно равна длине дуг параллелей тора, проходящих через точки деления.
4.На свободном поле чертежа проводят прямую и откладывают на
ней 12 отрезков, равных отрезку P1 Q1 (рис. 23).
5. Через середины отрезков проводят перпендикуляры к прямой и на
них откладывают отрезки R010 = R212, 1020 = 1222, …, 70S0 = 72S2. Длина отрезка R0S0 приближенно равна длине меридиана RS.
6.Через точки 10, 20, 30, …, 70 проводят прямые, параллельные первой прямой и откладывают на них отрезки образующих описывающего цилиндрического отсека, проходящие через проекции 11, 21, 31, …, 71.
7.Соединяют конечные точки этих отрезков плавными кривыми линиями и получают 12 отсеков условной развертки боковой поверхности тора.
8.На соответствующих меридианах и образующих, заменяющих параллели тора, определяют положение отдельных точек линии пересечения
на развертке. Например, точку В0 отмечают на главном меридиане соответствующего отсека развертки на расстоянии, равном отрезку главного ме-
ридиана 2282 ниже параллели, проходящей через точку 20; точка С0 принадлежит параллели, проходящей через 20, и границе отсека; точка D0 принадлежит главному меридиану на расстоянии, равном отрезку меридиана
3292 и т. д.
9. Определив достаточное количество точек, их соединяют отрезками плавных кривых.
55
Варианты заданий 03
Варианты заданий 03 представлены в табл. 4.
Таблица 4
56
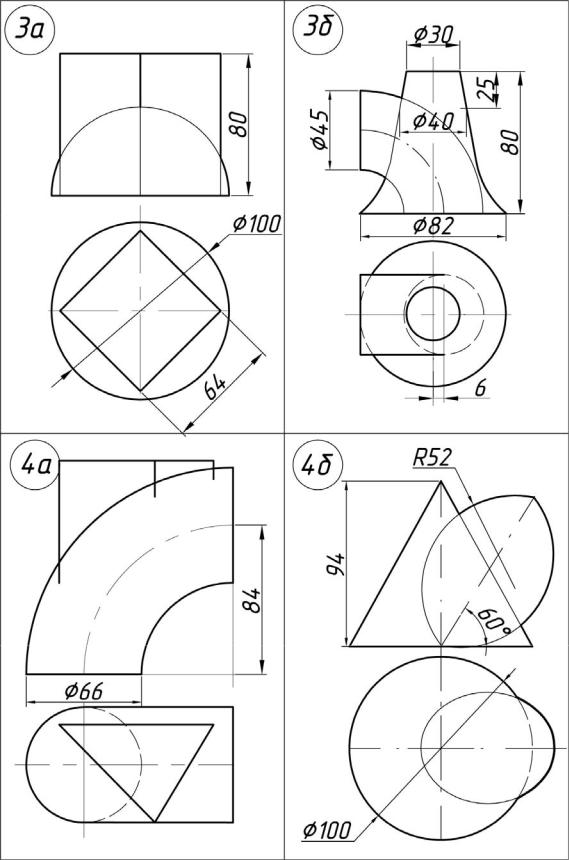
Продолжение табл. 4
57

Продолжение табл. 4
58
Продолжение табл. 4
59

Продолжение табл. 4
60
Продолжение табл. 4
61
Продолжение табл. 4
62
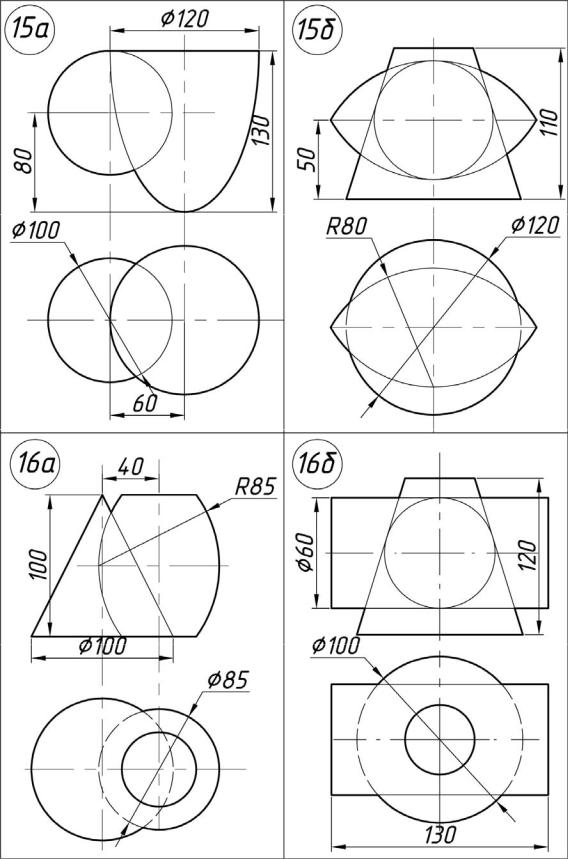
Продолжение табл. 4
63
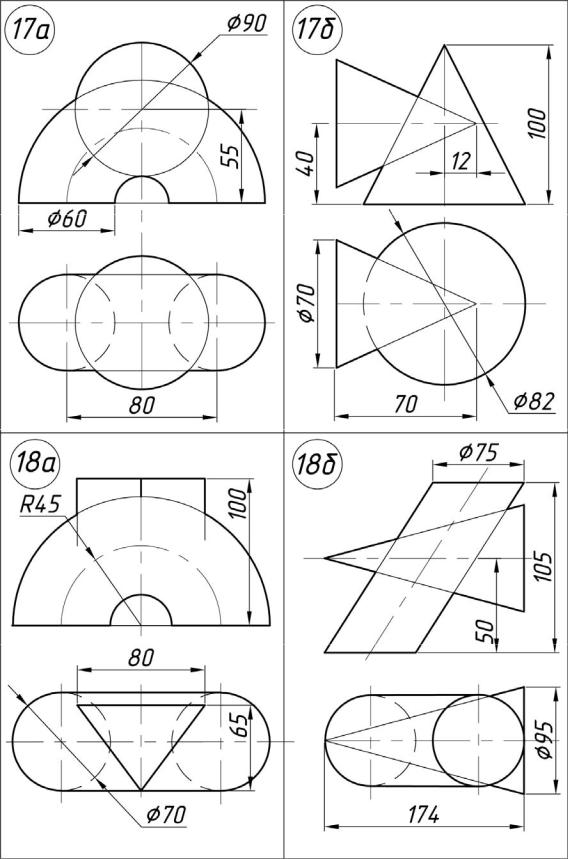
Продолжение табл. 4
64
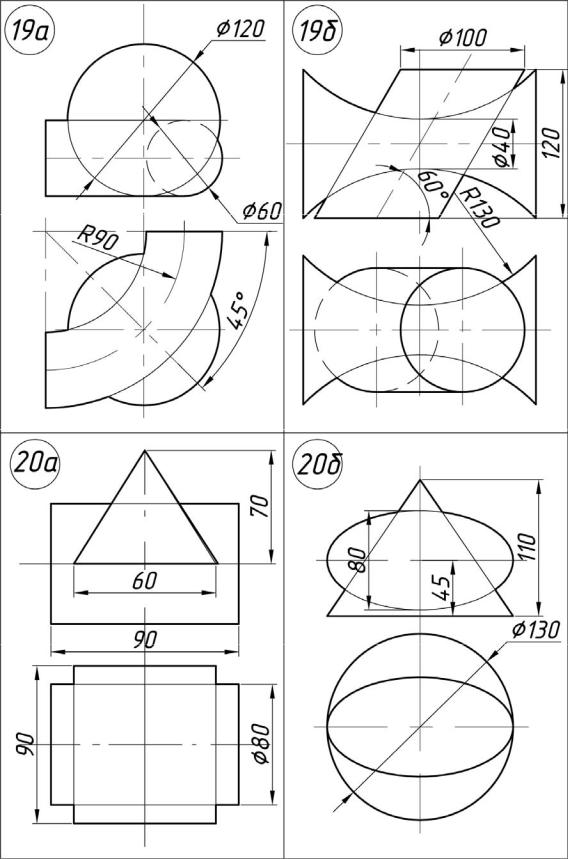
Продолжение табл. 4
65
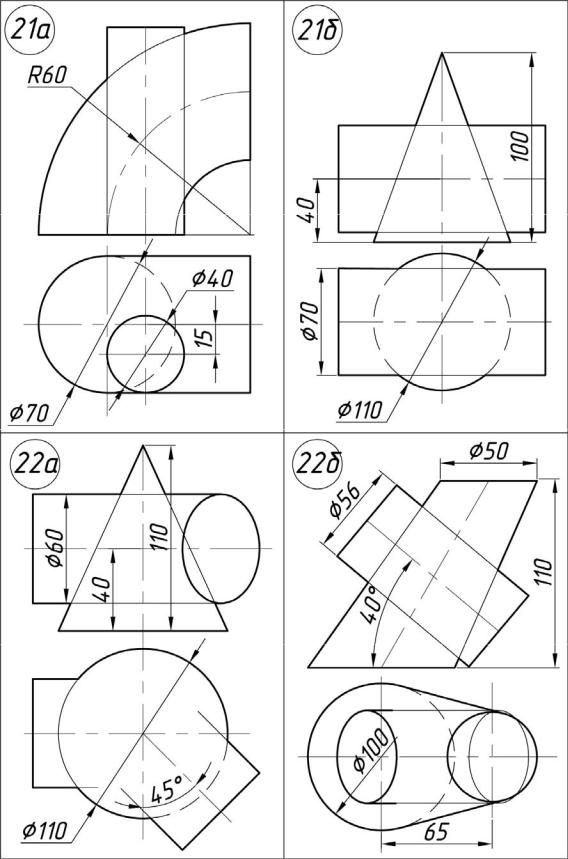
Продолжение табл. 4
66

Продолжение табл. 4
67

Продолжение табл. 4
68
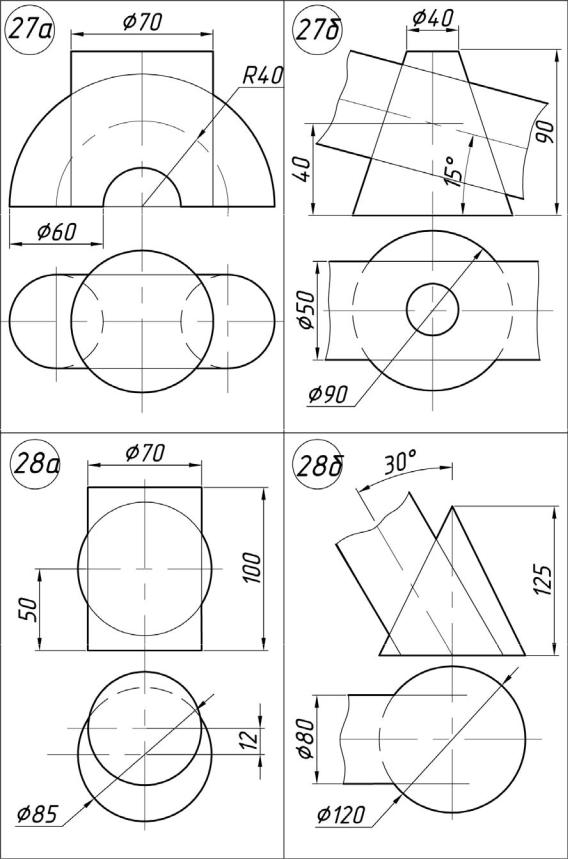
Продолжение табл. 4
69
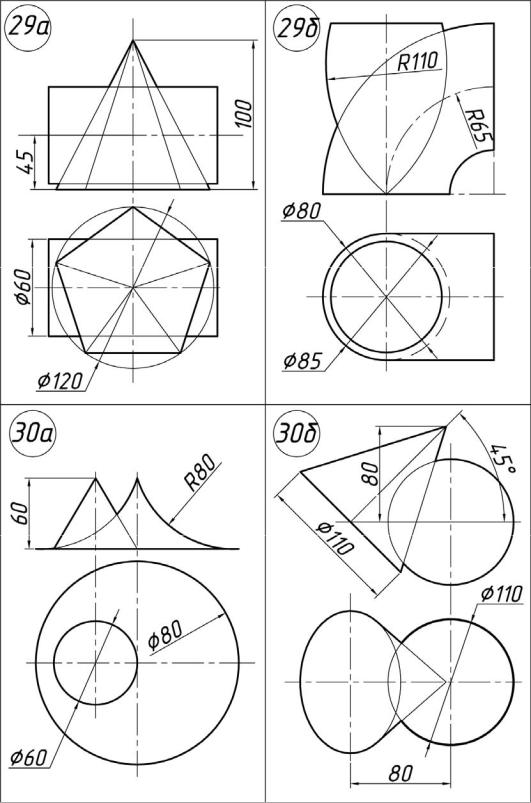
Продолжение табл. 4
70
