17. Теорема Вариньона

Теорема Вариньона. Если рассматриваемая плоская система сил приводится к равнодействующей, то момент этой равнодействующей относительно какой-либо точки равен алгебраической сумме моментов всех сил данной системы относительно той же самой точки. Предположим, что система сил приводится к равнодействующей R, проходящей через точку О. Возьмем теперь в качестве центра при­ведения другую точку O₁. Главный момент (5.5) относительно этой точки равен сумме моментов всех сил в общем виде: M_O1=ƩM_o1(F_k). В нашем случае, имеем M_O1=M_Ol(R), так как главный момент для центра приведения О равен нулю (M_O=0). Сравнивая соотношения , получаем M_O1(R)=ƩM_Ol(F_k); ч.т.д.

18.Аналитический способ задания силы Выберем систему координат Oxyz. Вектор можно построить, зная модульи углымежду вектором и соответствующими осями Задание этих величин и определяет силу. Точка приложения силы должна быть задана дополнительно координатами х, у, z. Кроме того, силу можно задавать проекциями на оси. Тогда

Эти формулы позволяют, зная проекции силы на оси координат найти ее модуль и углы с осями, т.е. определить силу. Зная проекции, можно построить вектор геометрически.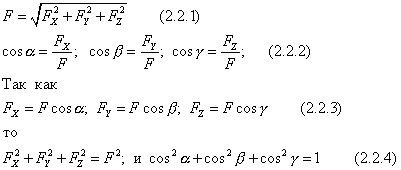

Для плоскости формулы (2.2.1) и (2.2.2) запишутся Построение в плоскости производится по 4-й аксиоме статики.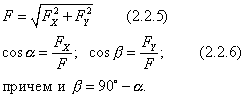

19. Опорные устройства балочных систем

Применяются следующие виды опор:

Шарнирно - подвижная опора

Здесь остается неизвестным числовое значение опорной реакции RA. Следует отметить, что опорная поверхность шарнирно-подвижной опоры может быть непараллельна оси балки (рис.б). Реакция RA в этом случае не будет перпендикулярна оси балки, так как она перпендикулярна опорной поверхности.

 

Шарнирно - неподвижная опора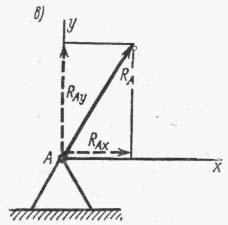

Эта опора допускает поворот вокруг оси шарнира, но не допускает никаких линейных перемещений. В данном случае известна только точка приложения опорной реакции — центр шарнира; направлениеи значение опорной реакции неизвестны. Обычно вместо определения значения и направления (полной)реакции RA находят ее составляющие RAx и RAy.

 Жесткая заделка (защемление)Такая опора не допускает ни линейных перемещений, ни поворота.Неизвестными в данном случае являются не только значение и направление реакции, но и точка ее приложения. Поэтому жесткую заделку заменяют силой реакции RA и парой сил с моментом MA.

Для определения опорной реакции следует найти три неизвестных: составляющие RAx и RAy опорной реакции по осям координат и реактивный момент MA.

20.Проекция силы на ось и на плоскость

Скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы называется проекцией силы на ось.

Знак плюс проекция имеет, если перемещение от начала к концу происходит в положительном направлении оси, и знак минус если в отрицательном.

Таким образом, проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу.

Проекция силы на ось Ох обозначается какTo есть проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.

Если сила перпендикулярна оси, то ее проекция на эту ось равна нулю.

Проекцией силы на плоскость Оху называется вектор, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 13).

Проекция силы на плоскость есть величина векторная и характеризуется как модулем, так и направлением в плоскости Оху. Модуль проекции силы на плоскость Оху выражается какТогда проекции на оси Ох и Оу:

21. разложение сил. Разложить данную силу на не­сколько составляющих — значит найти такую систему нескольких сил, для которой данная сила является равнодействующей. Эта задача является неопределенной и имеет однозначное решение лишь при задании дополнительных условий. Рассмотрим два частных случая:

а) разложение силы по двум заданным на­правлениям. Задача сводится к построению такого парал­лелограмма, у которого разлагаемая сила является диагональю, а стороны параллельны заданным направлениям

б)разложение силы по трем заданным на­правлениям. Если заданные направления не лежат в одной плоскости, то задача"является определенной и сводится к построе­нию такого параллелепипеда, у которого диагональ изображает заданную силу R, а ребра параллельны заданным направлениям. Способом разложения можно в простейших случаях пользовать­ся для определения сил давления на связи. Для этого действующую на тело (конструкцию) заданную силу надо разложить по направле­ниям реакции связей, так как согласно закону о действии и противо­действии сила давления на связь и реакция связи направлены вдоль одной и той же прямой.