
- •1.Разложение сил. Два частных наиболее важных случаях
- •2. Связи и их реакции. Привести примеры основных случаев
- •3. Записать аналитические условия равновесия плоской системы сходящихся сил.Теорема о трех силах.
- •4.Условия равновесия произвольной плоской системы сил. Три формы.
- •5.Приведение произвольной плоской системы сил к данному центру.
- •6.Сложение пар сил в пространстве.Условия равновесия пар
- •7.Три формы равновесия произвольной плоской системы сил. Области применения.
- •8. Теорема о паралельном переносе силы. Доказательство.
- •12. Пара сил. Момент пары.
- •17. Теорема Вариньона
- •19. Опорные устройства балочных систем
- •20.Проекция силы на ось и на плоскость
- •22.Связи и их реакции. Аксиома связей
- •24. Равнодействующая сходящихся сил и условие их равновесия
- •25. Мощность и кпд
- •27.Скорость
- •33. Силы инерции твердого тела
- •34. Понятие о плоскопараллельном движении твердого тела
- •35. Силы инерции при прямолинейном и криволинейном движении материальной точки
- •36. Теоремы о сложении скоростей и ускорений точки при сложном движении
- •37.Принцип Даламбера
1.Разложение сил. Два частных наиболее важных случаях
Разложение силы на составляющие основывается на правилах сложения сил.
Целью разложения силы, приложенной к какому-либо телу, является определение сил взаимодействия между этим телом и другими телами, обычно связями, наложенными на него. Чтобы разложить силу, нужно задать некоторые из характеристик (величина, направление и точка приложения) составляющих сил. Точками приложения составляющих сил могут быть: 1) точка приложения раскладываемой силы и 2) точка соединения или соприкосновения тела, к которому приложена раскладываемая сила, с другими телами (связями). Направлениями для составляющих сил в большинстве случаев являются: 1) направления, по которым другие тела (связи) препятствуют перемещению тела или точки приложения раскладываемой силы, и 2) направления движения точки приложения раскладываемой силы или точек приложения составляющих сил.
Составляющие Р1 и Р2 силы Р по двум заданным направлениям АВ и АС определяются сторонами параллелограмма, построенного на этих направлениях и силе Р как его диагонали.
При разложении силы Р на две параллельные составляющие силы Р1 и Р2, надо различать два случая:
1) точки приложения составляющих лежат по разные стороны от силы Р и
2) эти точки расположены по одну сторону от нее. В первом случае составляющие силы направлены в одну сторону и по величине равны:
P1=(b/(a+b))P; P2=(a/(a+b))P;
во втором случае составляющие Р1 и Р2 направлены в противоположные стороны и по величине равны:
P1=(b/(a-b))P; P2=(a/(a-b))P.
Разложение силы на две параллельные можно применять, например, при определении сил давления Q1 и Q2 вала на подшипники от веса маховика (фиг.23; а и б). Давление вала на подшипник:
Q1=P1;Q2=P2.
2. Связи и их реакции. Привести примеры основных случаев
Рассмотрим наиболее часто встречающиеся в механике типы связей и их реакции.
1.2.1. Идеально гладкая поверхность
Реакция
идеально гладкой поверхности (без учета
трения) направлена по общей нормали к
поверхностям соприкасающихся твердых
тел (рис. 1.1,а). Если одна из поверхностей
вырождается в точку, то реакцию следует
направить по нормали к другой поверхности
(например, реакции ![]() и
и![]() ,
рис. 1.1,б).
,
рис. 1.1,б).
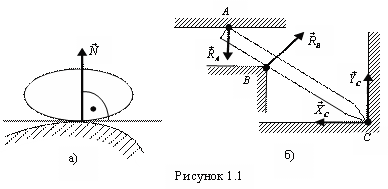
Когда
тело упирается острием в угол (см. рис.
1.1,б), связь препятствует перемещению
острия как по горизонтали, так и по
вертикали. Реакция в точке ![]() для
этого случая может быть представлена
двумя составляющими
для
этого случая может быть представлена
двумя составляющими![]() и
и![]() .
Модуль реакции находят по формуле
.
Модуль реакции находят по формуле
![]() .
.
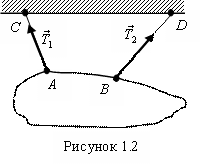
1.2.2. Гибкая нерастяжимая нить
Реакция
нити направлена от объекта равновесия
вдоль нее так, что нить натянута. Например,
реакции нитей ![]() и
и![]() (рис.
1.2) направлены вдоль нитей к точкам их
подвеса
(рис.
1.2) направлены вдоль нитей к точкам их
подвеса![]() и
и![]() .
Они не позволяют точкам
.
Они не позволяют точкам![]() и
и![]() удаляться
соответственно от точек
удаляться
соответственно от точек![]() и
и![]() .
.
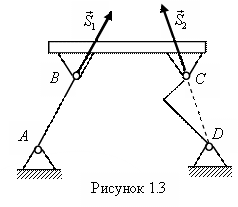
1.2.3. Идеальный стержень
Идеальным
называют жесткий невесомый стержень,
имеющий на концах шарниры (рис. 1.3). Такая
связь препятствует перемещению тела
только вдоль прямой, соеди-няющей
шарниры. Поэтому реакции прямого ![]() и
изогнутого
и
изогнутого![]() стержней
направлены вдоль линий, соединяющих
шарниры
стержней
направлены вдоль линий, соединяющих
шарниры![]() и
и![]() ,
,![]() и
и![]() .
.
1.2.4. Цилиндрическая шарнирно-подвижная опора
Цилиндрическая
шарнирно-подвиж-ная опора (рис. 1.4) –
каток – препятствует перемещению
закрепленной точки тела по перпендикуляру
к плоскости, на которой она расположена.
Реакция такой связи ![]() направлена
по нормали к плоскости I-I.
направлена
по нормали к плоскости I-I.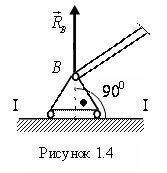
1.2.5. Цилиндрическая шарнирно-неподвижная опора
Шарнирно-неподвижная
опора (рис. 1.5) – шарнир – позволяет телу
поворачиваться вокруг оси шарнира, но
препятствует перемещению закрепленной
точки в плоскости, перпендикулярной
этой оси. Поэтому реакция такой связи
может быть представлена силой ![]() ,
которая лежит в указанной плоскости.
Направление реакции заранее неизвестно.
Чаще всего реакцию раскладывают на две
составляющие, направленные параллельно
выбранным осям:
,
которая лежит в указанной плоскости.
Направление реакции заранее неизвестно.
Чаще всего реакцию раскладывают на две
составляющие, направленные параллельно
выбранным осям:![]() и
и![]() (см.
рис. 1.5,а) или
(см.
рис. 1.5,а) или![]() и
и![]() ,
,![]() и
и![]() (см.
рис. 1.5,б).
(см.
рис. 1.5,б).
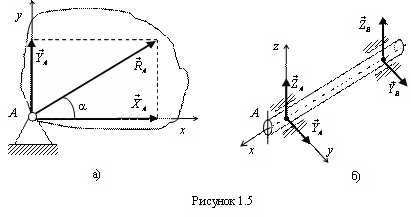
1.2.6. Сферический шарнир и подпятник
Сферический
шарнир (рис. 1.6) – это связь, которая
позволяет телу поворачиваться вокруг
некоторой точки, но препятствует
перемещению точки в любом направлении.
Поэтому реакция такого шарнира
представлена тремя составляющими: ![]() ,
,![]() ,
,![]() (см.
рис. 1.6,а).
(см.
рис. 1.6,а).
Аналогично
обстоит дело и с реакцией подпятника
вала (точка ![]() ,
см. рис. 1.6,б), который препятствует
перемещению этой точки в трех взаимно
перпендикулярных направлениях. В
точке
,
см. рис. 1.6,б), который препятствует
перемещению этой точки в трех взаимно
перпендикулярных направлениях. В
точке![]() вал
закреплен с помощью подшипника (см. рис.
1.6,б), составляющие реакции которого
изображены в соответствии с п. 1.2.5.
вал
закреплен с помощью подшипника (см. рис.
1.6,б), составляющие реакции которого
изображены в соответствии с п. 1.2.5.
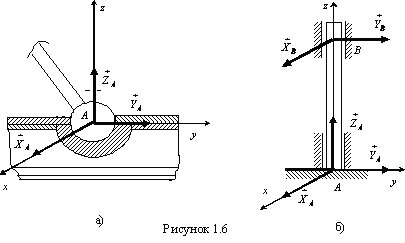 1.2.7. Жесткое
защемление (заделка)
1.2.7. Жесткое
защемление (заделка)
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.
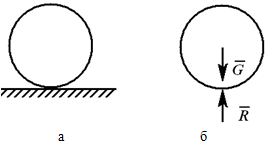
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня)
Примерами могут служить: 1)Шарнирно-неподвижная опора, 2)Шарнирно-подвижная опора,3) Соединение стержня и втулки
1)2)3)
