
- •Оглавление
- •Предмет инженерной графики
- •Рекомендации по выполнению заданий
- •Условные обозначения
- •1. Методы проецирования
- •1.1. Свойства прямоугольного проецирования
- •1.2. Теорема о частном случае проецирования прямого угла
- •2. Комплексный чертёж точки (эпюр Монжа)
- •Вопросы для самопроверки
- •3. Проекции прямой
- •3.1. Прямые уровня
- •3.2. Проецирующие прямые
- •3.3. Взаимное расположение двух прямых
- •3.4. Определение натуральной величины отрезка
- •Вопросы для самопроверки
- •4. Плоскость
- •4.1. Проецирующие плоскости
- •4.2. Плоскости уровня
- •4.3. Главные (характерные) линии плоскости
- •4.4. Прямые и точки, лежащие в плоскости
- •4.5. Условие параллельности прямой линии плоскости
- •4.6. Условие параллельности двух плоскостей
- •Вопросы для самопроверки
- •5. Оформление чертежей
- •5.1. Форматы
- •5.2. Оформление поля чертежа, основная надпись
- •5.3. Масштабы чертежей, линии, шрифты чертёжные, штриховка в разрезах и сечениях
- •Линии чертежа
- •Шрифты чертёжные
- •5.4. Нанесение размеров, знаки, надписи на чертежах
- •6. Геометрические построения
- •7. Аксонометрия
- •7.1. Построение овала
- •8. Изоображения предметов
- •8.1. Виды
- •8.2. Разрезы
- •8.3. Сечения
- •9. Резьбовые изделия и соединения
- •9.1. Основные определения и параметры резьбы, условные изображения и обозначения резьб
- •9.2. Крепежные изделия
- •9.3. Изображение резьбовых соединений
- •9.4. Болтовые соединения
- •9.5. Шпилечные соединения
- •10. Эскизы и рабочие чертежи
- •11. Сборочный чертеж
- •12. Типичные ошибки в графических работах
- •Приложение
- •Список литературы
4.2. Плоскости уровня
Плоскости уровня – плоскости, параллельные одной из плоскостей проекций (дважды проецирующие) На комплексном чертеже две проекции их имеют вид прямой, расположенной под прямым углом к линиям связи, а третья проекция даёт изображение всех элементов, лежащих в этой плоскости в натуральную величину (Н.В), (рис. 12):
а) горизонтальная плоскость уровня А1В1С1– Н.В,
б) фронтальная плоскость уровня А2В2С2– Н.В,
в) профильная плоскость уровня А3В3С3– Н.В.
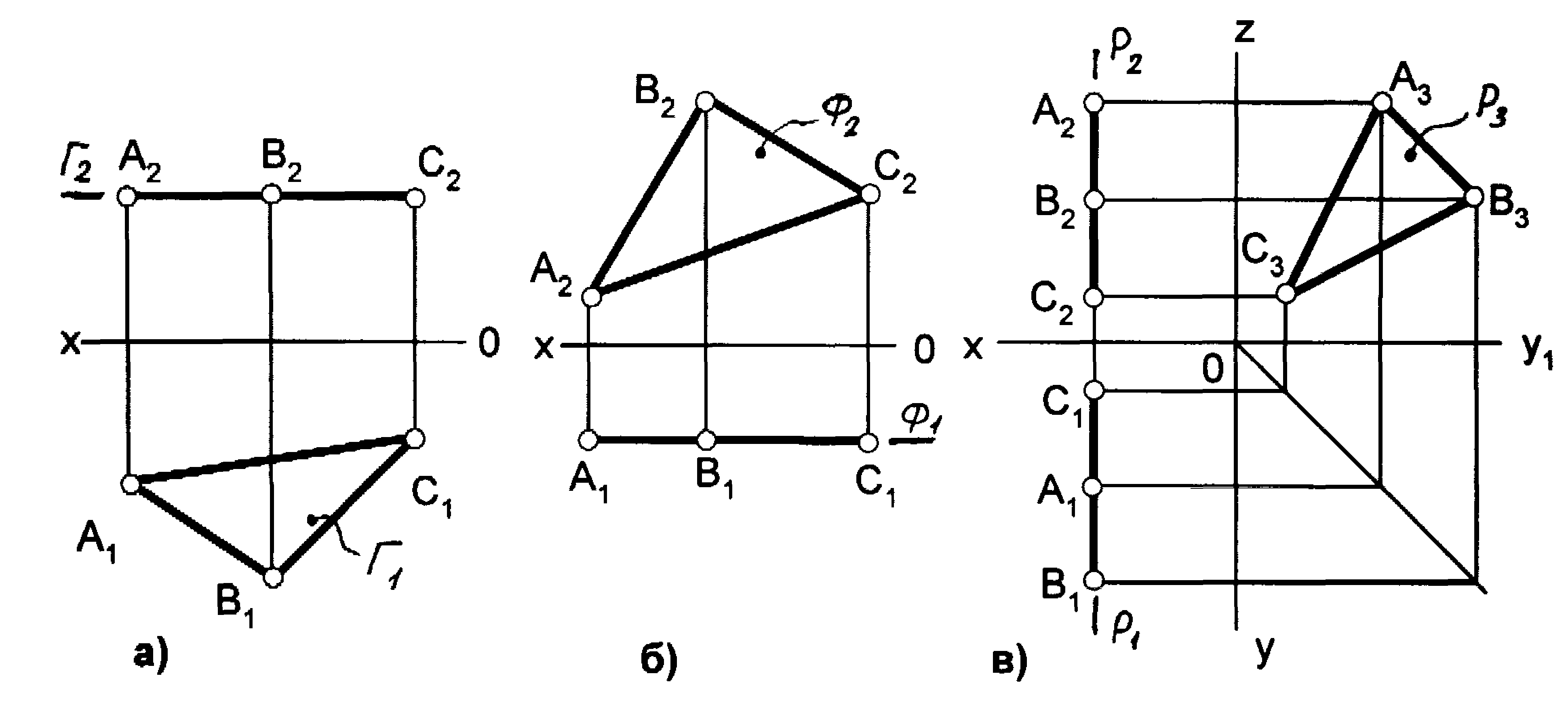
Рис. 12
4.3. Главные (характерные) линии плоскости
В любой плоскости можно построить линии, параллельные плоскостям проекций. Их называют линиями уровня плоскости Горизонталь плоскости -это линия в плоскости, параллельная горизонтальной плоскости проекций. Для построения горизонталиh= А1 в плоскости АВС (рис. 13) вначале проводят фронтальную проекциюh2= А212горизонтали, она всегда перпендикулярна линиям связи. Затем находят горизонтальную проекциюh1= А111искомой горизонтали. А1АВС, так как две ее точки принадлежат этой плоскости, и является горизонталью, так как по построению она параллельна горизонтальной плоскости проекций (рис. 13).
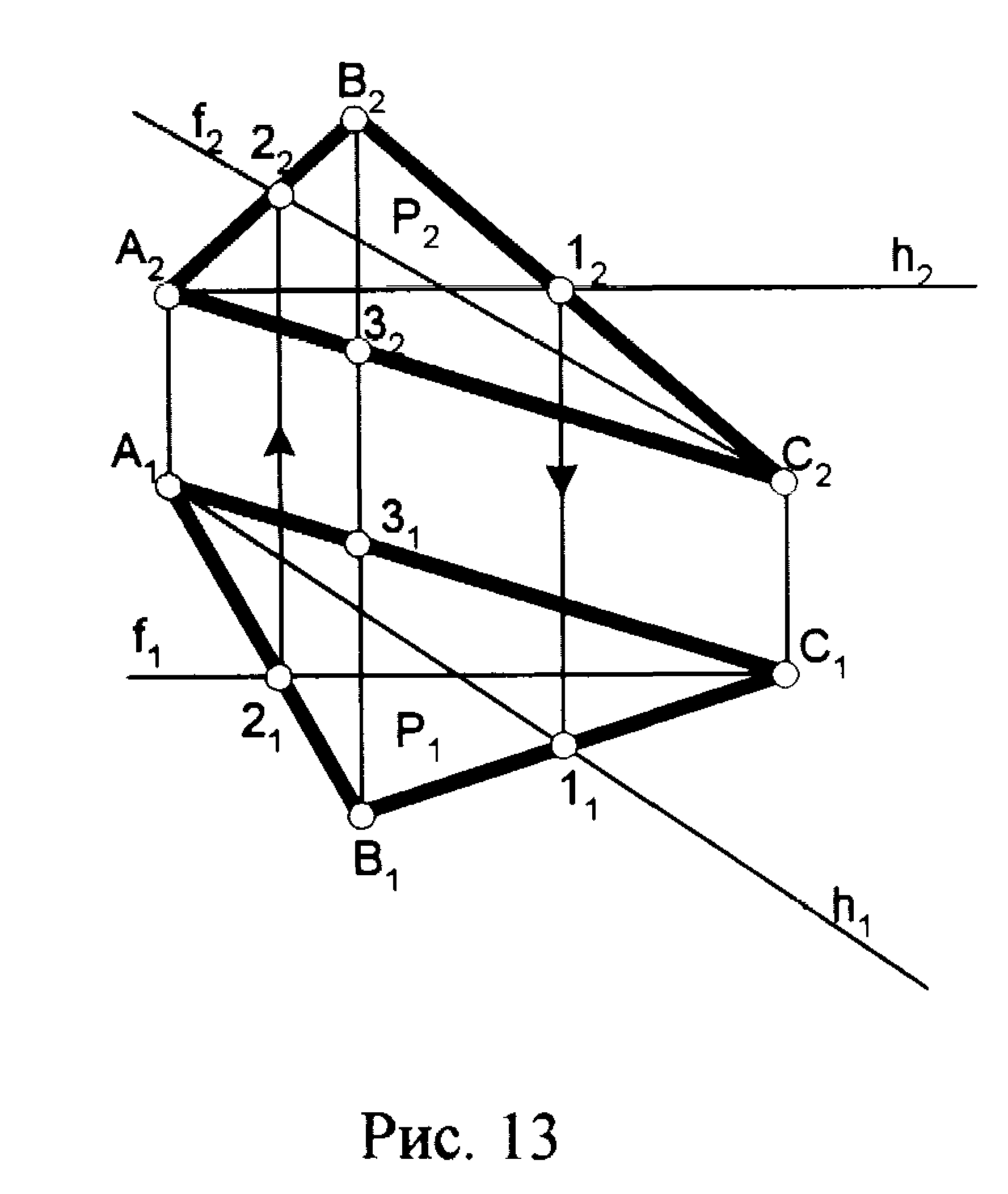
Рис. 13
Фронталь плоскости – прямая, принадлежащая и параллельная фронтальной плоскости проекций. Построение фронталиf в плоскости АВС аналогично построению горизонтали, но вначале проводят горизонтальную проекциюf1= С121фронтали (рис. 13), затем фронтальную проекцию. Прямая, лежащая в плоскости и параллельная профильной плоскости проекций, называется профильной прямой Р плоскости (рис. 13). Для плоскостей частного положения соответствующие прямые уровня также являются и проецирующими. Например, у горизонтально-проецирующей плоскости (рис. 11) её фронтали одновременно являются и горизонтально-проецирующими прямыми.
4.4. Прямые и точки, лежащие в плоскости
Признаки принадлежности точки и прямой плоскости:
1. Точка принадлежит плоскости, если через неё можно провести в этой плоскости линию, например прямую 1 (рис. 14, а). КАВС => К1 и 1АВС.

Рис. 14
2. Прямая принадлежит плоскости, если она проходит через две точки этой плоскости (рис. 13).
4.5. Условие параллельности прямой линии плоскости
Прямая параллельна плоскости, если в плоскости можно провести прямую, параллельную данной плоскости.
На рис. 14задана плоскость(АВС). Эта задача имеет бесчисленное множество решений. Например, в плоскости(АВС) проводят произвольную прямую 1–2, а затем через точку К – искомую прямую КL, ей параллельную (рис. 14, б).
4.6. Условие параллельности двух плоскостей
Известно, что две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
У параллельных плоскостей горизонтали и фронтали взаимно параллельны.
Вопросы для самопроверки
1. Как задаётся плоскость на комплексном чертеже ?
2. Какие плоскости называются проецирующими ? Перечислить свойства таких плоскостей.
3. Какие плоскости называются плоскостями уровня ?
4. Сформулировать правило определения взаимного расположения прямой и плоскости:
а) принадлежность прямой плоскости;
б) пересечение прямой и плоскости;
в) параллельность прямой и плоскости.
5. Перечислить характерные (главные) линии плоскости.
6. Перечислить признаки принадлежности точки и прямой плоскости.
7. Сформулировать условие параллельности прямой и плоскости.
8. Сформулировать условие параллельности двух плоскостей.
