Вопросы для самопроверки

1. В чём заключается сущность метода проекций ?

2. Какими плоскостями ограничены четверти пространства ?

3. По каким осям пересекаются плоскости проекций ?

4. Что называется комплексным чертежом точки ?

5. Что такое линия связи ?

3. Проекции прямой

Прямая может быть задана аналитически (уравнением) и графически (проекциями). На чертежах прямую линию задают проекциями двух её точек.

Образование комплексного чертежа прямой аналогично образованию комплексного чертежа точки.

Прямые относительно плоскостей проекций занимают такие положения: общее, уровня,проецирующее.

Прямые, не параллельные ни одной из плоскостей проекций, называются прямыми общего положения. Все проекции прямой общего положения не параллельны и не перпендикулярны линиям проекционной связи чертежа (рис. 5).

Рис. 5

3.1. Прямые уровня

Прямые, параллельные горизонтальной, фронтальной или профильной плоскостям проекций, называют соответственно горизонталь, фронталь, профильная прямая. Это – линии уровня.

Проекция отрезка прямой уровня на параллельную ему плоскость равна натуральной величине (НВ) отрезка, а углы, которые составляет эта проекция с линиями проекционной связи, равны углам между самими отрезками и непараллельными им плоскостями проекций (рис. 6). Здесь– угол наклона прямой к плоскости проекций П₁,– угол наклона прямой к плоскости проекций П₂,– угол наклона прямой к плоскости проекций П₃.

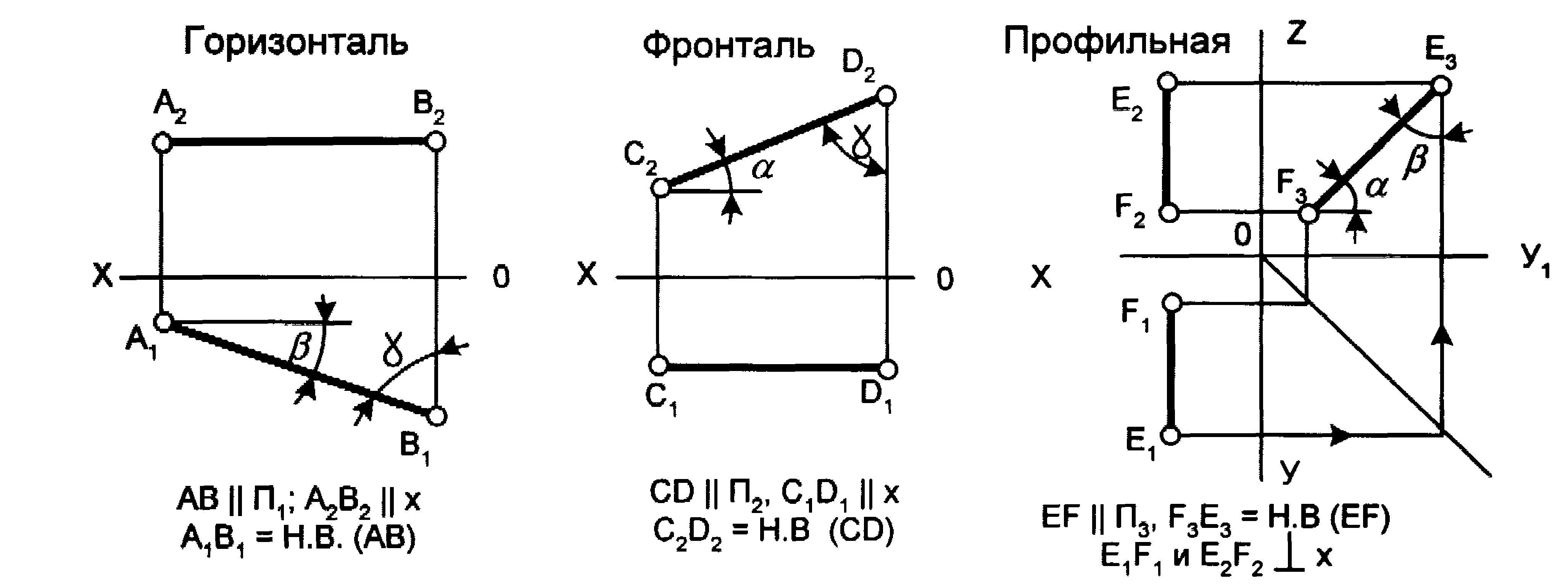
Рис. 6

3.2. Проецирующие прямые

Проецирующие прямые – это прямые, перпендикулярные одной из плоскостей проекций. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции совпадают на чертеже с направлением линии связи (рис. 7).

Рис. 7

Точки проецирующих прямых называют конкурирующими относительно соответствующих плоскостей проекций. Точки А и В,С и D, Е иFбудут конкурирующими относительно П₁; П₂; П₃. Конкурирующие точки применяют при определении видимости на чертежах. Из двух горизонтально конкурирующих точек А и В на плоскости П₁видима та, которая выше, то есть А, а точка В оказывается под точкой А. Из двух фронтально конкурирующих точек С иD(рис. 7) на плоскости П₂видима та, которая ближе к наблюдателю, то есть точкаD, а точка С невидима, так как расположена за точкойD.

Из двух профильно конкурирующих точек Е и F(рис. 7) на плоскости П₃, видима та, которая левее, то есть точка Е.

3.3. Взаимное расположение двух прямых

Две прямые в пространстве могут пересекаться, скрещиваться и быть параллельными

Пересекающиеся прямые – прямые, имеющие одну общую точку пересечения (аb= М,рис. 8, а). Следовательно, на основании свойства проецирования на комплексном чертеже точки М₁и М₂пересечения одноименных проекций прямых должны находиться на одной линии связи.

Рис. 8

Параллельные прямые – прямые, пересекающиеся в бесконечно удалённой точке (с || d,рис. 8, б). Следовательно, на основании свойства проецирования на комплексном чертеже одноименные проекции прямых должны быть параллельными.

Скрещивающиеся прямые – прямые, не имеющие общей точки (mиn,рис. 8, в). Следовательно, на основании свойства проецирования на чертеже точки пересечения одноименных проекций прямых не должны принадлежать одной линии связи.