3. Определение собственных и взаимных сопротивлений Задача 3.1

В Т-образной схеме требуется найти сопротивления ,,, выразив их через параметры схемы.

Рис. 3.1

Закорачиваем ветвь источника 2, задаемся током и определяем напряжение в точке 1.

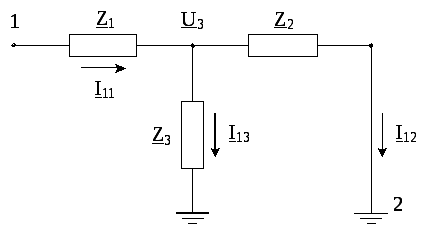
Рис. 3.2

,

,

,

,

,

.

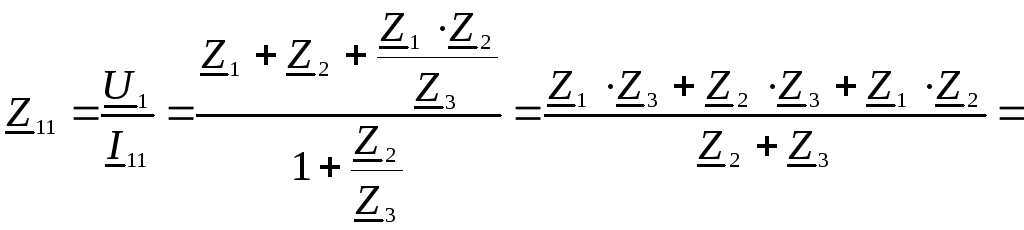
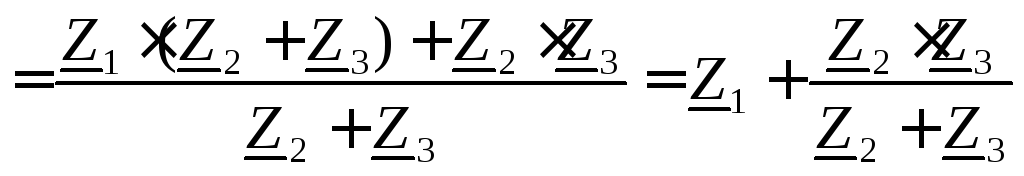Аналогичным путем, закорачиваем ветвь источника 1, задаваясь током , и определяя напряжение в точке 2, можно найти

,

.

Схема рис. 3.1 находит широкое применение в расчетах, поэтому студентам предлагается запомнить формулы.

При этом обращается внимание на то, что в такой простой схеме нет необходимости в применении метода единичных токов. Собственное сопротивление , например, можно получить непосредственно из рис. 3.2 путем параллельного и последовательного сложения сопротивлений схемы. Взаимное сопротивление схемынаходится однократным преобразованием «звезды» в «треугольник».

Задача 3.2

В схеме (рис. 3.3) требуется определить знак углов сопротивлений и.

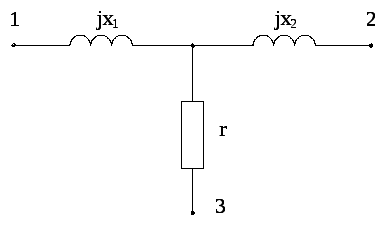
Рис. 3.3

Решение

Угол > ; следовательно, дополнительный угол < 0.

Это приводит к сдвигу максимума угловой характеристики мощности в подобных схемах (т. е. параллельное включение активного сопротивления) в сторону углов меньше . Отрицательная активная составляющая свидетельствует о том, что взаимное сопротивление не является некоторым физическим сопротивление схемы, а лишь коэффициентом пропорциональности между напряжением и током различных ветвей, имеющим размерность сопротивления. В отличие от него собственное сопротивлениеисточника 1 является входным сопротивлением со стороны схемы, у которой ветвь источника 2 закорочена. Поэтому в данной схеме активная составляющаяможет быть только положительной, а> 0.

Задача 3.3

В схеме (рис. 3.4) определить .

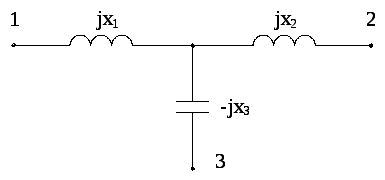
Рис. 3.4

Решение

.

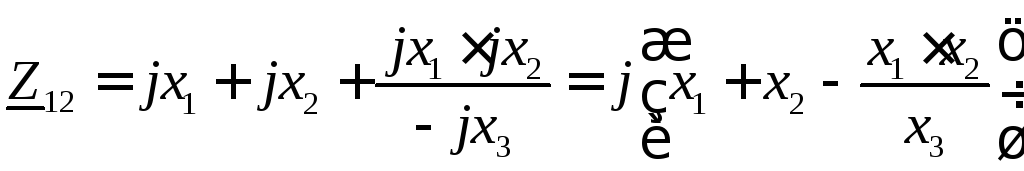Включение параллельной емкости уменьшает величину взаимного сопротивления.

Задача 3.4

Требуется определить влияние реактора, включенного в начале линии, на идеальный предел мощности электропередачи (рис. 3.5).

Рис. 3.5

Исходные данные в относительных единицах:

; ;; ; ; ; ; ; .

Составляем схему замещения (рис. 3.6)

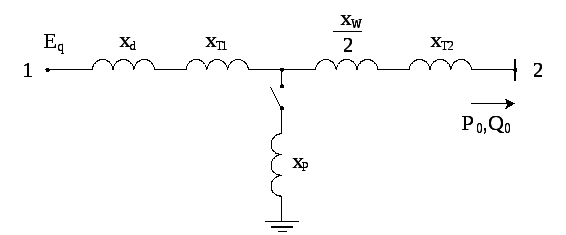
Рис. 3.6

Определяем предел мощности в схеме без реактора.

, ,

,

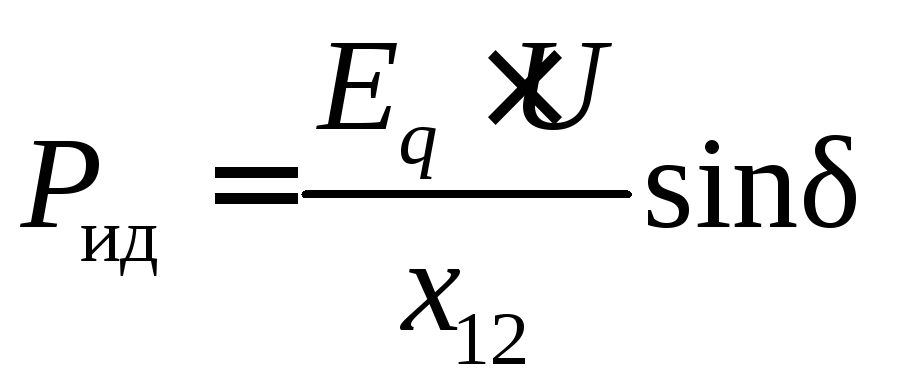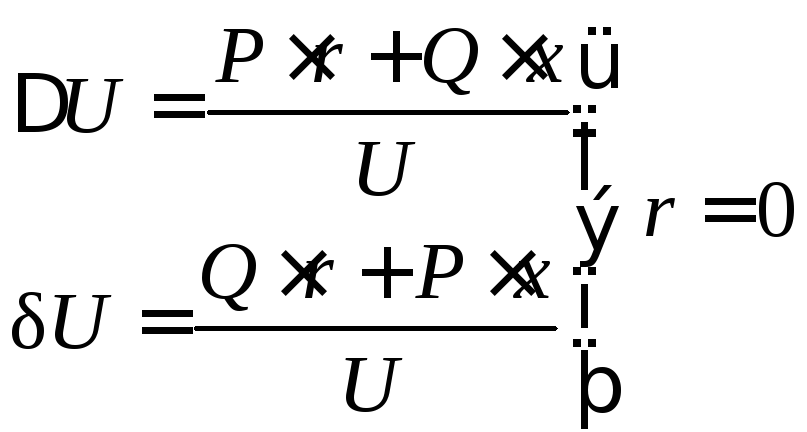, где ,,,

;

;

;

%.

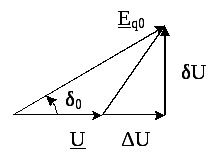
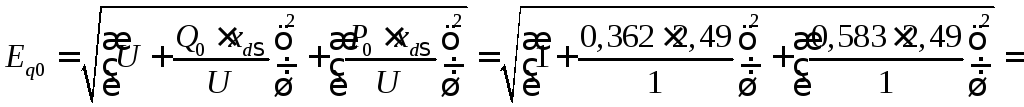
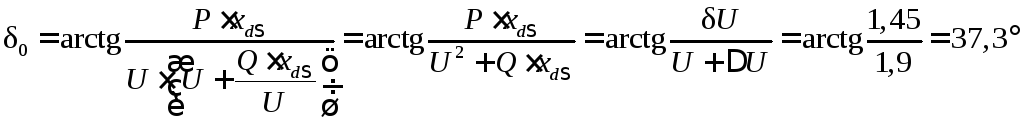
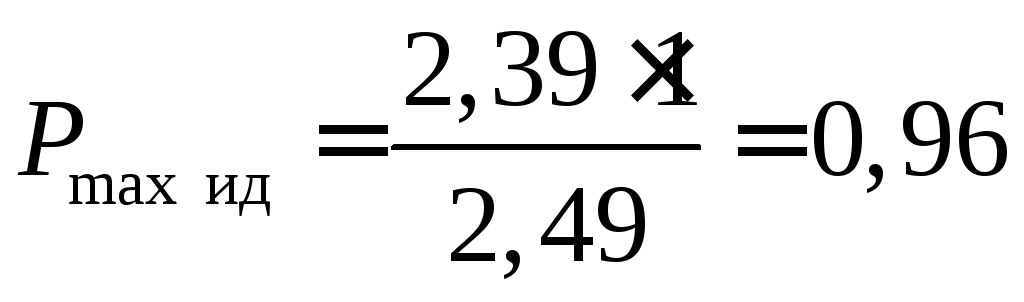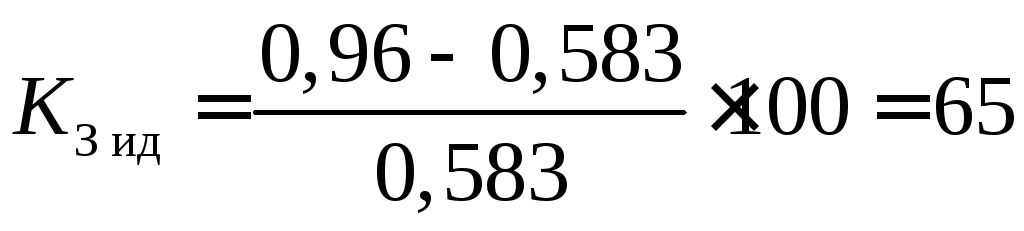Определим предел мощности в схеме с реактором (рис. 3.7)

Рис. 3.7

Реактивная мощность на входе сопротивления

,

.

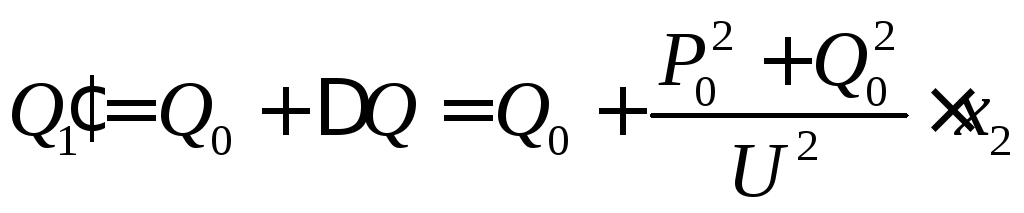Напряжение в точке включения реактора

;

.

Мощность реактора

.

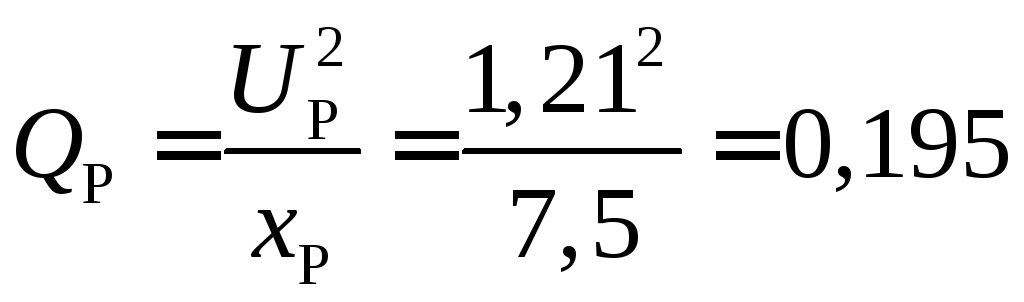Реактивная мощность на выходе сопротивления

.

ЭДС генератора

;

.

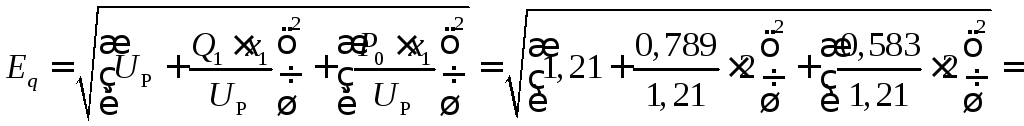
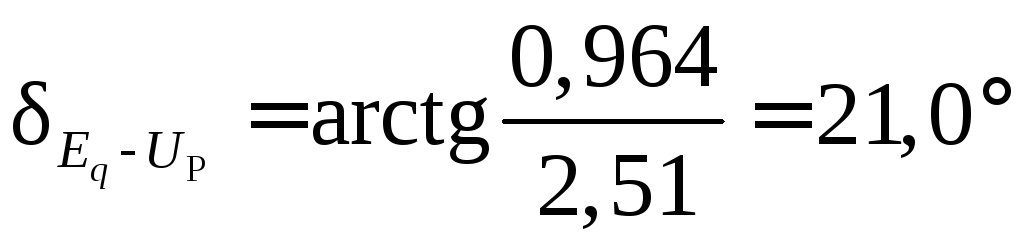Суммарный угол сдвига ЭДС машины относительно вектора напряженияU

.

Взаимное сопротивление

.

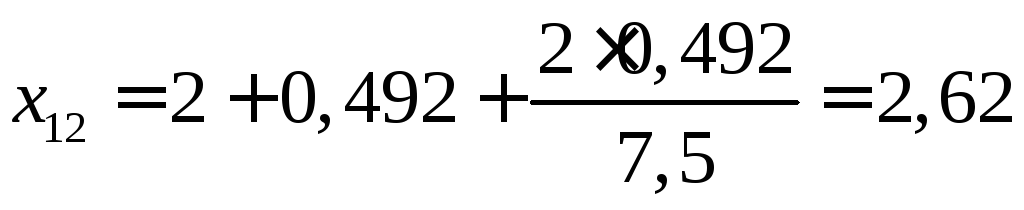Предел мощности и коэффициент запаса

;

%.

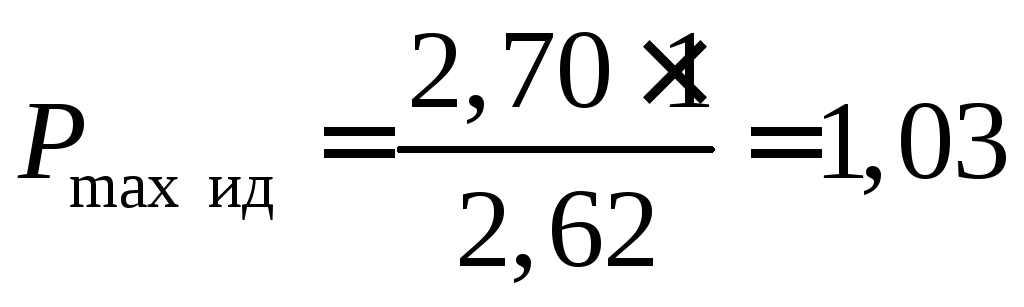При заданной постановке задачи предел мощности увеличился, поскольку несмотря на увеличение взаимного сопротивления при включении реактора (2,49→2,62), ЭДС генератора возросла в большей степени (2,39→2,70). Последнее связано с необходимостью значительно увеличить ток возбуждения генератора в схеме с включенным реактором. Задача может быть дана и в другой постановке, когда и в том, и в другом случае (есть реактор или нет) возбуждение генератора не меняется (const). При этом меняется величина мощности , поступающей в приемную систему, а предел мощности без реактора выше, чем при нём. При увеличении мощности реактора , видимо, предел мощности должен меняться так, как показано на рис. 3.8.

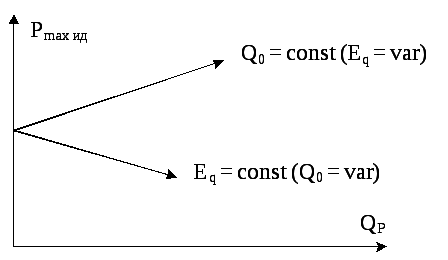
Рис. 3.8