Are there such deviations and, if so, what is their physical origin and interpretation?

–How can we describe and understand the “resonance peak” in INS experiments which reflects the interdependence of the elementary excitations and spin fluctuations? Does this provide information about the pairing interaction?

Another remarkable feature of the superconducting state of high–Tc cuprates is that they di er from conventional superconductors by having a small coherence length ξ. This length is usually associated with the average size of a Cooper pair, which for conventional superconductors is about 500

˚ 4 ˚

A–10 A. Therefore the size of a Cooper pair is larger than the average dis-

tance between pairs, resulting in a strong overlap of the corresponding wave

˚ functions. On the other hand, the cuprate superconductors have ξ 12 A–15

˚

A; these values have been obtained mainly from measurements of the upper critical field Hc2. All high–Tc cuprates are type II superconductors and are believed to be in the “clean limit” since the mean free path of the carriers

˚

( 150 A) is much larger than ξ. Note that the coherence length in the c

˚ ˚

direction ξc, is only 2 A–5 A, i.e. even smaller than the interplanar distance, while ξ in the planes is about three to four lattice spacings.

1.3 Triplet Pairing in Strontium Ruthenate (Sr2RuO4): Main Facts and Main Questions

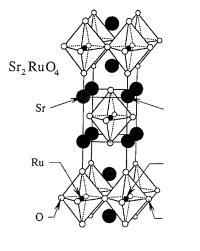
The discovery of high–Tc superconductivity in the cuprates led to extensive searches for other superconducting transition metal oxides. One important example is the novel superconductor strontium ruthenate (Sr2RuO4) which was discovered by Maeno and coworkers in 1994 [76]. Its crystal structure is isostructural to that of (La,Sr)2CuO4 (shown in Fig. 1.8), but it has Tc 1.5 K, and, more importantly, is believed to be a triplet superconductor. This makes a theoretical investigation of Sr2RuO4 very interesting.

The formal valence of the ruthenium ion is Ru4+, i.e. there are four remaining electrons within the 4d shell. Similarly to LSCO, the Ru ion sits at the center of a RuO6 octahedron, and the crystal field of the O2− ions splits the five 4d states into threefold t2g and fourfold eg subshells. The negative charge of O2− causes the t2g states to lie lower in energy, and the corresponding xy, xz, and yz orbitals form the Fermi surface. Owing to the large interplanar separation of the RuO6 octahedra, Sr2RuO4 has only a small energy dispersion along the c direction. Its highly planar structure leads also to very weak hybridization between xy orbitals and the xz and yz orbitals. Band structure calculations confirm these considerations and distribute the four electrons equally among all three orbitals [78]. The detailed shape of the Fermi surface has been determined from de Haas–van Alphen oscillations of

16 1 Introduction

Fig. 1.8. Structure of Sr2RuO4, which is similar to that of the high–Tc cuprate family La2−x Bax CuO4. However, its normal and superconducting properties are quite di erent from those of cuprates: they resemble more the properties of superfluid 3He, as described in the text. This is discussed in [77].

the magnetization in response to an external field and confirms the sheets of the Fermi surface predicted by band structure calculations.

Recent studies by means of INS [79] and nuclear magnetic resonance (NMR) [80] of the spin dynamics in Sr2RuO4 reveal the presence of strong incommensurate fluctuations in the RuO2 planes at the antiferromagnetic wave vector Qi = (2π/3, 2π/3). It was found from band structure calculations [81] that these fluctuations result from the nesting properties of the quasi-one- dimensional dxz and dyz bands. The two–dimensional dxy band contains only weak ferromagnetic fluctuations. In general, owing to spin–orbit coupling or hybridization, one expects strong spin fluctuations between the RuO2 planes in the z direction also [82, 83]. However, inelastic neutron scattering [84] shows that the magnetic fluctuations are purely two-dimensional and originate from the RuO2 planes. Both behaviors could result as a consequence of the magnetic anisotropy within the RuO2 planes as indeed was observed in recent NMR experiments by Ishida et al. [85]. In particular, by analyzing the temperature dependence of the nuclear spin–lattice relaxation rate for 17O in the RuO2 planes at low temperatures, these authors have demonstrated that the out–of–plane component of the spin susceptibility can become almost three times larger than the in–plane component. This strong and unexpected anisotropy disappears at approximately room temperature [85].

Superconductivity occurs in Sr2RuO4 only at low temperatures and in samples with a low residual resistivity, and it occurs out of a normal state that can be described well within Landau’s Fermi liquid theory. This is in contrast to high–Tc cuprates. On the other hand, one may argue that Tc 1.5 K is

a relatively large transition temperature because the superconducting Tc for triplet pairing in 3He is about 1 mK and thus three orders of magnitude smaller. An important result of Landau’s Fermi liquid theory is that the resistivity ρ at low temperatures T should follow a ρ T 2 law, which is a consequence of electron–electron collisions. The observation of this power law both within the RuO2 planes and perpendicular to them (but with di erent prefactors, of course) clearly indicates that Fermi liquid theory is applicable. Furthermore, measurements of the Fermi velocity by de Haas–van Alphen experiments show that the e ective mass is enhanced by a factor of 3 to 5, which agrees with values deduced from the specific heat coe cient, which is linear in T . This is also consistent with Landau’s Fermi liquid theory [77].

In short, many experiments have confirmed that the dominant interactions in Sr2RuO4 are electron–electron interactions rather than the weaker interactions of the electron–phonon kind. Thus, on general grounds, one would expect that the superconductivity would turn out to be unconventional. In general, owing to Pauli’s principle, (pairs of) fermions must have antisymmetric wave functions under particle interchange. For a Cooper pair this implies a relationship between the orbital and the spin character: orbital wave functions with even values for the orbital number (l = 0, 2, . . . ), as in cuprates, are even under particle interchange and thus are spin singlets; on the other hand, odd values (l = 1, 3, . . . ) require spin triplets. However, specifying the complete symmetry of the superconducting state requires more than just the angular–momentum channel and the spin state. The possible internal motion of the electrons (or holes) forming a Cooper pair has to be specified with respect to their center–of–mass coordinate, which must be in accordance with the underlying point group symmetry of the crystal. Note that the highly two-dimensional character of Sr2RuO4 (and its tetragonal symmetry) suggests pairing states that are mainly intraplanar rather than interplanar. This will be discussed later in detail.

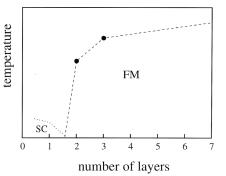
Finally, we would like to mention the main experimental evidence for spintriplet pairing in Sr2RuO4. The main proof comes from NMR experiments which measure the small change of the resonance line frequency caused by weak spin polarization of the electrons in an external applied field. In contrast to cuprates, where Cooper pairs are not polarized at all (because they are in a singlet state) and thus the Knight shift vanishes at low temperatures, in Sr2RuO4 no change (within the ab plane) has been observed [87]. This is expected for a triplet superconductor with parallel spins, where the application of a magnetic field changes only the relative numbers of spins parallel and antiparallel to the field. Thus the Knight shift is unchanged from its value in the normal state. Of course, these conclusions are only true for small spin– orbit coupling, i.e. L · S coupling, which seems to be the case for Sr2RuO4. More evidence for triplet pairing comes from the fact that the phase diagram of the Ruddlesen–Popper series (Fig. 1.9) suggests that Sr2RuO4 is indeed in the vicinity of a ferromagnetic transition. This, in analogy to 3He, should

18 1 Introduction

Fig. 1.9. Schematic phase diagram T (n) of the Ruddlesen–Popper series Srn+1Run O3n+1 (after Sigrist et al. [86]). The number of layers is the parameter that determines the transition from a superconducting (SC) to a ferromagnetic (FM) state.

lead to a triplet state due to parallel spins already present in the normal state, and to p–wave pairing [45]. However, by fitting the specific heat and the ultrasound attenuation, Dahm et al. found reason to doubt the presence of p–wave superconductivity [88] and have proposed an f –wave symmetry of the superconducting order parameter. A similar conclusion has been drawn in [89]. Recently it has been reported that thermal–conductivity measurements are also most consistent with f –wave symmetry or with p–wave pairing within the planes and with nodes between the planes [90]. We shall therefore discuss later why the simple picture of p–wave pairing has to be modified strongly.

To summarize, the main questions in connection with Cooper pairing in Sr2RuO4 are:

–How can we explain the elementary excitations in the normal state, in particular the strong magnetic anisotropy observed in NMR experiments? What is the role of spin–orbit coupling and hybridization between the bands?

–How can we formulate an electronic theory for Cooper pairing in triplet superconductors, taking into account an interplay between ferromagnetic and strong antiferromagnetic spin fluctuations (resulting from nesting properties)?

–What symmetry of the superconducting order parameter is present in Sr2RuO4, if Cooper pairing due to spin excitations occurs mainly in–plane or mainly between RuO2 planes?