
- •Preface
- •Contents
- •1 Introduction
- •Layered Materials and Their Electronic Structure
- •General Phase Diagram of Cuprates and Main Questions
- •Superconducting State: Symmetry of the Order Parameter
- •Triplet Pairing in Strontium Ruthenate (Sr2RuO4): Main Facts and Main Questions
- •From the Crystal Structure to Electronic Properties
- •Spin Fluctuation Mechanism for Superconductivity
- •References
- •Generalized Eliashberg Equations for Cuprates and Strontium Ruthenate
- •Theory for Underdoped Cuprates
- •Extensions for the Inclusion of a d-Wave Pseudogap
- •Derivation of Important Formulae and Quantities
- •Elementary Excitations
- •Raman Scattering Intensity Including Vertex Corrections
- •Optical Conductivity
- •Comparison with Similar Approaches for Cuprates
- •The Spin Bag Mechanism
- •Other Scenarios for Cuprates: Doping a Mott Insulator
- •Local vs. Nonlocal Correlations
- •The Large-U Limit
- •Projected Trial Wave Functions and the RVB Picture
- •Current Research and Discussion
- •References
- •The Spectral Density Observed by ARPES: Explanation of the Kink Feature
- •Raman Response and its Relation to the Anisotropy and Temperature Dependence of the Scattering Rate
- •A Reinvestigation of Inelastic Neutron Scattering
- •Collective Modes in Electronic Raman Scattering?
- •Elementary Excitations and the Phase Diagram
- •Optical Conductivity and Electronic Raman Response
- •Brief Summary of the Consequences of the Pseudogap
- •References
- •4 Results for Sr2RuO4
- •Elementary Spin Excitations in the Normal State of Sr2RuO4
- •The Role of Hybridization
- •Comparison with Experiment
- •Symmetry Analysis of the Superconducting Order Parameter
- •Triplet Pairing Arising from Spin Excitations
- •Summary, Comparison with Cuprates, and Outlook
- •References
- •5 Summary, Conclusions, and Critical remarks
- •References
- •References
- •Index
208 5 Summary, Conclusions, and Critical remarks
between the RuO2 planes. The exact position of the nodes reflects the incommensurability of the pairing interaction. This has to be confirmed by an electronic, self-consistent calculation.
What are the weak points of our theory? As we have discussed in Sect. 2.5, the main problem of our approach is the fact that when the doping x tends to zero no Mott transition is obtained. Therefore, as soon as the nearness of a Mott transition becomes important, i.e. in the (strongly) underdoped regime, our theory has problems. For optimal doping and the overdoped case, however, we believe that our results demonstrate that the physics related to a Mott–Hubbard insulator plays no dominant role, and hence can safely be neglected. In particular, our approximation is better for Sr2RuO4, which is a material with weaker correlations than in cuprates and is also a good Fermi liquid.
Further weak points are the following: for cuprates we have used only an e ective one-band Hubbard model that neglects the di erence between oxygen p states and Cu d states. In addition, we have employed a simple perturbation theory (e ectively second order) and the RPA, and thus consider only a special selection of Feynman diagrams. The corresponding vertex corrections can often be treated only within certain approximations. In defence of our work, however, we believe we have followed an intuitive method and formulated a theory similar to the well-known Eliashberg equations for phonons given by Scalapino, Schrie er, and Wilkins [11], yielding fair agreement with experiment.
To conclude, we have studied the interplay between magnetism and superconductivity, in particular the connection between antiferromagnetism and singlet d-wave superconductivity in high-Tc cuprates, and between ferromagnetism and triplet pairing in Sr2RuO4. We have developed an electronic theory of Cooper pairing due to spin fluctuations and understood the main physics in these materials. However, in connection with cuprates many questions still have to be answered. For example, what is the role of spatial [12] or electronic [13] inhomogeneities, do surface properties di er strongly from their bulk counterparts ([14] and references therein), and how should one interpret the recent c-axis tunneling data [15]? We believe that further materialdependent studies are necessary to clarify these questions [16]. Nevertheless, many fingerprints of the corresponding pairing potential due to spin excitations are found in various normal and superconducting properties. Because the doping dependence of the key physical quantities and the elementary excitations are correctly described, we conclude that spin fluctuations play the most important role in Cooper pairing in these materials.
References
1.B. Stadlober, G. Krug. R. Nemetschek, R. Hackl, J. L. Cobb, and J. T. Markert, Phys. Rev. Lett. 74, 4911 (1995). 201
References 209
2.L. Al , A. Beck, R. Gross, A. Marx, S. Kleefisch, T. Bauch, H. Sato, M. Naito, and G. Koren, Phys. Rev. B. 58, 11197 (1998). 201
3.S. M. Anlage, D.-H. Wu, S. N. Mao, X. X. Xi, T. Venkatesan, J. L. Peng, and
R.L. Greene, Phys. Rev. B. 50, 523 (1994). 201
4.C. C. Tsuei and J. R. Kirtly, Phys. Rev. Lett. 85, 182 (2000). 201
5.J. D. Kokales, P. Fournier, L. V. Mercaldo, V. V. Talanov, R. L. Greene, and
S.M. Anlage, Phys. Rev. Lett. 85, 3696 (2000). 201
6.R. Prozorov, R. W. Gianetta, P. Furnier, and R. L. Greene, Phys. Rev. Lett. 85, 3700 (2001). 201
7.N. P. Armitage, D. H. Lu, D. L. Feng, C. Kim, A. Damascelli, K. M. Shen, F. Ronning, Z. X. Shen, Y. Onose, Y. Taguchi, and Y. Tokura, Phys. Rev. Lett. 86, 1126 (2001). 201
8.T. Sato, T. Kamiyama, T. Takahashi, K. Kurahashi, K. Yamada, Science 291, 1517 (2001). 201
9.A. Lanzara, P. V. Bagdanov, X. J. Zhou, S. A. Kellar, D. L. Feng, E. D. Lu,
H.Eisaki, A. Fujimori, K. Kishio, J.-I. Shimoyama, T. Noda, S. Uchida, Z. Hussain, and Z. X. Shen, Nature 412, 510 (2001). 204
10.R. Zeyher and A. Greco, Phys. Rev. Lett. 89, 177004 (2002). 206
11.D. J. Scalapino, J. R. Schrie er, and J. W. Wilkins, Phys. Rev. 148, 263 (1966). 208
12.K. M. Lang, V. Madhavan, J. E. Ho man, E. W. Hudson, H. Eisaki, S. Uchida, and J. C. Davis, Nature 415, 412 (2002). 208
13.S. H. Pan, J. P. O’Neal, R. L. Badzey, C. Chamon, H. Ding, J. R. Engelbrecht,
Z.Wang, H. Eisaki, S. Uchida, A. K. Gupta, K.-W. Ng, E. W. Hudson, K. M. Lang, and J. C. Davis, Nature 413, 282 (2001). 208
14.K. A. M¨uller, Phil. Mag. Lett. 82, 279 (2002). 208
15.R. A. Klemm, Physica B 329–333, 1325 (2003). 208
16.J. Bobro , H. Alloul, S. Quazi, P. Mendels, A. Mahajan, N. Blanchard, G. Collin, V. Guillen, and J.-F. Marucco, Phys. Rev. Lett. 89, 157002 (2002). 208
A Solution Method
for the Generalized Eliashberg Equations for Cuprates
While earlier attempts were restricted to solving the set of equations (2.28)– (2.32) on the imaginary axis [1, 2, 3, 4] or slightly above the real axis [5, 6, 7], we solve the generalized Eliashberg equations directly on the real ω axis. Thus we avoid continuation methods such as the Pad´e approximation after solving the set of equations for the self-energy. The generalized Eliashberg equations in the two-dimensional (e ective) one-band Hubbard model read
Im χG(q, ω) = |
|
|
π |
|
k |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
N |
|
−∞ dω [f (ω) − f (ω + Ω)] N (k, ω)N (k + q, ω + Ω) , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(A.1) |
||
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im χF (q, ω) = |
|
π |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
N |
|
−∞ dω [f (ω) − f (ω + Ω)] A1(k, ω)A1(k + q, ω + Ω) , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(A.2) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
∞ |
|
|
|
Im χG,F (q, ω) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Re χG,F (q, ω) = |
|
|
P |
−∞ dω |
|
|
|
, |
(A.3) |
|||||||||||||||||||
|
π |
|
|
ω − Ω |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
χc0 = χG − χF |
, |
|
|
|
|
(A.4) |
||||||||||||||
|
|
|
|
|
|
|
|
|
χs0 = χG + χF |
, |
|
|
|
|
(A.5) |
||||||||||||||
|
|
|
|
|
|
|
|
Ps ≡ |
1 |
Im |
3 U 2χs0 |
|
, |
|
(A.6) |
||||||||||||||
|
|
|
|
|
|
|
|
|
π |
2 |
|
1 − U χs0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
Pc ≡ |
1 |
Im |
3 U 2χc0 |
|
, |
|
(A.7) |
||||||||||||||
|
|
|
|
|
|
|
|
|
π |
2 |
|
1 + U χc0 |
|
|
|||||||||||||||
|
|
|
|
PG |
≡ Ps + Pc − π Im |
2 U 2 |
(χs0 + χc0) |
, |
(A.8) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
PF ≡ −Ps + Pc |
+ π |
Im |
2 U 2 (χs0 − χc0) |
, |
(A.9) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
π |
|
|
|
q |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im φ(k, ω) = N |
−∞ dΩ [b(Ω) + f (Ω − ω)] PF (q, ω)A1(k − q, ω − Ω) , |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(A.10) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D. Manske: Theory of Unconventional Superconductors, STMP 202, 211–228 (2004)c Springer-Verlag Berlin Heidelberg 2004
212 A Solution Method for the Generalized Eliashberg Equations for Cuprates
Im Σ(k, ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
π |
q |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= −N |
−∞ dΩ [b(Ω) + f (Ω − ω)] PG(q, ω)N (k − q, ω − Ω) , (A.11) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∞ |
|
Im φ(k, ω |
) |
|
|
|
|
|
|
|
|
|
|
Re φ(k, ω) = |
|
P |
−∞ dω |
|
|
|
|
, |
(A.12) |
||||||||||
|
|
|
π |
|
ω − ω |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∞ |
|
Im ΣG(k, ω |
) |
|
|
|||
|
|
|
Re ΣG(k, ω) = |
|
P |
−∞ dω |
|
|
|
|
, |
(A.13) |
||||||||||||
|
|
|
π |
|
ω − ω |
|
|
|
||||||||||||||||
|
|
|
|
|
ξ ≡ |
1 |
ΣG(k, ω) + ΣG (k, −ω) |
, |
|
|
(A.14) |
|||||||||||||
|
|
|
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
ΣG(k, ω) |
− ΣG (k, −ω) |
|
|
(A.15) |
|||||||||||
|
|
|
|
ωZ ≡ ω − |
|
|
|
, |
||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||
N (k, ω) = −π Im (ωZ)2 − ( k |
+ ξ)2 |
− φ2 = A0(k, ω) + A3(k, ω) , |
||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
ωZ + k + ξ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
A1(k, ω) = −π Im (ωZ)2 |
− ( k + ξ)2 − φ2 |
. |
(A.16) |
||||||||||||||||||
|
|
|
(A.17) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
φ |
|
|
|
|
|
|||
Our numerical calculations were performed on a square lattice with 256 ×256 points in the Brillouin zone and with 200 points on the real ω axis up to 16t with an almost logarithmic mesh. The full momentum and frequency dependence of the quantities was kept. The convolutions in k-space were carried out with fast Fourier transforms [8]. The real parts of the susceptibilities, gap, and self-energy were calculated with the help of the Kramers–Kronig relations (P denotes the corresponding principal value of the integral). The spectral functions A1, PG,F , Im φ, Im ξ, and Im χG,F are antisymmetric and the corresponding real parts are symmetric with respect to ω. Thus the spectral function for the interacting electrons (or holes) N (k, ω) is separated into a symmetric part A0 and an antisymmetric part A3 (see (A.16)). The corresponding equations for the normal state can be recovered by setting the o -diagonal terms of the self-energy, φ, A1, and χF , identically to zero.
For an illustration, we show in Fig. A.1 how we solve (2.28)–(2.32). We start with a dynamical spin susceptibility χ(q, ω) and constructs the e ective pairing interaction using (A.8). Then, the strong-coupling gap equation for the superconducting order parameter φ(k, ω) and the corresponding Dyson equation G−1(k, ω) = G−0 1(k, ω) − Σ(k, ω) have to be solved. Having solved these two equations, we have new appropriate starting input values for an electron propagator G, which is again used to calculate χ. This procedure is repeated until all equations are solved.
In order to determine the superconducting transition temperature Tc we solve the linearized gap equation, i.e. the linearized version of (A.12),
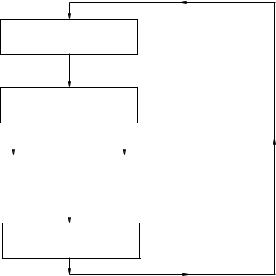
A Solution Method for the Generalized Eliashberg Equations for Cuprates |
213 |
dynamical spin susceptibility
pairing interaction
|
|
|
|
|
|
|
|
|
|
|
|
|
gap equation |
|
|
|
self energy |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
electron propagator
Fig. A.1. Illustration of the procedure used to solve (2.28)–(2.32). The full momentum and frequency dependence of the quantities is kept. Thus, our calculations include pair-breaking e ects for the Cooper pairs resulting from lifetime e ects of the elementary excitations.
1 |
|
|
∞ |
|
|
|
λ Im φ(k, ω) = −N k |
−∞ dω [b(Ω) + f (Ω − ω)] PF (q, ω) |
|
||||
|
|
|
|
|
|
|
|
|
|
φ(k , ω ) |
|
(A.18) |
|
× Im |
(ωZ)2 − ( k + ξ)2 |
, |
||||
where χF in PF is set identically to zero. With decreasing temperature T , the eigenvalue λ(T ) increases and passes through unity at T = Tc. The spectral functions calculated during the solution of (A.18) are then appropriate starting values for the solution of the equations below Tc. After solving the generalized Eliashberg equations for cuprates, we find that below Tc the superconducting gap function has dx2−y2 -wave symmetry for both holeand electron-doped superconductors. Vertex corrections for the two-particle correlation function are not included.
As mentioned earlier, there exists an important feedback e ect of the selfenergy on the spectral functions of the corresponding quasiparticles (dressed holes or electrons). This is the case, in particular if these quasiparticles become superconducting. Below Tc a gap appears in the spectral density of the quasiparticles which not only condense into Cooper pairs but also provide the e ective pairing interaction V ef f (q, ω). This gap corresponds to the superconducting gap function φ(k, ω) = Z(k, ω)∆(k, ω), which is nonzero below Tc
