This Introduction is organized as follows: first, we present the most relevant materials, and their crystal and electronic structures. Then, in Sect. 1.2, we ask the most important questions in connection with the phase diagram and the elementary excitations of cuprate high–Tc superconductors, which will be answered in Chap. 3. In Sect. 1.3, we introduce Sr2RuO4. In Sect. 1.4, we describe how to find an appropriate Hamiltonian for both cuprates and ruthenates and give some general arguments about the expected symmetry of the superconducting order parameter.

1.1 Layered Materials and Their Electronic Structure

Before deriving an electronic theory for Cooper pairing in cuprates, one has to analyze and understand the underlying crystal structure and corresponding electronic properties. In general, all high–Tc cuprates are basically tetragonal

˚

with a lattice constant of about 3.8 A and consist of one or more CuO2 planes in their structure, which are separated by layers of other atoms (Ba, La, O,

˚

. . . ). The in–plane oxygen bond length is about 1.9 A. As mentioned above, most researchers in this field believe that superconductivity is related to processes occurring in the CuO2 planes, whereas the other layers simply provide the carriers. All cuprates have such charge reservoirs. The superconducting transition temperature Tc seems to depend on the number of CuO2 planes per unit cell; for example, the three–layer Hg and Tl compounds have a Tc of 134 K and 127 K, respectively. The fact that Tc increases with the number of layers has led to speculation about increasing Tc up to room temperature which, however, has not been not realized up to now [6].

In Tables 1.1and 1.2, we present some materials and their corresponding Tc. For comparison, we also list some “cold” superconductors such as the heavy–fermion compound UPt3, the BCS–Eliashberg–like superconductors Nb and Pb, and Nb3Ge, which had the highest Tc before the discovery of cuprates by Bednorz and M¨uller in 1986 [7].

We present also the recently discovered (phonon-induced) “high–Tc” superconductor MgB2 and the C60 compounds. Very recently it has been demonstrated that even iron becomes superconducting at Tc 2 K, but

Table 1.1. Superconducting transition temperatures of cuprate materials.

HgBa2Ca2Cu3O8+δ 134

Tl2Ca2Ba2Cu3O10 127

YBa2Cu3O7 92

Bi2Sr2CaCu2O8 89

La1.85Sr0.15CuO4 39

41 Introduction

Table 1.2. Superconducting transition temperatures of some “cold” superconductors, of Sr2RuO4, and of other compounds.

only in its nonmagnetic phase, i.e. when high pressure is applied [8]. For a more complete list of superconducting materials, see [9, 10].

It is well established that the so–called undoped parent cuprate compounds are insulators and that their Cu spins are ordered antiferromagnetically below a N´eel temperature TN . However, this contradicts a simple bandstructure point of view. For example, the formal valencies of La3+, O2−, and Cu2+ in the parent compound La2SrCuO4 lead to an [Ar] 3d9 state, which contains a single d–hole located within the planar 3dx2−y2 orbital. Thus, a naive argument would suggest that the undoped parent compounds are simple metals, which was also concluded from by early local–density approximation (LDA) calculations. This is not restricted to La2SrCuO4; in fact, the LDA behaves similarly for other parent compounds. As we shall discuss later, the inconsistency of LDA calculations is a direct consequence of an improper treatment of the strong local Coulomb correlations. On the other hand, it is obvious that the localized copper spins provide the magnetic moments for the antiferromagnetic order. The in–plane exchange coupling J|| is generated by Cu-spin superexchange and can be well described by a two-dimensional spin–1/2 Heisenberg model. Inelastic neutron scattering (INS) experiments [11, 12] and Raman scattering [13] have measured J|| 100 meV and a large anisotropy with respect to the next unit cell, J /J|| 10−5 [14, 15]. Therefore, above TN , the spin correlations are essentially two–dimensional.

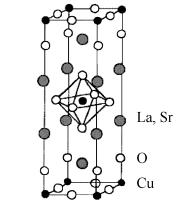
1.1.1 La2−xSrxCuO4

This compound, usually abbreviated to LSCO, crystallizes in a body–centered tetragonal structure (similar to K2NiF4) and is shown in Fig. 1.1. The CuO2

˚

planes are approximately 6.6 A are apart and separated by two LaO planes, which form the charge reservoir. Each copper atom in the conducting planes has a bond to oxygen atoms above and below in the c direction, which are

Fig. 1.1. Structure of the hole-doped high-Tc cuprate La2−x Srx CuO2 (LSCO), which has a perovskite-like structure with one CuO2 plane per unit cell. It is believed that the main physics related to Cooper-pairing occurs within the CuO2 planes.

called apical oxygens. This is typical for all hole–doped high–Tc cuprate materials. Furthermore, the Cu ions are surrounded by octahedra of oxygens as in a perovskite structure. The Cu–O bond in the c direction is much weaker

˚

than in the ab plane because its length is considerably larger ( 2.4 A) than

˚

the Cu–O distance in the CuO2 planes ( 1.9 A). Thus the dominant bonds are those in the planes, and the importance of the apical oxygens is still under discussion.

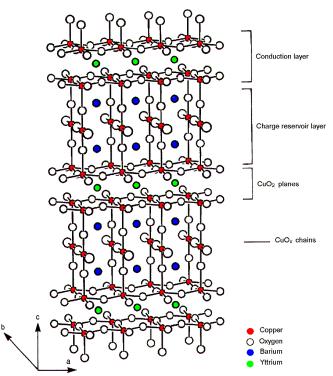
1.1.2 YBa2Cu3O6+x

˚

In YBCO, there are two CuO2 planes per unit cell, approximately 3.2 A apart and separated by yttrium ions. The tetragonal structure of this compound is shown in Fig. 1.2. The pairs of CuO2 planes are themselves separated by atoms of barium, oxygen, and copper forming the charge reservoir. The dis-

˚

tance between adjacent pairs of these conducting planes is 8.2 A. As is the case for LSCO, the number of carriers in the CuO2 planes is controlled by the amount of charge transferred between the conducting layers and charge reservoir layers. Note that in YBCO there are Cu atoms in the charge reservoir, in contrast to LSCO. In combination with oxygen, they form Cu–O chains along the b direction, which leads to an orthorhombic distortion. The

˚

Cu–O distance is about 1.9 A, as in the planes. For YBa2Cu3O7, i.e. x = 1, the chains are well defined, but they are absent for the undoped parent compound YBa2Cu3O6. It is usually believed that adding oxygen to the chains is equivalent to adding holes to the CuO2 planes. For more details, see [9]. Because of the nonlinear increase of the in–plane hole density with the doping x, YBCO has a so–called 60 K plateau in its Tc(x) curve, which will be discussed later.

61 Introduction

Fig. 1.2. Structure of the hole–doped high–Tc superconductor YBa2Cu3O6+x (YBCO). It consists of two CuO2 planes per unit cell and charge reservoirs. In contrast to LSCO, YBCO has Cu–O chains, which are formed along the b direction.

1.1.3 Nd2−xCexCuO4

The structure of this compound, usually abbreviated to NCCO, is body– centered tetragonal like LSCO and is shown in Fig. 1.3. The di erence between NCCO and LSCO lies in the position of the oxygen atoms of the charge reservoir. It is interesting to note that LSCO can be easily doped with holes, while NCCO can be easily doped with electrons. In the NCCO crystal, copper becomes Cu2+, oxygen becomes O2−, and neodymium is in the Nd3+ state. After doping with Ce4+, which replaces Nd ions, the CuO2 planes gain an excess of electrons. It is believed that an additional electron occupies a hole of the d shell of Cu (producing a closed–shell configuration) and does not move to an oxygen site as is the case for hole–doped cuprates. Thus, di erent bands are doped by holes and electrons, and one expects, on general grounds, that the phase diagram of hole– and electron–doped cuprates will not be symmetric with respect to the carrier concentration x.