
Dressel.Gruner.Electrodynamics of Solids.2003
.pdf
328 |
12 Metals |
parameters, an effective coupling constant
λP = 2 |
|
dωP |
αP2 F(ωP) |
(12.2.12) |
ωP |
can be defined; needless to say, αP can also be frequency dependent. The initial state is a photon of energy h¯ ω, and the final state involves an electron and hole with energies E1 and E2, respectively, and a phonon with energy h¯ ωP. If we assume that the matrix element is independent of frequency (except for the factor ω−1/2 representing the photon state), the transition probability, and thus the absorptivity A, is given as
A(ω) |
1 |
|
dE1dE2dωP De(E1)Dh(E2) αP2 (ωP) F(ωP) δ{E1 + E2 + h¯ ωP − h¯ ω} , |
ω |
(12.2.13) where De(E1) and Dh(E2) are the density of electrons and holes, respectively, A(ω) can be written as
1 |
ω |
|
A(ω) ω 0 |
(ω − ωP)αP2 F(ωP) dωP |
(12.2.14) |
at zero temperature. For a narrow density of phonon states centered around ωP0 , A(ω) has a structure at ω = ωP0 ; in general, the frequency dependence of the absorption reflects the phonon density of states.
This absorptivity can be cast into a form we used earlier, by assuming a frequency dependent relaxation rate 1/τ (ω) and renormalized plasma frequency [All71]. In the relaxation regime ωτ 1 and ω ωp – in the infrared spectral range for typical metals – the absorptivity is, according to Eq. (5.1.22),
A = |
2 |
; |
|
||
ωpτ |
and therefore we can define a frequency dependent relaxation rate
1 |
|
2π |
0 |
ω |
|
|
≈ |
|
(ω − ωP) αP2 F(ωP) dωP . |
(12.2.15) |
|
τ (ω) |
ω |
This scattering time depends on the structure factor αP2 F(ωP); the phonon limited scattering rate 1/τ approaches zero at low frequencies, while at high frequencies it saturates at
1 |
= π λP ωP , |
(12.2.16) |
τ |
where ωP is the average phonon frequency weighted by the effective coupling constant λP we have defined in Eq. (12.2.12). Of course, having just a frequency dependent scattering rate violates the Kramers–Kronig relations; it has to be accompanied by a frequency dependent mass, which can be established along similar

12.2 Effects of interactions and disorder |
329 |
lines to the introduction of the frequency parameter into the Drude model earlier (Eqs (12.2.1)–(12.2.5)).
From the absorptivity A(ω) the optical parameters 1/τ (ω) and λP(ω) can be extracted, and eventually the weight factor α2 F(ωP) can be derived. Although this works in principle, in practice F(ωP) is modeled by, for instance, harmonic oscillators. The structure thus obtained should be related to F(ωP) as evaluated from inelastic neutron scattering, and in cases where the analysis has been performed, this is indeed the case [Joy70, McK79].
Because of the Bose statistics of the relevant phonon modes, this renormalization is also temperature dependent. As before for electron–electron interactions, the frequency and temperature dependent relaxation rates go hand in hand (but because of the Bose–Einstein population factor the functional forms are somewhat different), and the zero temperature scattering rate, as given by Eq. (12.2.15), has its temperature dependent counterpart. One finds that
1 |
|
= |
0 |
∞ |
hω |
|
|
|
hω |
|
|
τ (T, ω = 0) |
|
kBT |
2¯kBT |
||||||||
|
|
|
π |
dωP |
¯ |
P |
sin2 |
|
|
P |
α2(ωP) F(ωP) , (12.2.17) |
|
|
|
|
|
|
||||||
and this parameter can be extracted in principle from the temperature dependent dc conductivity.
12.2.3 Strongly disordered metals
Throughout the previous discussion of the experiments, we have assumed that the electron states are delocalized, and furthermore that they can be represented as plane waves or Bloch functions; this clearly holds for pure metals in the absence of disorder. For a small amount of disorder, or for a small amount of impurities in the sample, we expect that the effects of disorder and impurities are absorbed into the relaxation rate, with impurity scattering assumed to lead to an extra contribution to 1/τ . This is, furthermore, usually assumed to be independent of other scattering mechanisms, leading to the (experimentally well confirmed) Matthiessen rule in the case of dc conduction. This picture then also implies that the Drude model still applies, with a modified relaxation rate. Consequently we expect a reduced dc conductivity and a Drude roll-off which now occurs at higher frequencies. The total spectral weight associated with the conductivity and thus the plasma frequency is, however, determined only by the number of carriers and by their bandmass; consequently it remains little changed. The situation is different for strong disorder effects. It was shown by Anderson in a classic paper [And58] that for a sufficient amount of disorder all states are localized, and therefore by increasing disorder there is a transition from delocalized electron states to states with the absence of diffusion, hence to a state where all electrons are localized. In
330 |
12 Metals |
three dimensions, the condition for this is given by V / W , where V is the overall, average strength of the random potential and W is the single-particle bandwidth. In a one-dimensional electron gas, in contrast, all states are localized for any small disorder [Blo72, Mot61]. The consequences of localization are profound: the dc conductivity is zero at T = 0, and we have an insulator; at finite temperatures, conduction proceeds by mechanisms which are fundamentally different from those which determine the resistivity of conventional metals. We cannot do justice to the field, which goes by the names of Anderson transition or localization driven metal–insulator transition, within the limitations of this book, and therefore we simply recall the various expressions, first for the temperature dependence of the dc conductivity, which have been proposed and found, and later for the frequency dependent transport.
Right at the metal–insulator transition, scaling arguments prevail [Bel94], and they can be used to establish the temperature dependence of the conductivity. Such arguments give a power law dependence:
σdc(T ) = AT α ; |
(12.2.18) |
for a non-interacting electron gas, α = 1/3, for example. On the metallic side, and also on the insulating side except at rather low temperatures (or frequencies, as we will see later), the conductivity is finite at zero temperature, and the magnitude goes smoothly to zero upon approaching the transition. The temperature dependent dc conductivity is then described using the form
σdc(T ) = AT α + B |
(12.2.19) |
where the factor A is independent and the factor B is dependent on the parameter x which controls the transition (usually concentration of scattering centers, the pressure, or the magnetic field). The residual conductivity B goes to zero as the transition is approached from both sides:
B(x) (x − xc)µ , |
(12.2.20) |
where xc is the critical parameter where the metal–insulator transition occurs and µ is the characteristic exponent. In the insulating state, Eq. (12.2.19) still describes the conductivity if B is negative. At low temperatures, well in the localized regime (called the Fermi glass regime), such scaling arguments do not apply and a different picture emerges. Here thermally assisted hopping between localized states which lie within the energy range kBT at temperature T determines the dc transport properties. The spatial proximity of such states depends on the temperature, hence the hopping is of variable range, and the evaluation of the most probable hop leads
12.2 Effects of interactions and disorder |
331 |
|||
to [Mot68, Mot69] |
|
|
|
|
σdc(T ) exp − |
T |
|
β |
|
0 |
, |
(12.2.21) |
||
T |
||||
where the exponent β = 1/(d + 1) is a function of the dimensionality d; for three dimensions β = 1/4, and it is 1/2 for the one-dimensional variable range hopping regime [Mot68]. The characteristic temperature T0 depends on the spatial extension of the localized states, the localization length λ0, and also on the density of states at the Fermi level D(EF); the localization length diverges as we approach the transition from the localized side. As the temperature rises, a crossover from this variable range hopping regime to the scaling regime occurs; the crossover temperature where this happens increases as the disorder becomes stronger, and we move away from the transition. Electron–electron interactions, in concert with disorder, modify this picture since such interactions depress the density of states (leading to a so-called Coulomb gap) at the Fermi energy, and consequently the power laws which determine the behavior at the transition. At the strongly localized regime, which is often referred to as a Coulomb glass, both exponents are modified; in Eq. (12.2.18) α = 1/3 for non-interacting electrons, α = 1/2 for strong electron–electron interactions [Efr75], and β in Eq. (12.2.21) changes from 1/4 to 1/2 in three dimensions [Efr75]. All this is well confirmed by temperature dependent transport measurements [All93, Her83] on various model systems, such as Nbx Si1−x where the metal–insulator transition occurs with decreasing x, or for phosphorus doped silicon Si:P [Loh98, Ros81] for which the impurity states, introduced by the doping, become delocalized by increasing their concentration.
Next we turn to the frequency dependent response, at temperatures low enough such that the condition h¯ ω kBT applies; not surprisingly, we find a close correspondence between the temperature and frequency dependences predicted, and in some cases also observed. Because of localization, the conductivity vanishes at zero frequency (at zero temperature) on the insulating side, and the frequency dependence is determined by transitions between localized states induced by the applied electromagnetic field. At low frequencies the conductivity therefore increases as ω rises, but at sufficiently high frequencies a Drude roll-off is still expected as inertia effects become important there. The well known sum rule
|
|
ω2 |
σ1(ω) dω = |
p |
|
8 |
still applies, as excitations from localized states are also possible and contribute to the spectral weight; interband transitions, of course, can influence this argument. The frequency dependence of the conductivity is shown in Fig. 12.15, for materials right at and at both sides of the metal–insulator transition. Starting from a weakly
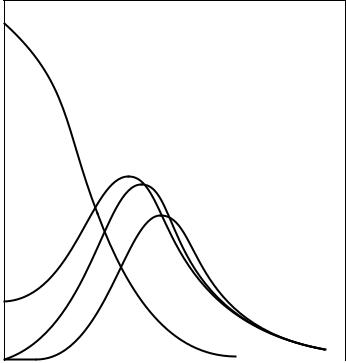
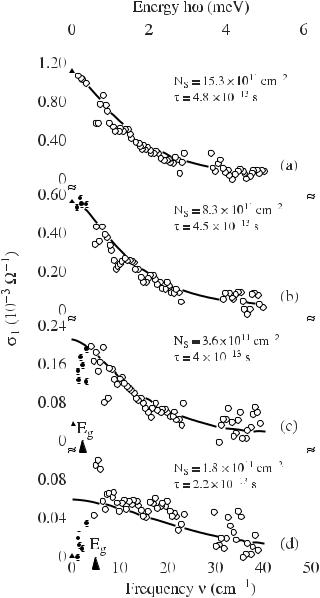

334 |
12 Metals |
low frequencies because the low spectral range of interest is difficult to explore at low temperature. There is an abundance of theoretical predictions on how the conductivity should depend on frequency, along the lines of what is predicted for the temperature dependence of the dc conductivity. Close to the transition (and also on the localized side of the transition at rather low frequencies) the conductivity at a temperature T → 0 should follow the power law
σ1(ω) = A ωα ± B |
(12.2.22) |
with the positive sign appropriate for the metallic side and the negative sign for the insulating side (obviously not at too low temperatures). The parameters depend upon the importance of electron–electron interactions [Lee85, Vol82] just like in Eq. (12.2.19) for σdc(T ). If electron–electron interactions are important, the exponent α is the same as that for the temperature dependent dc conductivity. Deep in the localized regime, arguments similar to those which were developed for variable range hopping lead to the conductivity
|
|
λ05 |
|
hω |
4 |
||
|
|
||||||
σ1(ω) |
|
D(EF) |
ω2 |
ln |
|
I0 |
(12.2.23) |
|
|
¯ |
|||||
|
|
|
|
|
|
||
in three dimensions. Again, λ0 is the localization length, D(EF) is the density of states at the Fermi level, and I0 denotes a parameter which determines the overlap integral of localized states and depends exponentially on λ0. The above expression is close to an ω2 functional form. Just as in the case of variable range dc hopping, electron–electron interactions modify this equation, and the leading term of the frequency dependence is
|
|
I0 |
4 |
|
|
σ1 |
(ω) ω ln |
. |
(12.2.24) |
||
hω |
|||||
|
¯ |
|
|
||
Similar to the temperature dependence, there is a smooth crossover to a power law frequency dependence, described by Eq. (12.2.22) with increasing frequencies; we can define a crossover frequency which is related to the crossover temperature mentioned above. These frequency dependences are indicated in Fig. 12.15.
From the above a close correspondence is expected between the temperature dependence (for kT h¯ ω) and the frequency dependence (for kT h¯ ω) of the conductivity at low energy scales, well below the frequencies where a crossover to the Drude roll-off occurs, or temperatures where other scattering processes or thermal excitations play a role. In Fig. 12.17 we display the temperature (at ω → 0) and frequency dependence (at low temperature for which kT h¯ ω applies) for amorphous Nbx Si1−x in the vicinity of the metal–insulator transition. There is a close correspondence between the temperature and frequency dependent conductivity in all three cases; the temperature and frequency dependencies can be
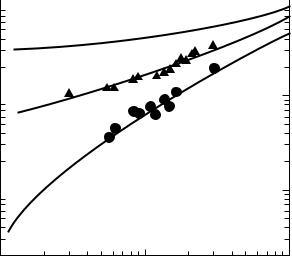
336 |
12 Metals |
increase of the correlation length as the transition is approached. Such behavior has been observed in Si:P [Ros81, Gay95].
References
[Abe66] F. Abeles,` ed., Optical Properties and Electronic Structure of Metals and Alloys
(North-Holland, Amsterdam, 1966)
[All71] |
P.B. Allen, Phys. Rev. B 3, 305 (1971) |
[All75] |
S.I. Allen, D.C. Tsui, and F.D. Rosa, Phys. Rev. Lett. 35, 1359 (1975) |
[All93] |
S.I. Allen, M.H. Paalanen, and R.N. Bhatt, Europhys. Lett. 21, 927 (1993) |
[Alt85] |
B.L. Altschuler and A.G. Aronov, in: Electron–Electron Interaction in |
|
Disordered Systems, edited by A.L. Efros and M. Pollak (North-Holland, |
|
Amsterdam, 1985) |
[And58] P.W. Anderson, Phys. Rev. 109, 1492 (1958)
[And61] P.W. Anderson, Phys. Rev. 124, 41 (1961)
[Ash76] N.W. Ashcroft and N.D. Mermin, Solid State Physics (Holt, Rinehart and Winston, New York, 1976)
[Awa93] A.M. Awasthi, L. Degiorgi, G. Gruner,¨ Y. Dalichaouch, and M.B. Maple, Phys. Rev. B 48, 10 692 (1993)
[Bel94] D. Belik and T.R. Kirkpatrick, Rev. Mod. Phys. 66, 261 (1994)
[Ben66] H.E. Bennett and J.M. Bennett, Validity of the Drude Theory for Silver, Gold and Aluminum in the Infrared, in: Optical Properties and Electronic Structure of Metals and Alloys, edited by F. Abeles` (North-Holland, Amsterdam, 1966)
[Blo72] A.N. Bloch, R.B. Weismon, and C.M. Varma, Phys. Rev. Lett. 28, 753 (1972)
[Cha52] R.G. Chambers, Proc. Phys. Soc. (London) A 65, 458 (1952); Proc. Roy. Soc. London A 215, 481 (1952)
[Deg99] L. Degiorgi, Rev. Mod. Phys. 71, 687 (1999)
[Dre96] M. Dressel, O. Klein, S. Donovan, and G. Gruner,¨ Ferroelectrics 176, 285 (1996)
[Dre97] M. Dressel, G. Gruner,¨ J.E. Eldridge, and J.M. Williams, Synth. Met. 85, 1503 (1997)
[Efr75] A.L. Efros and B.I. Shklovski, J. Phys. C: Solid State Phys. 8, L49 (1975) [Ehr63] H. Ehrenreich, H.R. Philipp, and B. Segall, Phys. Rev. 132, 1918 (1963)
[Ehr66] H. Ehrenreich, Electromagnetic Transport in Solids: Optical Properties and Plasma Effects, in: The Optical Properties of Solids, Proceedings of the International School of Physics ‘Enrico Fermi’ 34, edited by J. Tauc (Academic Press, New York, 1966)
[Fri56] J. Friedel, Can. J. Phys. 34, 1190 (1956)
[Gay95] A. Gaymann, H.P. Geserich, and H.v. Lohneysen,¨ Phys. Rev. B 52, 16 486 (1995)
[Gre91] N. Grewe and F. Steglich, Heavy Fermions, in: Handbook on the Physics and Chemistry of Rare Earths 14, edited by K.A. Gschneider and L. Eyring (Elsevier, Amsterdam, 1991)
[Gru74a] G. Gruner,¨ Adv. Phys. 23, 941 (1974)
[Gru74b] G. Gruner¨ and A. Zawadowski, Rep. Prog. Phys. 37, 1497 (1974) [Hel01] E. Helgren, M. Scheffler, M. Dressel, and G. Gruner,¨ unpublished
[Her83] G. Hertel, D.J. Bishop, E.G. Spencer, J.M. Rowell, and R.C. Dynes, Phys. Rev. Lett. 50, 743 (1983)
|
Further reading |
337 |
[Joy70] |
R.R. Joyce and P.L. Richards, Phys. Rev. Lett. 24, 1007 (1970) |
|
[Kit63] |
C. Kittel, Quantum Theory of Solids (John Wiley & Sons, New York, 1963) |
|
[Kun62] |
C. Kunz, Z. Phys. 167, 53 (1962); ibid. 196, 311 (1966) |
|
[Lee85] |
P.A. Lee and T.V. Rahmakrishna, Rev. Mod. Phys. 57, 287 (1985) |
|
[Lee00] |
H.-L. Lee, J.P. Carini, D.V. Baxter, W. Henderson, and G. Gruner,¨ Science 287, |
|
|
5453 (2000) |
|
[Lee01] |
M. Lee and M.L. Stutzmann, Phys. Rev. Lett. 87, 056402 (2001) |
|
[Loh98] |
H.v. Lohneysen,¨ Phil. Trans. Roy. Soc. (London) A 356, 139 (1998) |
|
[Lyn85] D.W. Lynch and W.R. Hunter, Comments on the Optical Constants of Metals and an Introduction to the Data for Several Metals, in: Handbook of Optical Constants of Solids, Vol. I, edited by E.D. Palik (Academic Press, Orlando, FL, 1985), p. 275
[McK79] S.W. McKnight, S. Perkowitz, D.B. Tanner, and L.R. Testardi, Phys. Rev. B 19, 5689 (1979)
[Mar62] L. Marton, J.A. Simpson, H.A. Fowler, and N. Swanson, Phys. Rev. 126, 182
|
(1962) |
[Miy89] K. Miyaka, T. Masuura, and C.M. Varma, Solid State Commun. 71, 1149 (1989) |
|
[Mot61] N.F. Mott and W.D. Twose, Adv. Phys. 10, 107 (1961) |
|
[Mot68] |
N.F. Mott, J. Non Cryst. Solids 1, 1 (1968) |
[Mot69] |
N.F. Mott, Phil. Mag. 19, 835 (1969) |
[Mye68] |
˚ |
H.P. Myers, L. Wallden,´ and A. Karlsson, Phil. Mag. 68, 725 (1968) |
|
[Nor71] |
C. Norris and H.P. Myers, J. Phys. 1, 62 (1971) |
[Ott87] |
H.R. Ott and Z. Fisk, in: Handbook on the Physics and Chemistry of the |
|
Acinides 5, edited by A.J. Freeman and G.H. Lander (North-Holland, |
|
Amsterdam, 1987), p. 85 |
[Pip50] |
A.B. Pippard, Proc. Roy. Soc. (London) A 203, 98 (1950) |
[Pip57] |
A.B. Pippard, Phil. Trans. Roy. Soc. (London) A 250, 325 (1957) |
[Pip60] |
A.B. Pippard, Rep. Prog. Phys. 33, 176 (1960) |
[Rae80] |
H. Raether, Excitation of Plasmons and Interband Transitions by Electrons, |
|
Springer Tracts in Modern Physics 88 (Springer-Verlag, Berlin, 1980) |
[Reu48] G.E.H. Reuter and E.H. Sondheimer, Proc. Roy. Soc. A 195, 336 (1948) |
|
[Ros81] T.F. Rosenbaum, K. Andres, G.A. Thomas, and P.A. Lee, Phys. Rev. Lett. 46, |
|
|
568 (1981) |
[Ste84] |
G. Stewart, Rev. Mod. Phys. 56, 755 (1984) |
[Ves98] |
V. Vescoli, L. Degiorgi, W. Henderson, G. Gruner,¨ K.P Starkey, and |
|
L.K. Montgomery, Science 281, 1181 (1998) |
[Vol82] |
D. Vollhardt and P. Wolfe,¨ Phys. Rev. Lett. 48, 699 (1982) |
Further reading
[Cha90] R.G. Chambers, Electrons in Metals and Semiconductors (Chapman and Hall, London, 1990)
[Dyr00] J.C. Dyre and T.B. Schrøder, Rev. Mod. Phys. 72, 873 (2000)
[Efr85] A.L. Efros and M. Pollak, eds, Electron–Electron Interaction in Disordered Systems, Modern Problems in Condensed Matter Sciences 10 (North-Holland, Amsterdam, 1985)


