МиАПР_ПОВТ_2012 / MIAPR / MuAПP1

31

Различают задачи безусловной оптимизации и условной. Задача безусловной минимизации – различают методы:

1. Метод прямого поиска

2. Градиентный метод 1-го порядка.

3. Градиентный метод 2-го порядка.

Методы прямого поиска относятся к ГМ нулевого порядка. К ним относятся поиск по симплексу, метод поиска Хука-Дживса, метод Пауэла. К ГМ 1-го порядка относится метод Коши, метод Флетчера-Ривза. К ГМ 2-го порядка относятся методы Ньютона, Марквардта, Девидона Флетчера-Пауэла.

Методы прямого поиска

Метод поиска в узлах решётки.

Метод эволюционной оптимизации(Метод Бокса).

1. Выбор х ⁽⁰⁾ – начальная точка

2. построение квадрата (сторона задается самостоятельно)

3. Вычисление

4. 

Точка с минимальным значением функции начинает выполнять роль точки х ⁽⁰⁾ – центр квадрата. На рис. 2 точка х ⁽⁰⁾ на каждой итерации выбирается в качестве начальной, уменьшается в заданное количество раз величина стороны квадрата. На рис. 1 точка х ⁽³⁾ стала центром нового квадрата. В большинстве случаев встречается комбинация рис. 1 и рис. 2

Метод симплекса.

Если в методе Бокса в качестве образца выбран квадрат, то в этом методе – правильный треугольник.

В методе строится правильный треугольник с вершинами х ⁽⁰⁾, х ⁽¹⁾, х ⁽²⁾. Вычисляется значение функции, после чего отбрасывается вершина с максимальным значением функции. В нашем примере х ⁽⁰⁾ . Относительно отбрасываемой точки строится её зеркальное отражение точка х ⁽³⁾, которое находится на прямой, проходящей через отбрасываемую точку и середину противоположного отрезка. (центр тяжести прямой х ⁽¹⁾, х ⁽²⁾) В полученном треугольнике х ⁽¹⁾ , х ⁽²⁾ , х ⁽³⁾ вычисляем значение функции только в одной точке х ⁽³⁾, после чего сравниваем значение в точках х ⁽¹⁾ х ⁽²⁾ х ⁽³⁾. На каком то этапе может произойти зацикливание, т.е. в новой точке значение функции оказывается больше, чем в предыдущих точках. Для устранения зацикливания выбирается точка с наименьшим значением функции и относительно её строится треугольник с меньшей длинной стороны.

Метод поиска Хука-Дживса

2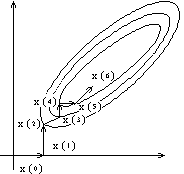 основные части:

1. Исследующий поиск

2. Поиск по образцу

Исследующий поиск. Производится вдоль координатных осей заранее заданным приращением по каждой координате. Возможны случаи успешного и не успешного поиска. В случае успешного поиска по данной координате заканчивается и начинается поиск по другой координате.

Пример:

УСПЕХ.

Поиск по образцу:

Исследующий поиск:

Останавливаемся на точке

Поиск по образу

Можно показать, что найденная точка соответствует точке минимума. Но есть - коэффициент приращения.

Метод сопряженных направлений Пауэла.

П ример:

Все методы оптимизации заключаются:

Найдем следующую точку: двигаемся в другом направлении

Изменение направления поиска:

Нормируем новое направление:

Положим

конец поиска

Градиентные методы.

Метод Каши.

- длина шага

Формула (2) используется в методе Каши. Поиск ведётся в направлении обратном градиенту. Значением определится путём решения задачи минимизации. Метод устойчивости используется в качестве начальной процедуры. При реализации градиентных методов, т.к. позволяет существенно уменьшить значение целевой функции при движении из точки, расположенной на значительном расстоянии от точки минимума.

Пример:

Поиск окончен.

Метод Фледчера-Ривса

При k=0 метод вырождается в метод Коши(начальную процедуру). Рассмотрим пример:

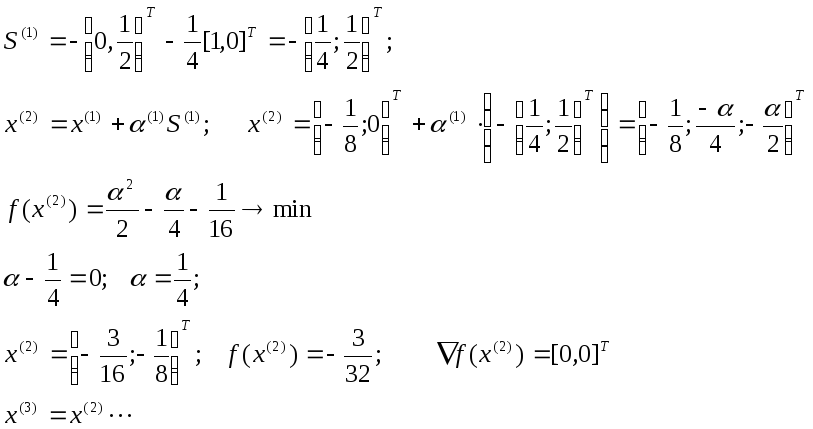
Метод Ньютона.

Модифицированный метод Ньютона.

Метод Марквардта.

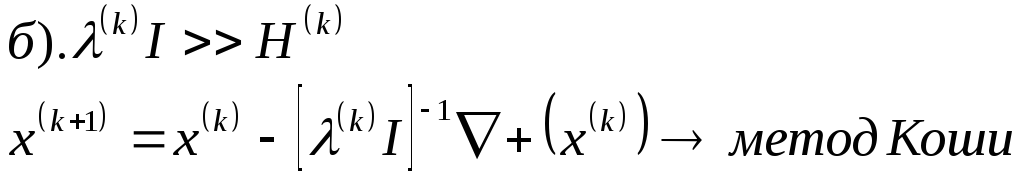
В этом методе Маркварда уменьшается величина показателя , котоорый первоначально принимается достаточно большой().

Решение задач условной оптимизации.

Метод понижения размерности.

Используется при m<n. Использование метода затр-но случае:

• большого значения m

• невозможности аналитического разрешения управления для целевой функции относительно независимой переменной

Пример 1.

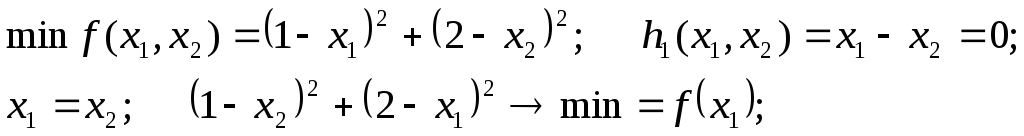
Пример 2.

Метод множителей Лагранжа

считая переменную V известной находим минимум функции для этого определяем -частные производные. Решаем полученную систему уравнений и определяем

Строим матрицу Гессе:

Для того чтобы найд. точка была точкой минимума необходимо, чтобы матрица Гессе была положительно определённой, т.е.

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5

Если матрица Гессе положительно определена, то определяем значение (). Подставляем в уравнение для ограничений значение и решаем полученное уравнение с учётом условия положительной определённости матрицы Гессе. Вычисляем окончательное значение путём подстановки выбранного значения переменной .

Задача:

найдём частные производные:

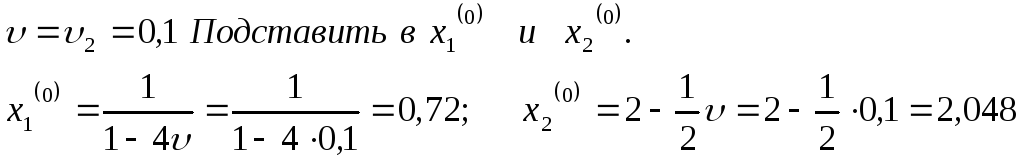
Второй способ решения задачи.

Состоит в том, что в сумме уравнений добавляется уравнение для ограничения . В результате решения системы уравнений определяется значение . Составляем матрицу Гессе в случае, если она положительно определена, то нашли точку минимума.

Случай нескольких ограничений равенств.

-два значения, которые надо исследовать

Вариант 1.

Вариант не подходит.

Вариант 2.

Методы оптимизации на основе преобразования задачи.

Квадратичный штраф.

На практике задаётся начальные значения параметра R, а за тем изменяют его так, чтобы получить наилучшее приближение к ограничениям.

R	1/R			h (x)	h (x)
	0	4,00	0	0	3
10	0,1	3,75	0,75	0,125	2,5
1	1	3,00	3	2	1
0,1	10	2,5714	4,2857	4	0,14
0,01	100	2,5075	4,4776	4,49	0,05
10		2,5000	4,500	4,5	0

Основные типы штрафных функций в случае ограничений неравенств.

Штраф типа квадрата срезки.

Пример.

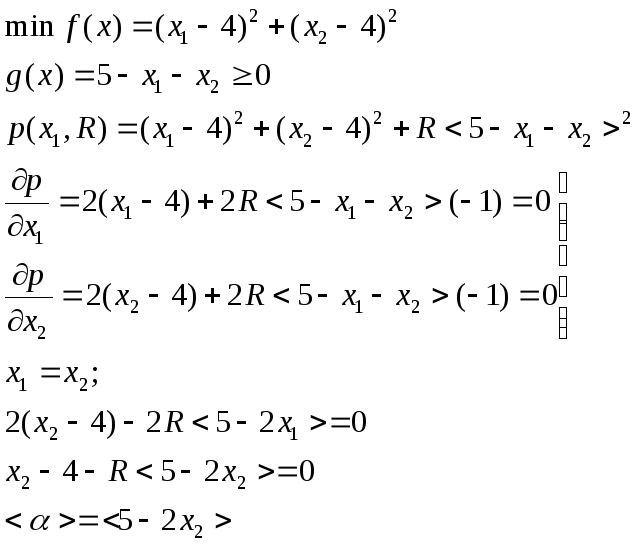
Логарифмический штраф.

Пример:

Значение отбрасывается т.к. соответствует недопустимой точке.

Штраф, выдаваемый обратной функцией.

R
100	0,59	23,3	3,83	26,13	49,43
10	1,75	10,1	1,49	6,70	16,79
1	2,23	6,2	0,53	1,88	8,12
0,1	2,41	5,0	0,18	0,56	5,61
0,01	2,47	4,7	0,06	0,17	4,85
0,001	2,49	4,6	0,02	0,05	4,61
0	2,50	4,5	0,00	0,00	4,50

Метод исключения переменных при наличии нескольких ограничений.

Метод комплекса (Бокс 1965)

В качестве модификации метода поиска по симплексу.

Наличие ограничений в задачах условий оптимизаций приводит к недопустимости отдельных точек симплекса. Их уточняют, передвигая вдоль прямой по направлению к центру тяжести. Для построения симплекса берётся начальная точка, остальные строятся случайным образом. Для каждой переменной определяются нижняя и верхняя границы, генерируются псевдослучайные числа, равномерно распределяемые на отрезке [0,1], после чего рассматриваются координаты точек.

- нижняя и верхняя граница, - псевдослучайное число.

Для получения точки в n-мерном пространстве требуется n случайных чисел. Каждая точка проверяется на допустимость. Если ограничение нарушено то точку двигают к центру тяжести уже построенных точек до тех пор, пока она не станет допустимой. Общее число точек должно быть не менее n+1. После построения множества точек в каждой из них вычисляется целевая функция. Отбрасывается точка с наибольшим значением функции. Новая точка получается путём отражения отбрасываемой точки через центр тяжести остальных точек.

Возможны случаи

1. Новая точка допустимая, но не мах. Операция отражения выполняется для мах точки.

2. Новая точка - допустимое и мах значение. Вместо отражения новую точку передвигают на половину расстояния до центра тяжести (чтобы исключить зацикливание)

3. Новая точка не допустимая. Уменьшаем в два раза состояние до центра тяжести. Процедура поиска продолжается пока многогранник не будет стянут в центре тяжести в пределах заданной точности и (или) пока разница между значениями целевой функции в вершинах не станет достаточно малой.

Бокс рекомендует значения:

Выбор компенсирует сжатие комплекса. А большее число вершин предотвращает (уплощение) и вырождение комплекса при поиске вблизи границы допустимой области.

Пусть

Так как не удовлетворяет ограничению , поэтому определяется центр тяжести для точек и .

Вновь используется генератор случайных чисел.

Имея четыре дополнительных точки, вычисляем для них значение целевой функции.

№ точки	X1	X2	F(X)	Замена точки
1	1,00	1,00	18,00
2	1,15	2,50	10,37
3	-1,20	2,00	31,04
4	0,60	3,00	12,06	3
5	2,35	2,38	5,68	1

Из таблицы видно, что исключению подлежит точка с наибольшим значением функции – точка . Определяем центр тяжести точек

В точке не выполняется ограничение , поэтому двигаем её в направлении центра тяжести.

Исключению подлежит точка . Определяем центр тяжести х…

Расчёт оформляется в виде приведённой ранее таблицы. Условие окончания поиска:

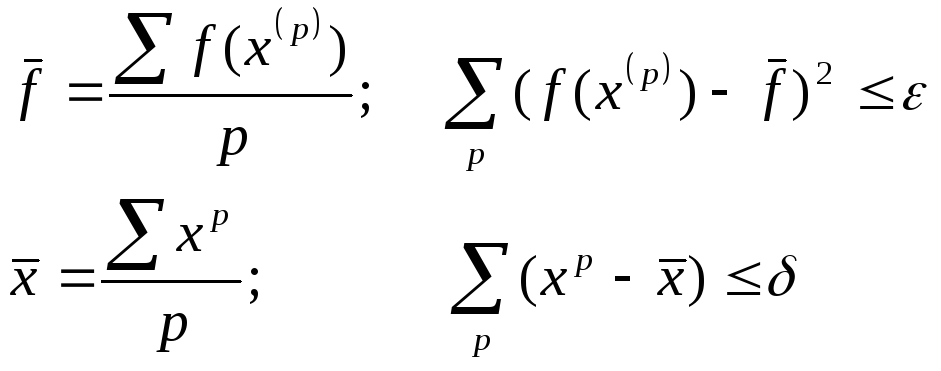
Задачи спец. структуры

Геометрическое программирование.

Разработано в 1961г. Зелиром

В геометрическом программировании имеют дело с позиномами, а с индексами n,t , может принимать различные значения. Позином отличается от много члена тем, что показатели степеней его переменных могут быть натуральными числами Для реализации поставленной задачи составляют двойственную задачу:

Пример:

Пример:

Стратегии оптимизационных исследований.

Преобразование функций и ограничений

1. - линейная функция по х.

2. Ограничения вида: .

3. 

Что позволяет иногда отбросить одно из неравенств.