Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Физика плазмы

Файл:

Цветков И. В. - Применение численных методов для моделирования процессов в плазме (2007)

.pdf

Скачиваний:

118

Добавлен:

26.08.2013

Размер:

704.97 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

f * (x, v, t) = f * (x −v t, v, 0) , что соответствует сдвигу сеточной функции по оси x на величину vj t влево или вправо, в зависимости от знака скорости в j-м узле vj (см. рис.11).

Аналитическое решение второго уравнения системы можно записать в виде f ** (x, v, t) = f ** (x, v + E t, 0) , что соответствует

сдвигу сеточной функции по оси v на величину Ei t вверх

или вниз в зависимости от знака электрического поля в i-м узле

Ei (см. рис. 11). Тогда для чис-

ленного интегрирования уравнений можно использовать следующую расчетную схему.

1. Расчет движения частиц в пространстве (вдоль оси x) определяется соотношением

vj + Ei t

xi	−vj	t x
		i

f * (t + t) = f (x −v

t, v

,t) ,

Рис. 11. Схема сеточного сдвига

то есть сводится к вычислению

значения

функции

при

x = xi −vj t с помощью интерполяции, например, линейной:

f (x

−v

t, v

,t)

= f (x ) +

f (xk +1 ) − f (xk )

где (xi −vj

t) [xk , xk +1 ] , δ = (xi

−vj t) − xk .

2. Расчет сеточной функции плотности заряда: ρi = e(n0 −nei ) ,

где nei = ∑v

fij*

t v .

j=0

3. Расчет сеточных функций потенциала и электрического поля. Для расчета значений потенциала в узлах необходимо решить

уравнение Пуассона		ϕ = −4πρ , которое в конечных разностях
имеет вид	ϕi+1 −2ϕi	+ϕi−1 = −4πρ	,	i =1..N		−1. Это уравнение
	x2	i			x
		41

соответствует системе	n = Nx −1	линейных уравнений	вида
aiϕi−1 +biϕi +ciϕi+1 = di ,	i =1..n , причем значения ϕ0 ,ϕNx		извест-
ны из граничных условий, то		есть a1 = cn = 0 . Векторно-
матричный вид системы:

b1c1 0.......0			ϕ1
a b c 0....0			ϕ	2
	2 2 2			2
	0a b c 0..0		ϕ
	3 3 3			3
........		...
	0........0a b		ϕ	n
	n n			n

=d3 .

...

dn1

В каждом уравнении отличны от нуля только элементы, лежащие на главной диагонали и на двух прилегающих к ней диагоналях. Наиболее традиционный способ решения трехдиагональной системы линейных уравнений – метод прогонки. Предполагается,

что решение удовлетворяет	условию: ϕi =αi+1ϕi+1 + βi+1 ,
i = n −1,...,1, тогда ϕi−1 =αiϕi + βi	=αi (αi+1ϕi+1 + βi+1 ) + βi и урав-
нение примет вид:

ai (αi (αi+1ϕi+1 + βi+1 ) + βi ) +bi (αi+1ϕi+1 + βi+1 ) +ciϕi+1 = di .

После приведения подобных уравнение примет вид:

ϕi+1 (aiαiαi+1 +biαi+1 +ci ) + aiαi βi+1 +αi βi +bi βi+1 −di = 0 .

Приравнивая к нулю коэффициент при ϕi+1 и сумму всех остальных слагаемых, получим систему:

aiαiαi+1 +biαi+1 +ci = 0,βi+1 (aiαi +bi ) = di −ai βi .

Из первого уравнения системы выражаем коэффициент αi+1 , из второго βi+1 :

		= −		ci
αi+1							,
αi+1				aiαi	+bi		,
				aiαi	+bi
			di −ai βi
β	i+1	=	di −ai βi			.
β		=				.
			aiαi +bi
			aiαi +bi
					42

Таким образом, все прогоночные коэффициенты αi , βi можно рассчитать, если известны α2 , β2 , они находятся из первого уравнения при i =1:

bϕ +c ϕ

= d ϕ = −

= −

, β

. Вы-

1 1 1 2

числение прогоночных коэффициентов αi , βi называется прямым

ходом прогонки. Из последнего уравнения системы определяется

ϕn :

anϕn−1 +bnϕn = dn an (αnϕn + βn ) +bnϕn = dn

ϕn = dnα−a+n βn . an n bn

Далее вычисляются ϕi−1 =αiϕi + βi , это называется обратным хо-

дом прогонки. В теории линейной алгебры доказывается, что метод прогонки можно применять при выполнении условий:

ai ≠ 0,bi ≠ 0, bi > ai + ci , αi ≤1.

Последнее условие обеспечивает устойчивость метода. Далее опре-

деляем для каждого узла xi значение поля Ei = ϕi−1 −ϕi+1 .

2 x

4. Расчет ускорения частиц, то есть расчет частиц в пространстве скоростей:

f	i, j	(x , v	,t + t) = f ** (x ,v	)		= f * (x , v	j	+ E t,t) ,
	i, j	i j	ij i j		t+ t	i	j	i
					t+ t

то есть также сводится к вычислению значений функции с помощью интерполяции, например, линейной:

f * (x , v		+ E t,t) = f * (v ) +		f * (v		) − f * (v )	δ
	j				k +1	k		v	,
									,
i		i	k			v
						v
где (vj + Ei t) [vk , vk +1 ], δv			= vj + Ei		t −vk .

4.2. Метод «водяного мешка»

Решением уравнения Власова для бесстолкновительной плазмы

= 0 является набор поверхностей cj , на которых функция рас-

f = const . Геометрическое изображение

пределения

постоянна

этих поверхностей позволяет наглядно видеть движение в фазовом

пространстве (рис.12). Любая траектория частицы на поверхности

f = const является траекторией некоторой реальной частицы. Бо-

лее того, так как

f = const , то частица не может уйти с этой по-

верхности, а значит и количество частиц внутри объема,

ограни-

ченного этой поверхностью, сохраняется: ∫ fdvdr =const . Количе-

ство частиц в объеме между любыми такими поверхностями также

постоянно:

∫ fdvdr =const .

Таким образом, плазму можно рас-

Vij

сматривать как идеальную несжимаемую жидкость в фазовом 2N

пространстве (N – размерность задачи). В эту жидкость как бы

«вморожены» поверхности f = const , так что количество жидко-

сти

между

контурами

внутри каждого

контура

сохраняется, а сами они

никогда не пересекаются.

Рассмотрим

применение

«метода водяного мешка»

для

описания пучковой

неустойчивости.

Ограни-

чимся одномерным случа-

Рис. 12. Фазовые поверхности

ем. Функцию распределе-

ния двух потоков аппроксимируем двумя прямоугольниками, тогда

начальное состояние функции

распределения задается

в виде

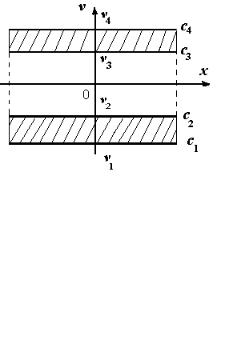
(рис. 13):

1, (x, v) V ,V ,

fe (x, v, 0)

1,2

3,4

0, (x, v) V1,2 ,V3,4 .

Объем между контурами c1 и c2 , c3 и c4		должен сохраняться:
∫ dvdx = const ,	∫ dvdx = const , то есть	имеем два «водяных
V1,2	V3,4

мешка» (рис.14). Так как частицы не покидают выделенный объем между контурами, то для определения динамики контура не обязательно следить за частицами в объеме, достаточно следить за границей объема, то есть за

частицами

на

границе.

На каждом шаге по вре-

мени по положению на-

ходящихся

на

границе

частиц

можно

путем

интерполяции

восста-

навливать

геометрию

границы

объема.

Для

расчета

движения

час-

тиц необходимо рассчи-

тать

электрическое

по-

Рис. 13. Начальная функция

ле,

решив

уравнение

распределения

Пуассона

∂E

=1− ∞∫

fdv (уравнение записано в безразмерных величинах). В

∂x

−∞

точке положения i-й частицы xi поле определяется интерполированием значений поля в ближайших узлах пространственной сетки

xk и

ния

xk +1 . Электрическое поле в узлах рассчитывается из уравне-

xk+1	∞	xk+1	∞
Ek +1 − Ek = ∫	(1− ∫ fdv)dx =	x − ∫	∫ dvdx .
xk	−∞	xk	−∞

Второе слагаемое правой части представляет собой площадь фигуры, которую можно вычислить как разность криволинейных трапе-

ций между прямыми x = xk , x = xk +1 и контурами, то есть, равно

разности значений скорости на верхнем и нижнем контуре, умноженной на x (рис.12). Координаты и скорость i-й частицы в следующий момент времени:

Рис. 14. Движение контуров в фазовом пространстве

xi (t + t) = xi (t) +vi (t) t,vi (t + t) = vi (t) − Ei (t) t.

Если точки контура на очередном шаге так сильно расходятся, что восстановление контура становится неоднозначным, то прежде чем восстановить геометрию контуров на следующем шаге, необходимо увеличить количество частиц на контуре, поместив на нем дополнительные частицы. Был рассмотрен случай прямоугольной функции распределения, непрерывная функция распределения может быть представлена в виде ступенчатой функции, каждый прямоугольник которой представляет собой один «водяной мешок». Таким образом, идея модели «водяной мешок» состоит в том, что непрерывная функция распределения f (r, v,t) представляется

в виде набора некоторого количества «водяных мешков» с подвижными границами, но постоянным фазовым объемом.

5.МЕТОД КРУПНЫХ ЧАСТИЦ

5.1.Описание метода

Рассмотрим дискретное моделирование плазмы на примере численного решения уравнения Власова методом крупных частиц:

dfα	=	∂fα	+v	∂fα	+	eZα	(E +	1 v ×H )	∂fα	= 0 .
dt		∂t		∂r					∂v
						m		c
						α

Фазовое пространство (r, v) для каждой компоненты в начальный момент времени разбивается на ячейки. В соответствии с начальной функцией распределения каждой компоненты fα (r , v, 0) счи-

тается число частиц в каждой ячейке. Затем суммируются заряды и массы всех частиц данного сорта, содержащиеся в одной ячейке, суммарный заряд и масса присваиваются одной модельной частице данного сорта, которую помещают в узел сетки. Таким образом, есть не только начальное распределение макрочастиц, но и есть в каждом узле начальное значение плотности заряда и тока. Далее рассчитываются электрическое и магнитное поле по имеющимся значениям заряда и тока в узлах. После этого рассчитывается движение макрочастиц, их новое положение в фазовом пространстве в следующий момент времени. Таким образом, определяется текущая функция распределения. Затем заряды частиц вновь разносятся по узлам фазового пространства, и процесс повторяется. Данный процесс можно представить в виде схемы, связывающей семь задач

(рис. 15).

Задача 1. Формирование на-
чального состояния макрочас-
тиц ri (0), vi (0)
тиц ri (0), vi (0)					Задача 6. Расчет движения
					заряженных частиц для
					заряженных частиц для
					определения их положения
Задача 2. Вычисление			Задача 7. Восстановле-		в следующий момент
Задача 2. Вычисление			Задача 7. Восстановле-		времени ri (t + t) ,
плотностей заряда и			ние функции распреде-
тока в узлах сетки			ления fα (t + t)
тока в узлах сетки						vi (t + t)
ρ		(t), j (t)
ρ	k	(t), j (t)
	k	k

Задача 3. Расчет по-			Задача 4. Расчет электрическо-			Задача 5. Расчет
тенциалов в узлах			го и магнитного поля в узлах			сил, действующих
		сетки		сетки Ek (t), Bk (t)		на макрочастицы
ϕk (t), Ak (t)				сетки Ek (t), Bk (t)		Fi (t)
ϕk (t), Ak (t)						Fi (t)

Рис. 15. Общая схема метода крупных частиц

Метод крупных частиц по сравнению с методом молекулярной динамики позволяет, во-первых, существенно уменьшить число частиц, во-вторых, избежать сингулярности кулоновских сил, обратно пропорциональных квадрату расстояний между частицами

( r12 ). Однако необходимо обоснование возможности использо-

вания данного метода для моделирования плазмы.

Обоснование метода

1. Так как суммарные плотности зарядов и масс макрочастиц и реальных частиц равны e′n′ = en и m′n′ = mn , то отношение заря-

да и массы макрочастицы и реальной частицы одинаковы me′′ = me ,

азначит, тождественна динамика реальной и макрочастицы.

2.Плазменные частоты системы макрочастиц и реальных час-

	′ ′2		2
тиц равны ω0′e,i =	4πn ee,i	=	4πnee,i	=ω0e,i , то есть сохраняется

	me′,i		me,i

характерное время плазменных процессов.

3. Если положить, что тепловые скорости равны, то дебаевские

радиусы		системы			макрочастиц		и реальных	частиц равны
rd′ =	vТ′	=	vТ	= rd ,	то	есть	сохраняется	характерный
	ω′		ω
	0e		0e

пространственный размер.

Несмотря на эти совпадения характерных параметров системы макрочастиц и реальных заряженных частиц, необходимо следить за выполнением следующих трех условий:

1)	условие квазинейтральности системы: rd								lхар ;
2)	условие			идеальности				системы:	ND 1,	где
		4		kT ′		3/ 2	′
	ND =		π(		)	n	− число макрочастиц в дебаевской
	ND =	3	π(	′ ′2	)	n	− число макрочастиц в дебаевской
		3		4πn e

сфере, которое называется числом Дебая;

3)шаг интегрирования должен быть много меньше минимального характерного времени процессов в плазме, то есть

времени электронных колебаний t τ	p	=	1	.

			ω
			0e

Первое условие соответствует критерию того, что систему заряженных частиц можно назвать плазмой. Второе условие соответствует условию пренебрежения потенциальной энергии взаимодействия отдельных частиц по сравнению с кинетической энергией

Wк	Wп , то есть соответствует расчету бесстолкновительного

уравнения Власова, когда коллективное поле частиц существенно больше поля межчастичного взаимодействия. Третье условие обеспечивает как устойчивость расчетной схемы, так и адекватность результатов плазменным процессам.

Рассмотрим вычислительный цикл метода крупных частиц на примере электростатической задачи (без магнитного поля).

Первая задача − задание начального распределения, соответствующего нужному типу старта (холодная плазма, спокойный старт, хаотический старт и т.п.) и нужному распределению частиц, была рассмотрена ранее достаточно подробно для метода молекулярной

динамики.

Вторая задача – вы-

числение

плотностей

заряда

и тока в узлах

xk −1

ρk

(xi )

xk +1

сетки.

Самый

простой

метод

взвешивания

–

«ближайший

узлу

сетки» (NGP – nearest

grid

point),

состоит

xk −1

xk +1

подсчете числа

частиц

данного сорта, находящихся в

данный момент времени на

отрезке

x −

; x +

xk −1

xk +1

ρk (x

i )

это количество частиц, умно-

женное на заряд данного сор-

та частиц, присваивается k-му

xk −1

xk +1

узлу как заряд данного сорта

частиц. Суммирование заря-

Рис. 16. Способы взвешивания

дов по всем сортам частиц

дает суммарный заряд в k-м

узле. Однако при таком способе взвешивания получается макрочастица, сеточная функция плотности заряда которой имеет вид прямоугольника, то есть скачкообразна (рис.16). Макрочастица мгновенно появляется в узле и мгновенно исчезает, при этом она как бы «прыгает» между узлами. Скачкообразное изменение плотности заряда при прохождении узла приводит к «нефизическим» шумам в пространстве и во времени. Второй метод взвешивания – «облако в ячейке» (CIC – cloud in cell) – предполагает разнесение заряда по узлам с помощью линейной интерполяции:

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

Соседние файлы в предмете Физика плазмы