
- •Radio Engineering for Wireless Communication and Sensor Applications
- •Contents
- •Preface
- •Acknowledgments
- •1 Introduction to Radio Waves and Radio Engineering
- •1.1 Radio Waves as a Part of the Electromagnetic Spectrum
- •1.2 What Is Radio Engineering?
- •1.3 Allocation of Radio Frequencies
- •1.4 History of Radio Engineering from Maxwell to the Present
- •2.2 Fields in Media
- •2.3 Boundary Conditions
- •2.4 Helmholtz Equation and Its Plane Wave Solution
- •2.5 Polarization of a Plane Wave
- •2.6 Reflection and Transmission at a Dielectric Interface
- •2.7 Energy and Power
- •3 Transmission Lines and Waveguides
- •3.1 Basic Equations for Transmission Lines and Waveguides
- •3.2 Transverse Electromagnetic Wave Modes
- •3.3 Transverse Electric and Transverse Magnetic Wave Modes
- •3.4 Rectangular Waveguide
- •3.4.1 TE Wave Modes in Rectangular Waveguide
- •3.4.2 TM Wave Modes in Rectangular Waveguide
- •3.5 Circular Waveguide
- •3.6 Optical Fiber
- •3.7 Coaxial Line
- •3.8 Microstrip Line
- •3.9 Wave and Signal Velocities
- •3.10 Transmission Line Model
- •4 Impedance Matching
- •4.1 Reflection from a Mismatched Load
- •4.2 Smith Chart
- •4.3 Matching Methods
- •4.3.1 Matching with Lumped Reactive Elements
- •4.3.4 Resistive Matching
- •5 Microwave Circuit Theory
- •5.1 Impedance and Admittance Matrices
- •5.2 Scattering Matrices
- •5.3 Signal Flow Graph, Transfer Function, and Gain
- •6.1 Power Dividers and Directional Couplers
- •6.1.1 Power Dividers
- •6.1.2 Coupling and Directivity of a Directional Coupler
- •6.1.3 Scattering Matrix of a Directional Coupler
- •6.1.4 Waveguide Directional Couplers
- •6.1.5 Microstrip Directional Couplers
- •6.2 Ferrite Devices
- •6.2.1 Properties of Ferrite Materials
- •6.2.2 Faraday Rotation
- •6.2.3 Isolators
- •6.2.4 Circulators
- •6.3 Other Passive Components and Devices
- •6.3.1 Terminations
- •6.3.2 Attenuators
- •6.3.3 Phase Shifters
- •6.3.4 Connectors and Adapters
- •7 Resonators and Filters
- •7.1 Resonators
- •7.1.1 Resonance Phenomenon
- •7.1.2 Quality Factor
- •7.1.3 Coupled Resonator
- •7.1.4 Transmission Line Section as a Resonator
- •7.1.5 Cavity Resonators
- •7.1.6 Dielectric Resonators
- •7.2 Filters
- •7.2.1 Insertion Loss Method
- •7.2.2 Design of Microwave Filters
- •7.2.3 Practical Microwave Filters
- •8 Circuits Based on Semiconductor Devices
- •8.1 From Electron Tubes to Semiconductor Devices
- •8.2 Important Semiconductor Devices
- •8.2.1 Diodes
- •8.2.2 Transistors
- •8.3 Oscillators
- •8.4 Amplifiers
- •8.4.2 Effect of Nonlinearities and Design of Power Amplifiers
- •8.4.3 Reflection Amplifiers
- •8.5.1 Mixers
- •8.5.2 Frequency Multipliers
- •8.6 Detectors
- •8.7 Monolithic Microwave Circuits
- •9 Antennas
- •9.1 Fundamental Concepts of Antennas
- •9.2 Calculation of Radiation from Antennas
- •9.3 Radiating Current Element
- •9.4 Dipole and Monopole Antennas
- •9.5 Other Wire Antennas
- •9.6 Radiation from Apertures
- •9.7 Horn Antennas
- •9.8 Reflector Antennas
- •9.9 Other Antennas
- •9.10 Antenna Arrays
- •9.11 Matching of Antennas
- •9.12 Link Between Two Antennas
- •10 Propagation of Radio Waves
- •10.1 Environment and Propagation Mechanisms
- •10.2 Tropospheric Attenuation
- •10.4 LOS Path
- •10.5 Reflection from Ground
- •10.6 Multipath Propagation in Cellular Mobile Radio Systems
- •10.7 Propagation Aided by Scattering: Scatter Link
- •10.8 Propagation via Ionosphere
- •11 Radio System
- •11.1 Transmitters and Receivers
- •11.2 Noise
- •11.2.1 Receiver Noise
- •11.2.2 Antenna Noise Temperature
- •11.3 Modulation and Demodulation of Signals
- •11.3.1 Analog Modulation
- •11.3.2 Digital Modulation
- •11.4 Radio Link Budget
- •12 Applications
- •12.1 Broadcasting
- •12.1.1 Broadcasting in Finland
- •12.1.2 Broadcasting Satellites
- •12.2 Radio Link Systems
- •12.2.1 Terrestrial Radio Links
- •12.2.2 Satellite Radio Links
- •12.3 Wireless Local Area Networks
- •12.4 Mobile Communication
- •12.5 Radionavigation
- •12.5.1 Hyperbolic Radionavigation Systems
- •12.5.2 Satellite Navigation Systems
- •12.5.3 Navigation Systems in Aviation
- •12.6 Radar
- •12.6.1 Pulse Radar
- •12.6.2 Doppler Radar
- •12.6.4 Surveillance and Tracking Radars
- •12.7 Remote Sensing
- •12.7.1 Radiometry
- •12.7.2 Total Power Radiometer and Dicke Radiometer
- •12.8 Radio Astronomy
- •12.8.1 Radio Telescopes and Receivers
- •12.8.2 Antenna Temperature of Radio Sources
- •12.8.3 Radio Sources in the Sky
- •12.9 Sensors for Industrial Applications
- •12.9.1 Transmission Sensors
- •12.9.2 Resonators
- •12.9.3 Reflection Sensors
- •12.9.4 Radar Sensors
- •12.9.5 Radiometer Sensors
- •12.9.6 Imaging Sensors
- •12.10 Power Applications
- •12.11 Medical Applications
- •12.11.1 Thermography
- •12.11.2 Diathermy
- •12.11.3 Hyperthermia
- •12.12 Electronic Warfare
- •List of Acronyms
- •About the Authors
- •Index

26 Radio Engineering for Wireless Communication and Sensor Applications
electromagnetic shield made of pure copper of thickness of 4 mm (= 6 skin depths) provides an attenuation of about −20 log (1/e )6 ≈ 6 × 8.68 dB ≈ 50 dB.
In a general case, each field component can be solved from the general Helmholtz equation:
∂2E i |
+ |
∂2E i |
+ |
∂2E i |
− g |
2 |
E i = 0, i = x , y , z |
(2.70) |
∂x 2 |
∂y 2 |
∂z 2 |
|
|||||
|
|
|
|
|
|
The solution is found by using the separation of variables. By assuming that
E i = f (x ) g ( y ) h (z ),
f ″ |
+ |
g ″ |
+ |
h ″ |
|
− g2 |
= 0 |
(2.71) |
|||
f |
|
g |
|
h |
|
||||||
|
|
|
|
|
|||||||
where the double prime denotes the second derivative. The first three terms of this equation are each a function of one independent variable. As the sum of these terms is constant (g2 ), each term must also be constant. Therefore, (2.71) can be divided into three independent equations of form f ″/f − gx2 = 0, which have solutions as shown previously.
2.5 Polarization of a Plane Wave
Electromagnetic fields are vector quantities, which have a direction in space. The polarization of a plane wave refers to this orientation of the electric field vector, which may be a fixed orientation (a linear polarization) or may change with time (a circular or elliptical polarization).
The electric field of a plane wave can be presented as a sum of two orthogonal components
E = (E 1 ux + E 2 uy ) e −jkz |
(2.72) |
where ux and uy are the unit vectors in the x and y direction, respectively. In a general case this represents an elliptically polarized wave. The polarization ellipse shown in Figure 2.6(a) is characterized by the axial ratio Emax /Emin , tilt angle t , and direction of rotation. The direction of rotation, as seen in
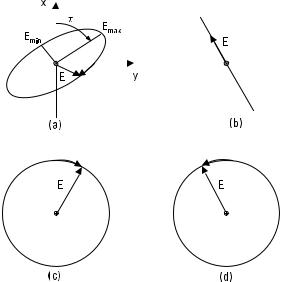
Fundamentals of Electromagnetic Fields |
27 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Figure 2.6 Polarization of a plane wave: (a) elliptic; (b) linear; (c) clockwise circular; and
(d) counterclockwise circular.
the direction of propagation and observed in a plane perpendicular to the direction of propagation, is either clockwise (right-handed) or counterclockwise (left-handed).
Special cases of an elliptic polarization are the linear polarization, Figure 2.6(b), and circular polarization, Figure 2.6(c, d). If E1 ≠ 0 and E2 = 0, we have a wave polarized linearly in the x direction. If both E1 and E2 are nonzero but real and the components are in the same phase, we have a linearly polarized wave, the polarization direction of which is in angle
t = arctan (E2 /E1 ) |
(2.73) |
In the case of circular polarization, the components have equal amplitudes and a 90° phase difference, that is, E1 = ±jE2 = E0 (E0 real), and the electric field is
E = E0 (ux − j uy ) e −jkz |
(2.74) |
or |
|
E = E0 (ux + j uy ) e −jkz |
(2.75) |

28 Radio Engineering for Wireless Communication and Sensor Applications
The former represents a clockwise, circularly polarized wave, and the latter a counterclockwise, circularly polarized wave. In the time domain the circularly polarized wave can be presented as (clockwise)
E(z , t ) = E0 [ux cos (vt − kz ) + uy cos (vt − kz − p /2)] (2.76)
and (counterclockwise)
E(z , t ) = E0 [ux cos (vt − kz ) − uy cos (vt − kz − p /2)] (2.77)
At z = 0, (2.76) and (2.77) are reduced to
E(t ) = E0 [ux cos vt ± uy cos (vt − p/2)] |
(2.78) |
2.6 Reflection and Transmission at a Dielectric Interface
Let us consider a plane wave that is incident at a planar interface of two lossless media, as illustrated in Figure 2.7. The wave comes from medium 1, which is characterized by e1 and m 1 , to medium 2 with e 2 and m2 . The planar interface is at z = 0. The angle of incidence is u 1 and the propagation vector k1 is in the xz -plane. Part E1′ from the incident field is reflected at an angle u 1′ and part E2 is transmitted through the interface and leaves at an angle of u2 .
Figure 2.7 Reflection and transmission of a plane wave in case of an oblique incidence at an interface of two lossless media: (a) parallel polarization, and (b) perpendicular polarization.

Fundamentals of Electromagnetic Fields |
29 |
According to the boundary conditions, the tangential components of the electric and magnetic field are equal on both sides of the interface in each point of plane z = 0. This is possible only if the phase of the incident, reflected, and transmitted waves change equally in the x direction, in other words, the phase velocities in the x direction are the same, or
v 1 |
|
= |
v 1 |
= |
v 2 |
|
(2.79) |
sin u |
1 |
sin u ′ |
sin u |
|
|||
|
|
1 |
|
|
2 |
||
where v 1 and v 2 (vi = v/k i ) are the wave velocities in medium 1 and 2, respectively. From (2.79) it follows
u1′ = u1 |
(2.80) |
which means the angle of incidence and angle of reflection are equal, and the angle of propagation of the transmitted wave is obtained from
sin u2 |
= √ |
m1 e1 |
(2.81) |
|
sin u1 |
m2 e 2 |
|
||
Let us assume in the following that m1 = m 2 = m 0 , which is valid in most cases of interest in practice. Then (2.81), which is called Snell’s law, can be rewritten as
sin u2 |
= √ |
e1 |
= √ |
er1 |
n 1 |
|
||||
|
|
|
|
|
= |
|
|
(2.82) |
||
sin u 1 |
e2 |
er2 |
n 2 |
|||||||
where n 1 = √er1 and n 2 = √er2 are the refraction indices of the materials. The reflection and transmission coefficients depend on the polarization of the incident wave. Important special cases are the so-called parallel and
perpendicular polarizations; see Figure 2.7. The parallel polarization means that the electric field vector is in the same plane with k1 and the normal n of the plane, that is, the field vector is in the xz -plane. The perpendicular polarization means that the electric field vector is perpendicular to the plane described previously, that is, it is parallel to the y -axis. The polarization of an arbitrary incident plane wave can be thought to be a superposition of the parallel and perpendicular polarizations.
In the case of the parallel polarization, the condition of continuity of the tangential electric field is

30 Radio Engineering for Wireless Communication and Sensor Applications
E 1 cos u1 + E 1′ cos u1′ = E 2 cos u2 |
(2.83) |
||||||
which leads, with the aid of (2.80) and (2.82), to |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
e1 |
2 |
|
|
|
||
(E 1 + E 1′ ) cos u 1 = E 2 √1 − |
|
sin |
|
u1 |
(2.84) |
||
e2 |
|
||||||
The magnetic field has only a component in the y direction. The continuity of the tangential magnetic field leads to
(E 1 − E 1′ ) √ |
|
= E 2 √ |
|
(2.85) |
e 1 |
e 2 |
From (2.84) and (2.85) we can solve for the parallel polarization the reflection and transmission coefficients, r || and t || , respectively:
|
E 1′ |
|
|
|
|
e 2 |
|
− sin2 u1 |
− |
e2 |
|
cos u1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
r || = |
= |
√e 1 |
|
|
|
|
|
|
|
|
e1 |
(2.86) |
|||||||||||||||
E 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
e 2 |
− sin2 u1 |
|
+ |
e2 |
cos u1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
√e 1 |
|
|
|
|
|
|
|
|
|
e1 |
|
||||||||||||
|
|
|
|
2 |
|
e2 |
cos u 1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
t || = |
E 2 |
|
= |
√e1 |
(2.87) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
E 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
e 2 |
− sin2 u1 |
+ |
e2 |
cos u 1 |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
√e1 |
|
|
|
|
|
|
|
e 1 |
|
||||||||||||||
When the angle of incidence is 90°, that is, when the incident wave approaches perpendicularly to the surface, it holds for r and t that
1 + r = t |
(2.88) |
In case of the perpendicular polarization, the boundary conditions lead
to
|
E 1 + E 1′ = E 2 |
(2.89) |
|||
(E 1 − E 1′ ) √ |
|
cos u1 = E 2 √ |
|
cos u2 |
(2.90) |
e1 |
e 2 |
||||
from which we can solve for the perpendicular polarization
