128 Radio Engineering for Wireless Communication and Sensor Applications
6.2 Ferrite Devices
Ferrites are ceramic materials that possess a high resistivity and that behave nonreciprocally when embedded in a magnetic field. Ferrite devices such as isolators, circulators, attenuators, phase shifters, modulators, and switches are based on these properties [3].
6.2.1 Properties of Ferrite Materials
Ferrites are oxides of ferromagnetic materials, such as iron, to which another oxide has been added as an impurity. According to their molecular structure, ferrites are divided into garnets (3M2O3 ? 5Fe2O3 ), spinels (MO ? Fe2O3 ), and hexaferrites. In garnets M is a lantanid like yttrium, gadolinium, or samarium. In spinels M is mangan, manganese, iron, zinc, nickel, or cadmium. The impurities increase the resistivity of the ferrite to as much as 1014 times higher than the resistivity of metals. Typically, the relative permittivity er is 10 to 20, whereas the relative permeability mr may be up to VHF band 1,000 or even more.
In ferromagnetic materials, strong interactions between atomic magnetic moments force them to line up parallel to each other. Ferromagnetic materials are able to retain magnetization when the magnetizing field is removed.
Atoms behave as magnetic dipoles because of the spin of their electrons. The orbital movement of the electrons about the nucleus also causes a small magnetic moment, but its effect is less important for the magnetic properties of materials. We can imagine that an electron is rotating about its axis
producing a magnetic dipole moment |
|
|
|||
| m | = |
eh |
= 9.27 |
× 10−24 Am2 |
(6.23) |
|
4p m e |
|||||
|
|
|
|
||
where e is the magnitude of the electron charge, h is Planck’s constant, and m e is the mass of an electron. The spin angular momentum of an electron is
| P | = |
h |
(6.24) |
|
4p |
|||
|
|
The vectors m and P point to opposite directions. The ratio of their magnitudes, the gyromagnetic ratio, is
Passive Transmission Line and Waveguide Devices |
129 |
||||
g = | |
m |
| = |
e |
= 17.6 MHz/gauss |
(6.25) |
|
|
||||
|
P |
m e |
|
||
A static magnetic field having a flux density B0 = B0 uz exerts on an electron a torque of (m = −g P):
T = m × B0 = −g P × B0 |
(6.26) |
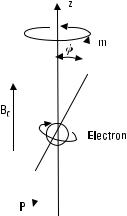
Because of this torque, the electrons and their magnetic dipoles precess as gyroscopes. The angle of precession, f, is shown in Figure 6.14. The rate of change of the angular momentum equals the torque, or d P /dt = T. Thus the equation of motion for a magnetic dipole is
d m |
= −gm × B0 |
(6.27) |
||
dt |
|
|||
|
|
|||
From this we can solve the angular frequency of precession (called the Larmor frequency):
v0 = g B0 |
(6.28) |
Let us assume that both a static magnetic field with a flux density of B0 and a field of a high-frequency wave propagating into the z direction interact with an electron. The wave is circularly polarized in the xy -plane
Figure 6.14 An electron precessing in magnetic field.
130 Radio Engineering for Wireless Communication and Sensor Applications
and has a flux density of B1 (<< B0 ). For a left-handed wave, B1 = B1− = B1 (ux + j uy ). Now the total magnetic field is tilted by an angle of u = arctan (B1 /B0 ) with respect to the z -axis and precesses with the angular frequency of the wave, v . The torque due to the field produces precession of electrons in the counterclockwise direction in synchronism with the propagating wave, and therefore f < u. From the equation of motion we solve the component of the magnetic dipole moment m − that rotates in synchronism with the left-handed circularly polarized wave
m |
− |
= |
g m 0 B1 |
(6.29) |
|
v0 + v |
|||
|
|
|
|
where m 0 = m cos f . Correspondingly, for a right-handed wave B1 = B1+ = B1 (ux − j uy ), both fields produce precession in the clockwise direction, and therefore f > u, and
m |
+ |
= |
g m 0 B1 |
(6.30) |
|
v0 − v |
|||
|
|
|
|
In ferromagnetic materials, the magnetic dipole moments are aligned parallel in regions called magnetic domains, even when no external field is present. When an external field is applied, the domains tend to orient parallel to the field. The magnetization of the material, or the magnetic dipole moment per unit volume, is M = N m, where N is the effective number of electrons per unit volume. When the external field increases, nearly all magnetic moments are aligned parallel to the field and a saturation magnetization MS is finally reached. Then the whole ferrite body behaves like a large magnetic dipole. The magnetic flux density in a saturated ferrite is
B = m0 (H0 + MS ) |
(6.31) |
As for a single electron, an equation of motion can be derived for magnetization. Equations analogous to (6.29) and (6.30) are obtained for circularly polarized waves by replacing m 0 with Nm 0 . From these it follows that the effective permeabilities for right-handed and left-handed circularly polarized waves are
|
|
|
|
S |
|
v0 |
− v D |
|
|
+ |
+ |
|
|
|
gm |
0 M S |
|
m |
|
= m 0 m r |
= m 0 |
|
1 + |
|
|
(6.32) |
Passive Transmission Line and Waveguide Devices |
131 |
|
|
|
|
S |
|
v0 |
+ v D |
|
|
− |
− |
|
|
|
gm |
0 M S |
|
m |
|
= m 0 m r |
= m 0 |
|
1 + |
|
|
(6.33) |
when B1 << B0 (small-signal conditions) and M = M S . The matrix presentation is
B + |
4 |
|
3 |
m+r |
0 |
0 |
H + |
4 |
|
3Bz |
= m 0 |
0 |
0 |
1 |
43Hz |
|
|||
B − |
|
|
0 |
m−r |
0 |
H − |
|
(6.34) |
Thus the phase constant of a right-handed wave, b + = v√em+, and that of a left-handed wave, b − = v√em −, are different.
6.2.2 Faraday Rotation
Let us consider a situation in which a plane wave propagates in ferrite in the z direction. A uniform, static magnetic field pointing to the z direction is applied over the ferrite. The wave is linearly polarized and the electric field is directed along the x -axis at z = 0. A linearly polarized wave can be divided into two orthogonal circularly polarized waves, as
E = ux E0 = (ux + |
|
E0 |
+ (ux − j uy ) |
E0 |
|
|
||||||||||
j uy ) |
|
|
|
|
|
|
(6.35) |
|||||||||
|
2 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
The phase constants of these two components are b − and b +. At |
||||||||||||||||
z = l the electric field is |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = (ux + j uy ) |
E0 |
e |
−jb −l |
+ |
(ux − j uy ) |
E0 |
e |
−jb |
+l |
(6.36) |
||||||
2 |
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
This can be written as
E = E0 e −j ( b − + b + )l /2 {ux cos [( b + − b − )l /2] − uy sin [( b + − b − )l /2]} (6.37)
The phase shift of the resultant wave is ( b − + b + ) l /2 and the tilt angle with respect to the x -axis is
132 Radio Engineering for Wireless Communication and Sensor Applications
u = arctan (Ey /Ex ) = −( b |
+ |
− b |
− |
) |
l |
|
(6.38) |
|
|
2 |
|||||
|
|
|
|
|
|
||
Hence the tilt angle of the polarization vector changes as the wave propagates in a ferrite. This phenomenon is called the Faraday rotation. A typical change is 100° per centimeter at 10 GHz.
If the direction of propagation is reversed, the tilt angle rotates in the same direction with respect to the coordinate system. Therefore, as the wave propagates back from z = l to z = 0, the tilt angle does not return back from u to 0° but its value becomes 2u. Consequently, the Faraday rotation is a nonreciprocal phenomenon.
Figure 6.15 shows how the phase and attenuation constants typically
behave in a ferrite. When v 0 > v, b + > b −, and when v0 < v , b + < b −. Thus, the direction of the Faraday rotation depends on whether the signal
frequency is smaller or larger than the resonance frequency. Close to the resonance, the attenuation constant a + is large. Well below the resonance frequency, the attenuation constant is small, but then the difference between b + and b − is small and the tilt angle rotates slowly.
Example 6.2
A linearly polarized wave at a frequency of f = 3 GHz propagates in a ferrite into the direction of a static magnetic field with a flux density B0 = 0.14 Wb/m2. The ferrite has a saturation magnetization of m 0 M S = 0.2 Wb/m2 and a relative permittivity of er = 10. Find the length of such a ferrite body that rotates the tilt angle by 90° as a wave passes through it.
Solution
Using (6.25) and (6.28) we find the resonance frequency v 0 = gB0 = 24.64 × 109 1/s. Note that 1 Wb/m2 = 1 T = 104 gauss. The angular frequency
Figure 6.15 Phase and attenuation constants for propagation in ferrite.