Добавил:

Andrey Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Электротехника

Файл:

Jack H.Integration and automation of manufacturing systems.2001.pdf

Скачиваний:

Добавлен:

23.08.2013

Размер:

3.84 Mб

Скачать

☆

<<< < Предыдущая 87 88 89 90 91 92 93 94 95 96 97 9899 / 15299 100 101 102 103 104 105 106 107 108 109 110 111 > Следующая >>>

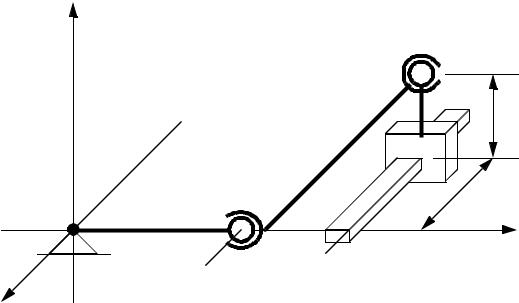
page 354

m = 6( n – 1) – 5j1 – 4j2 – 3j3 – 2j4 – j5

where,

m= mobility of the mechanism (d.o.f.)

n= number of links

j1, j2, … = the number of joints with 1, 2, ... dof respectively

• Consider the number of degrees of freedom in the linkage below,

	y
				C
				3”
				D
A		B		40”
	6”		E	40”
				x


			10”
z

12.2 HOMOGENEOUS MATRICES

• This method still uses geometry to determine the position of the robot, but it is put into an

ordered method using matrices.

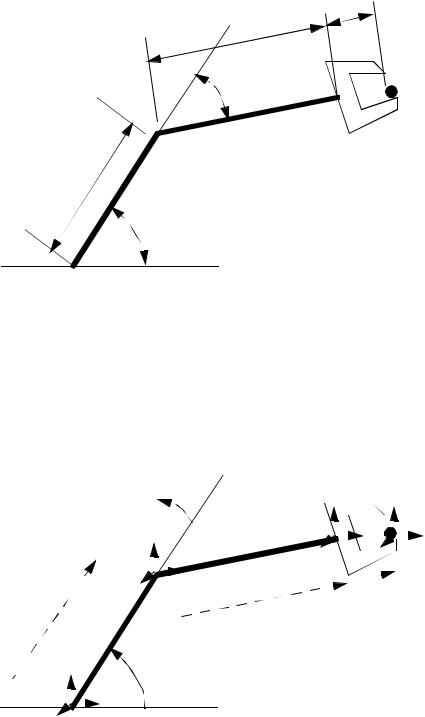
page 355

• Consider the planar robot below,

	0.2m
	1m
θ 2	TCP
θ 2	(xT, yT)

1m (x1,y1)

θ 1

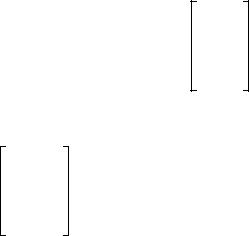
(xb, yb)

•The basic approach to this method is,

1.On the base, each joint, and the tool of the robot, attach a reference frame (most often x- y-z). Note that the last point is labels ‘T’ for tool. This will be a convention that I will generally follow.

θ 2

T0, 1

T2, T

T1, 2

θ 1

2. Determine a transformation matrix to map between each frame. It is important to do this

page 356

by assuming the joints are in their 0 joint positions. Put the joint positions in as variables.

T0, 1 =				T1, 2 =				T2, T =

1 0 0 ∆ x

trans( ∆ x, ∆ y, ∆ z) = 0 1 0 ∆ y

0 0 1 ∆ z

0 0 0 1


		1	0		0		0
rot( x, θ )	=	0	cos θ		sin θ		0
rot( x, θ )	=	0	– sin θ		cos θ		0
		0	– sin θ		cos θ		0
		0	0		0		1

		cos θ 0 – sin θ 0
rot( y, θ ) =			0	1	0		0
		sin θ		0	cos θ		0
			0	0	0		1
		cos θ		sin θ
		cos θ		sin θ		0	0
rot( z, θ )	=	– sin θ		cos θ		0	0
rot( z, θ )	=		0		0	1	0
			0		0	1	0
			0		0	0	1

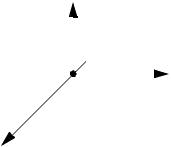
page 357

ASIDE: The structure of these matrices describe the position (P) and orientation

of the x (N), y (O), z (A), axes.

				y (O)
NX OX AX PX				y (O)
NX OX AX PX
NY OY AY PY
NZ OZ AZ PZ
					P	x (N)
					P	x (N)
0	0	0	1	z (A)
				z (A)

			cos θ				sin θ
			cos θ		1		sin θ		1	0	0	1	0	0	1
T0, 1	=	– sin θ			1	cos θ 1 0 0						0	1	0	0	= rot( z, θ	1) trans( 1, 0, 0)
				0			0			1	0	0	0	1	0
				0			0			0	1	0	0	0	1
			cos θ				sin θ

					2				2	0	0	1	0	0	1
T1, 2	=	– sin θ			2	cos θ 2 0 0						0	1	0	0	= rot( z, θ	2) trans( 1, 0, 0)
				0			0			1	0	0	0	1	0
				0			0			0	1	0	0	0	1


		1	0	0	0.2
T2, T	=	0	1	0		0		= trans( 0.2, 0, 0)
T2, T	=	0	0	1		0		= trans( 0.2, 0, 0)
		0	0	1		0
		0	0	0		1

3. Multiply the frames to get a complete transformation matrix.

page 358

T0, T = T0, 1T1, 2T2, T

			cos θ		1	sin θ	1	0 0		1 0 0 1									cos θ 2				sin θ 2 0 0				1 0 0 1			1 0 0 0.2
T0, T	=	– sin θ 1				cos θ 1 0 0				0 1 0 0								– sin θ				2	cos θ 2 0 0				0 1 0 0			0 1 0	0
		0				0		1 0		0 0 1 0										0			0	1 0			0 0 1 0			0 0 1	0
		0				0		0 1		0 0 0 1										0			0	0 1			0 0 0 1			0 0 0	1

			cos θ			sin θ												cos θ					sin θ
			cos θ		1	sin θ	1	0 0		1 0 0 1								cos θ			2		sin θ	2 0 0		1 0 0 1.2
T0, T	=	– sin θ			1	cos θ	1 0 0			0 1 0 0							– sin θ 2						cos θ 2 0 0			0 1 0			0
		0				0		1 0		0 0 1 0										0			0	1 0		0 0 1			0
		0				0		0 1		0 0 0 1										0			0	0 1		0 0 0			1

		cos θ 1				sin θ 1											cos θ						sin θ	2 0 1.2 cos θ
		cos θ 1				sin θ 1		0 0	1 0 0 1								cos θ				2		sin θ	2 0 1.2 cos θ				2
T0, T	=	– sin θ			1	cos θ 1 0 0			0 1 0 0							– sin θ					2		cos θ	2 0 –1.2 sin θ				2
		0				0		1 0	0 0 1 0											0			0	1	0
		0				0		0 1	0 0 0 1											0			0	0	1


			cos θ		1	sin θ	1	0 0		cos θ		2		sin θ						2	0	1.2 cos θ 2 + 1
T0, T	=	– sin θ			1	cos θ	1 0 0			– sin θ		2	cos θ							2 0			–1.2 sin θ 2
		0				0		1 0		0					0						1			0
		0				0		0 1		0					0						0			1

											complete the multiplication
											complete the multiplication
											and simplify to get......
	Orientation																							Position
	Orientation


				cos ( θ		1 + θ	2)	sin ( θ 1 + θ 2)								0 cos θ						1 + 1.2 cos ( θ			1 + θ 2)
T0, T =			– sin ( θ			1 + θ 2) cos ( θ 1 + θ 2)									0					sin θ		1 + 1.2 sin ( θ			1 + θ 2)
						0			0						1									0
						0			0						0									1

• The position and orientation can be read directly from the homogenous transformation

matrix as indicated above.

<<< < Предыдущая 87 88 89 90 91 92 93 94 95 96 97 9899 / 15299 100 101 102 103 104 105 106 107 108 109 110 111 > Следующая >>>

Соседние файлы в предмете Электротехника

#
23.08.2013334.86 Кб10IrWW_ULTRA_V1p0.pdf
#
23.08.2013453.11 Кб29ISO,IEC 10967-3 standard.Language independent arithmetic.pdf
#
23.08.2013196.61 Кб21ISO8601 standard.Representation of dates and times.pdf
#
23.08.20135.34 Mб289Jack H.Automating manufacturing systems with PLCs.2005.pdf
#
23.08.20135.61 Mб88Jack H.Dynamic system modeling and control.2004.pdf
#
23.08.20133.84 Mб86Jack H.Integration and automation of manufacturing systems.2001.pdf
#
23.08.2013680.22 Кб12Jackson M.A.A system development method.1982.pdf
#
23.08.2013178.08 Кб11Jackson M.JSP in perspective.2001.pdf
#
23.08.2013306.57 Кб15Jain J., Narayan A., Fujita M. - A survey of techniques for formal verification of combinational circuits (1997)(en).pdf
#
23.08.2013255.49 Кб33Jantzen J.Tuning of fuzzy PID controllers.pdf
#
23.08.2013166.76 Кб31Jantzen J.Tutorial on fuzzy logic.pdf