23. Магнитное поле прямолинейного проводника с током.

M µ

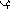
I

r A

C r₀

В на нас

N

Найдём индукцию в точке А, создаваемую проводником на расстоянии . По з-ну БСЛ для элемента имеем: ,. По принципу суперпозиции проинтегрируем последнее выражение:.С учётомполучаем:. Направление в-ра В опред прав правого винта.

Рассмотрим частный случай: Пусть есть бесконечный проводник: ф₁=0⁰, ф₂=180⁰

,

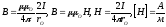
24. Определение единицы силы тока-Ампера

Найдем силу магнитного взаимодействия 2-х параллельных прямолинейных проводников с токами I₁I₂ находящимися на расстоянии х друг от друга в среде с проницаемостью µ. Пусть токи саноправлены I₁ Î Î I₂

I₂

_{, ,}

dF₁

dF₂

B₁

x

I₁

B₂

. Проинтегрируем по длине

проводника, то получаем: (*)

Если токи в одном направлении ,то они притягиваются

I₂

I₂

I₁

I₁

Выражение для силы F(*) позволяет определить единицу силы тока в СИ. Ампер равен силе неизменяющегося тока, который при прохождении по 2-ум параллельным проводникам бесконечной длины и ничтожно малой площадью кругового поперечного сечения , расположенного в вакууме на расстоянии 1 м друг от друга вызывал бы на каждом участке проводника длиной 1 м силу взаимодействия 2•10^-7 Н/м. Из последнего определения вытекает магнитная постоянная _0;

=1; I₁= I ₂=1А; l=1;x=1. Подставим в формулу(*)

2•10^-7=₀ *1*2*1*1*1/4π*1 , получаем ₀ =4•10^-7 Гн/м

25. Магнитное поле кругового тока

dl

 Найдем значение магнитного поля в точке О кругового

О

r

R

I

поля с радиусом R. По з-ну БСЛ им для эл-та тока Idl:

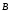
_, r=R=const

_.

Напряж магнитного поля в центре кругового витка:

B

R

I

O

r₀

Магнитный момент P_µ витка с током есть произведение

В

I

S

P_µ

силы тока I на площадь витка S: P_µ=IS, [P_µ]=А*м².

P_µ-вектор направлен как и магнитная индукция витка В

26. Закон полного тока

Закон полного тока(теорема о циркуляции вектора магнитной индукции):циркуляция вдоль замкнутого контура вектора магнитной индукции в вакууме равна произведению магнитной постоянной ₀ на алгебраическую сумму токов охватываемых этим контуром: . Выбор направления обхода контурL согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током.

,

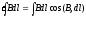I

r

B

Теорема о циркуляции вектора магнитной индукции есть следствие з-на БСЛ, но она допуск обобщение на поля и люб среды. При таком обобщении эта теорема – одно из обобщ электродинамики Максвелла: . Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.