
- •1. Электрический заряд. Дискретность заряда. Закон Кулона.
- •2. Напряженность Эл.П. Принцип суперпозиции.
- •3. Работа электростатического поля. Потенциал.
- •4. Связь напряженности с потенциалом Эл.П.
- •60 Применение теоремы Гаусса к расчету электростатических полей
- •70 Статическое поле в веществе. Электрический диполь. Поляризованные заряды. Поляризованность
- •13. Энергия электрических зарядов заряженных проводников и конденсаторов.
- •17. Законы Ома и Джоуля - Ленца в дифференциальной форме
- •18. Правило Киргоффа расчёта разветвлённых электр.Цепей.
- •20. Закон Ома в классической электронной теории
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26. Закон полного тока
- •27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
- •28. Сила Лоренца
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •31. Контур и виток с током в магнитном поле.
- •32. Явление электромагнитной индукции. Правило Ленца.
- •33. Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •36. Магнитное поле в веществе. Намагниченность.
- •37. Напряженность магнитного поля.
- •38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •41. Уравнения электродинамики Максвелла в дифференциальной форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
- •44. Интерференция света. Когерентность и монохромотичность световых волн. Оптическая длина пути. Время и длина когерентности.
- •45. Расчет интерференциальной картины двух источников
- •46. Интерференция света в тонких пленках
- •47. Дифракция света
- •48. Приближения Френеля. Метод зон Френеля.
- •49. Дифракция Френеля на угол отверстия.
- •51. Дифракционная решётка.
- •52. Принцип голографии.
- •53. Дифракция на пространственной решетке. Формула Вульфа-Брэгга.
- •54. Излучение Вавилова-Черенкова.
- •60. Дисперсия света в области нормальной и аномальной дисперсии.
- •61. Поглащение и рассеивание света
- •55. Поляризация световой волны при отражении. Закон Брюстера.
- •56. Двойное лучепреломление.
- •59° Поляроиды и поляризационные призмы.
- •58. Поляризация света. Закон Малюса .
- •59. Искусственная оптическая анизотропия. Эффект Керра.
- •62. Контактная разность потенциалов. Законы Вольта.
- •63. Термоэлектричество. Эффект Зеебека (1821).
- •64. Эффекты Пельтье и Томсона.
- •65. Пьезоэлектрический и пироэлектрический эффекты.
13. Энергия электрических зарядов заряженных проводников и конденсаторов.
 W12=(q1q2)/4πεε0r.
W12=(q1q2)/4πεε0r.
Рассмотрим теперь заряженный проводник,чтобы увеличить заряд проводника на dq надо переместить этот заряд из бесконечности на проводник и совершить при этом работу, против сил электрического поля проводника:
dA=dq(φ-φ∞)
, φ∞=0,
dA=dqφ
, dA=Cφdφ.
Эта работа идет на увеличение энергии
проводника, dA=dW,
dW=Cφdφ,
W=Cφ2/2+const.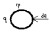
Рассмотрим
энергию заряженного конденсатора, пусть
малый заряд dq
проходит между обкладками конденсатора
тогда работа по перемещению заряда
dq/dA=Udq.
Т.к. q=CU
, dq=CdU
, dA=CUdU-это
работа по перемещению заряда ,
W=CU2/2=U2/2C=qu/2.
Если свободные зар распред непрерывно
по объёму с объёмной плотностью и по
пов-ти заряж проводн с пов-ной плотностью,
то энерг такой сист им вид:
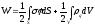

В
общем случае энергия:
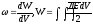
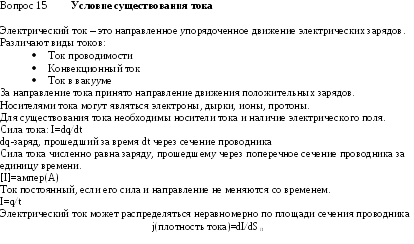
Плотность
тока числ = отнош силы тока проход через
эл площ по нормали к напр движ зар.
Плотность тока – в-р совпад с напр движ
«+» зар, напр тока в частн, если ток течёт
равномерно:
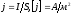
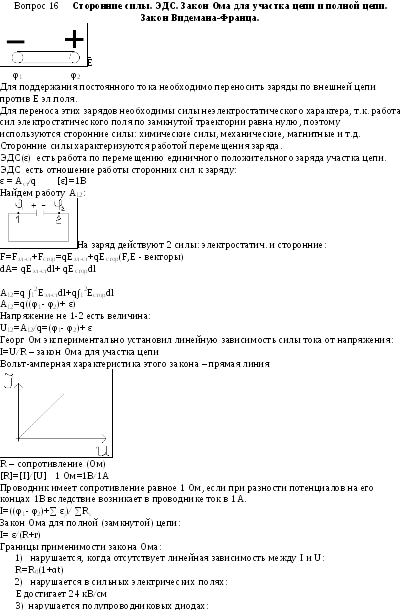
17. Законы Ома и Джоуля - Ленца в дифференциальной форме
Из Опыта известно что сопротивление R цилиндрического проводника длиною l и площадью поперечного сечения S:
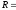 ρ
ρ
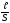 S ,
S ,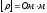


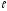
ρ
= ρ (1+αtoC),
I=
(1+αtoC),
I=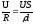 ,
I=
,
I= ∙
∙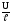 ∙S
│:S,
∙S
│:S,
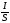 =
=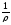 ∙
∙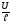
Это эквивалентно выражению: ј =σE
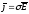 -
это закон Ома в диф.форме; если присутствуют
сторонние силы:
-
это закон Ома в диф.форме; если присутствуют
сторонние силы:
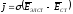
Закон Джоуля-Ленца (1841-1842)
При прохождении заряда q по участку цепи I=q/t , q=It, совершается работа A=qU=IUt
Если
проводник неподвижный и отсуствует
хим.реакции, то работа А идёт на увеличение
внутренней энергии проводника: Q=IUt.
Чаще в такой форме Q=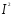 Rt.
Rt.
Если
ток переменный I=I(t):
dQ=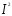 (t)Rt,
Q=
(t)Rt,
Q=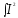 (t)Rdt
(t)Rdt
Получим
теперь закон в диф.форме(локальной
форме): Объёмной плотностью тепловой
мощности называется тепловая энергия
в единице объёма за единицу времени:
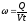
Поскольку
Q=IUt
то получим: ω =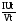 =
=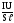 =
јE
=
јE
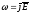 –закон
Джоуля-Ленца в диф.форме
–закон
Джоуля-Ленца в диф.форме
ω=σ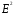 ,
т.к E=ј/σ
, ω= ρ
,
т.к E=ј/σ
, ω= ρ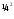
18. Правило Киргоффа расчёта разветвлённых электр.Цепей.
Рассмотрим
электр. цепь.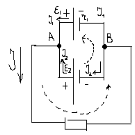
А и В - узлом называется точка в которой сходятся 3 и более проводника.
1 правило Кирхгоффа: «алгебр сумма токов сход в узле = 0»
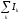 =0
=0
ток
I
входящий в узел счит «+»,
вых
«-». 
узел A: I1-I2-I=0 (1), узел B:-I1-I2+I=0 (2)
2
правило Кирхгоффа: «алгебр сумма произв
сил токов на сопротивление соотв уч
контура = алгебр сумме ЕДС в рассм
контуре»:
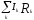 =
=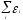 При
этом выбирают определённое направление
обхода контура, если направление тока
совпадает с направлением обхода контура
то его считают положительным. ЭДС считают
+ если при выбранном направлении ток
проходит от – к +. При этом число
независимых уравнений получается меньше
чем общее число контуров.
При
этом выбирают определённое направление
обхода контура, если направление тока
совпадает с направлением обхода контура
то его считают положительным. ЭДС считают
+ если при выбранном направлении ток
проходит от – к +. При этом число
независимых уравнений получается меньше
чем общее число контуров.
r
1
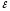 1R1
: I1r1+IR=
1R1
: I1r1+IR=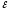 1
(3)
1
(3)
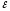 1
r 1
1
r 1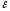 2
r 2
:I1r1-I2r2=
2
r 2
:I1r1-I2r2=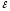 1-
1-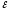 2
(4)
2
(4)
R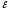 2
r
2
:I2
r2+IR=
2
r
2
:I2
r2+IR=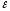 2
(5)
2
(5)
(4)+(5)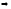 3.
(1) (3) (4) позволяют найти токиI1
I2
I
3.
(1) (3) (4) позволяют найти токиI1
I2
I

20. Закон Ома в классической электронной теории
Основные положения классической электронной теории Mе:
в Mе имеющих поликристаллическую структуру имеются свободные электроны: электроны положительности, электронный газ;
электроны участвуют в упорядоченном и хаотическом движениях. Упорядоченные движения описываются механикой Ньютона: F=ma
хаотическое движение электрона описывается моделью идеального газа, подчиняющегося классической статистике Максвелла-Больцмана.
между кристаллической решеткой Ме и электронами проводимости устанавливается тепловое равновесие.
Получим
дифференциальную форму закона Ома из
электронной связи:
плотность j связана с концентрацией электронов n, зарядом e, скоростью упорядоченного движения <v> соотношением:
j=en<v>,
I=q/t=enV/t=enSl/t=enSv, I/S=env, j=en<v>
Пусть
«е»
при соудар с узлом кристаллической
решетки полностью передает всю энергию
решетке и нач движение с vo=0.
Под действ эл-кого поля с напряженностью
E
на «е»
будет действ сила: F=eE.
Тогда «е»
приобретает ускорение: a=F/m=eE/m.
Мax
скорость электрона в конце свободного
пробега будет равна: vmax=a<τ>;
<τ>
- среднее время свободного пробега.
vmax=eE/m<τ>.
Т.к. движение электрона равноускоренное,
то скорость электрона равна:
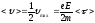 .
Ср время свободного пробега <τ>
равно отношению ср длины св проб <l>
к ср скор хаотического движения электронов
<u>:
<τ>
=<l>/<u>.
<v>=eE<l>/2m<u>.
В этом случае мы пренебрегаем скоростью
упорядоченного движения электронов в
сравнении со скоростью хаотического,
теплового движения электронов: <u>
>> <v>:
Т обр пол: j=e·n·e·E<l>/2m<u>=δE;
δ=e2n<l>/2m<u>
- электропроводность (j=
δE).
Если
бы «е»
не сталкивались с узлами решетки, то ср
длина своб пробега l=∞
и электропроводность δ=∞ и не было бы
эл-кого сопротивления. Тогда электрическое
сопротивление мет в классической
электронной теории вызвано столкновением
свободных электронов с ионами решетки.
По классической теории удельное
сопротивление ρ=1/δ пропорционально
средней скорости теплового движения
<u>:
<u>=√(8kT/2m)~√T.
из опыта вытекает, что ρ=ρо(1+αT)
.
Ср время свободного пробега <τ>
равно отношению ср длины св проб <l>
к ср скор хаотического движения электронов
<u>:
<τ>
=<l>/<u>.
<v>=eE<l>/2m<u>.
В этом случае мы пренебрегаем скоростью
упорядоченного движения электронов в
сравнении со скоростью хаотического,
теплового движения электронов: <u>
>> <v>:
Т обр пол: j=e·n·e·E<l>/2m<u>=δE;
δ=e2n<l>/2m<u>
- электропроводность (j=
δE).
Если
бы «е»
не сталкивались с узлами решетки, то ср
длина своб пробега l=∞
и электропроводность δ=∞ и не было бы
эл-кого сопротивления. Тогда электрическое
сопротивление мет в классической
электронной теории вызвано столкновением
свободных электронов с ионами решетки.
По классической теории удельное
сопротивление ρ=1/δ пропорционально
средней скорости теплового движения
<u>:
<u>=√(8kT/2m)~√T.
из опыта вытекает, что ρ=ρо(1+αT)
Классическая электронная теория расходится с опытом потому, что:
движение электронов в Ме описывается не II законом Ньютона, а уровнением квантовой механики Шредингера;
поведение эл. газа подчиняется не классической теории Максвелла-Больцмана, а Ферми- Дирака;
при низких температурах взаимодействие между электронами доминирует над взаимодействием между электронами и решеткой.
В квантовой механике электроны проявляют волновые свойства и тогда сопротивление Ме обусловлено рассеиваньем электронных волн на квантах колебаний узлов кристаллической решетки – фононах.
