3. Работа электростатического поля. Потенциал.

Пусть пробный зар. q* передвигается в Эл.п. . неподвижный зар. q на расстоянии dr и среда характеризующаяся диэлектрической проницаемостью , тогда на зар.q* со стороны поля с напряженностью Е действует переменная сила 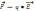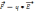. элементарная работаdA этой силы = скалярному произведению : 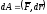, напряж поля: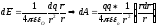,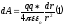. Пусть зар. перемещается из точки 1 в точку 2, тогда работа поля очевидно равна: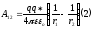. При любом выборе точек 1 и 2 работа не зависит от путей , точнее от формы траектории, а зависит от начального и конечного положения зар.q* .силовое поле такого рода называется потенциальным. Эл.п. неподвижного зар. потенциально( безвихривое ). Электростатические силы консервативны. 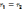Если q* перемещается по замкнутому контуру, то 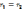, тогда. Поле потенциально, если работа сил поля по замкнутой траектории =0.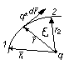

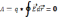
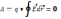
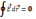
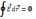. Работа сил Эл.п.dA совершается за счет убыли его потенциальной энергии dW т.е.:

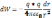
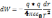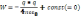
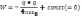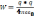
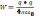dA=-dW , тгда имеем , проинтегрируем последнее выражение:,Const интегрирования =0, т.к. при интегрировании r→считается , чтоW=0, . Рассмотрим точку q.

Потенциал поля точки q на расстоянии r от зар. будет считаться равным: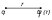

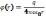
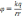
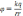
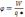
С учетом такого обозначения имеем: 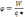. Потенциалесть скалярная энергетическая характеристика Эл.п. , численно = потенциальной энергии единичного «+» зар. в данной точке поля:=W при =+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:, где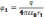

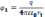
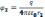
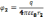
Работа сил Эл.п. при перемещении зар. численно = произведению величине этого зар. на разность потенциалов в начальной и конечной точке поля. Пусть точка 2 лежит в бесконечности, тогда можем написать:

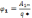
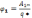. Потенциал Эл.п. численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля вк зар. Другая характеристика:

Разность потенциалов(или напряжение).

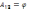
, тогда *U U=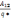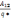- потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути.. Для потенциала справедлив принцип суперпозиции: потенциал полясистемы точечных зар. = алгебраической сумме потенциалов создаваемых отдельными зар.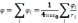

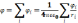
Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой 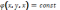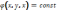, линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.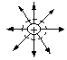

4. Связь напряженности с потенциалом Эл.П.

Пусть зар. q перемещается вдоль силовой линии оси Х из точки 1в точку 2.

работа сил поля ,

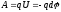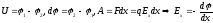
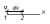
Аналогично имеем выражение для других компонентов Е:

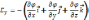
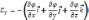, где i , j , k – орты(единичные векторы)

Его можно переписать в виде оператора Набла

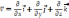
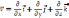выражение для Е можно написать следующим образом

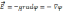
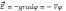имеет следующее определение:

- напряженность Эл.п. в данной точке = градиенту потенциала взятым в этой точке с обратным знаком, здесь «-» означает, что направлена в сторону убывания потенциала.

(в однородном поле)

Напряженность поля = скорости убывания потенциала по заданному направлению х.

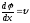
Для эл-ст поля дост знать только потенциал: