11.2 Методика профессора н.А. Калашникова.
Действующей погрешностью кинематической пары называется погрешность размеров или формы элементов пары, непосредственно проявляющаяся в работе. Понятие действующей погрешности, введенное профессором Калашниковым, является основой разработанной им теории реальных механизмов.
В высших кинематических парах, ввиду последовательного сопряжения поверхностей, должна рассматриваться непрерывно действующая погрешность.
φ
ΔFk
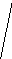
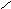
ΔFБ
ЛД
Для нахождения значения и характера изменения действующей погрешности необходимо учитывать, что взаимодействие между профилями элементов кинематической пары находят по линии действия, проходящей в каждый момент через точку взаимодействия элементов и совпадающей с направлением рабочего усилия. Для действующей погрешности характерно то, что она является комплексной, т.е. погрешностью, отражающей суммарное действие всех погрешностей звена. Комплексную действующую погрешность не следует понимать как полученную в результате суммирования отдельных первичных погрешностей. Наоборот, первичные погрешности должны рассматриваться как частные погрешности общей функциональной погрешности звена, на которые ее раскладывают.
Данная методика наиболее эффективна применительно к сложным поверхностям, получаемых кинематическим путем (кулачки, зубчатые колеса, ходовые винты и т.д.).
12. Методы отыскания коэффициентов влияния и конечных погрешностей
Коэффициент влияния – это отношение изменения сигнала на выходе измерительного устройства к вызывающей его первичной погрешности.
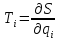
12.1.Метод дифференциальный.
Часто применяют для определения влияния различных составляющих величин на выходной сигнал, математически выраженный через величины, входящие в передаточную функцию.
Коэффициент влияния отыскивается как частная производная градуировочной характеристики идеальной измерительной цепи по соответствующему параметру.
;
;
;
;
;
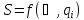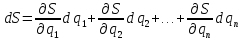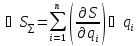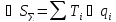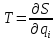Сущность дифференциального метода заключается в том, что составляются уравнения механизма, т.е. уравнения положения или перемещения ведомого звена в зависимости от координаты ведущего звена; затем дифференцированием его в частных производных, и полученный полный дифференциал есть ошибка положения или перемещения механизма.
Коэффициент влияния определяет долю влияния конкретной погрешности на суммарную.
Достоинства метода:
1.Метод является универсальным, т.е. пригоден для исследования измерительных цепей, составленных из любых преобразовательных элементов.
2.Может быть использован при исследовании группы однородных механизмов.
3.Является самым точным
Недостатки метода:
1.Требует знания градуировочной характеристики
2.С помощью метода нельзя отыскать коэффициент влияния нулевых параметров.
Указанные недостатки дифференциального метода ограничивают его применение при исследовании измерительных устройств, в которых существенное значение имеют погрешности формы кинематических элементов, их взаимное положение, т.е. те факторы, которые формируют нулевые параметры.