2. Теоремы сложения и умножения вероятностей

2.1. Теорема сложения вероятностей

Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:

.

Если события несовместные, то вероятность суммы событий равна сумме вероятностей:

.

Сумма вероятностей двух противоположных событий равна 1:

.

2.2. Теорема умножения вероятностей

Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность второго события при условии, что произошло первое событие:

.

Если события являются независимыми, то вероятность произведения событий равна произведению вероятностей этих событий:

.

Пример 2.1. Найти вероятность того, что случайно взятое двузначное число будет кратным 2 или 5.

Решение. Пусть событие А – случайно взятое число кратно 2 или 5; В – число кратно только двум; С – число кратно 5. Тогда , гдеВ и С – совместные события. Найдем вероятности этих событий.

,

,

,

Пример 2.2. Для подготовки к экзамену студентам дано 50 вопросов. Студент, готовясь к экзамену, выучил 40 вопросов. Найти вероятность того, что студент сдаст экзамен, если для сдачи необходимо ответить на 2 вопроса из двух, предложенных экзаменатором.

Решение. Пусть событие А – студент сдал экзамен; В – студент ответил на 1-й вопрос; С – студент ответил на 2-й вопрос. Тогда , событияВ и С зависимые: . Найдем вероятности, используя классическое определение вероятности.

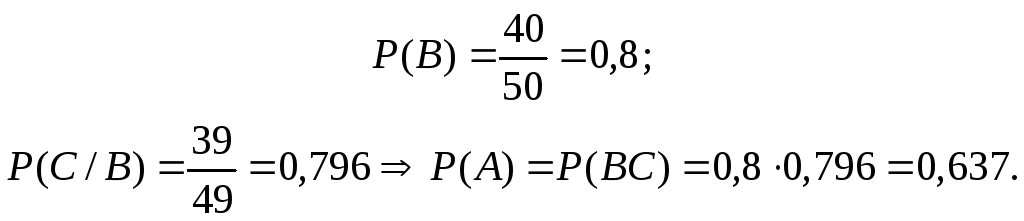
3. Формула полной вероятности. Формулы Байеса

3.1. Формула полной вероятности

События образуютполную группу событий, если они попарно несовместны и их сумма равна достоверному событию:

1) ;

2) .

Пусть событие А может наступить совместно с одним из событий , образующих полную группу, тогда вероятность событияА определяется по формуле:

.

Эта формула называется формулой полной вероятности, а события –гипотезами.

Пример 3.1. По линии связи передаются два сигнала А и В соответственно с вероятностями 0,4 и 0,6. Из-за помех 1/6 сигналов А искажается и принимается как В, а 1/5 сигналов В искажается и принимается как А. Найти вероятность того, что будет принят сигнал А.

Решение. Рассмотрим события: А – принят сигнал А, Н₁ – передавался сигнал А; Н₂ – передавался сигнал В. События Н₁, Н₂ образуют полную группу событий, поэтому

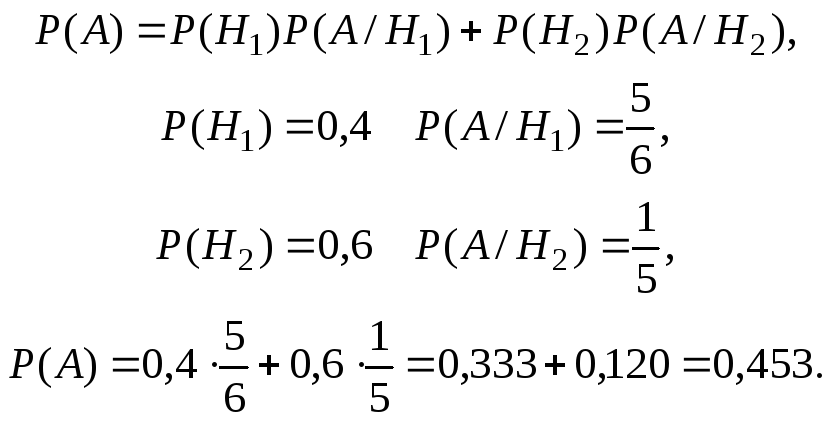
3.2. Формулы Байеса

Пусть событие А может наступить при условии появления одного из событий , которые образуют полную группу событий. Если событиеА произошло, то вероятности гипотез определяются по формулам Байеса

.

Пример 3.2. Соотношение грузовых автомобилей, проезжающих по шоссе, на котором стоит бензоколонка, к числу легковых машин, проезжающих по тому же шоссе, равно 2 : 3. Вероятность того, что будет заправляться грузовая автомашина равна 0,1; для легковой машины эта вероятность равна 0,3. К бензоколонке подъехала для заправки автомашина. Найти вероятность того, что это грузовая автомашина.

Решение. Пусть событие А – к бензоколонке подъехала для заправки автомашина; Н₁ – подъехала грузовая автомашина; Н₂ – подъехала легковая автомашина. Тогда

,

.
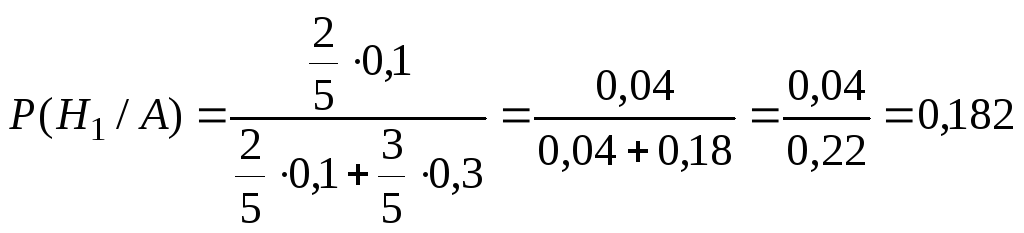