Контрольная работа №2. Требования к оформлению контрольных работ

Контрольная работа должна выполняться студентом в соответствии с номером варианта, который определяется двумя последними цифрами номера зачетной книжки студента.

При оформлении контрольной работы необходимо учитывать следующие требования:

1. на титульном листе указать номер варианта;

2. контрольные работы оформлять, оставляя поля для замечаний преподавателя;

3. условия задач необходимо записывать полностью. Если задание имеет общую формулировку, его условие необходимо переписать, подставляя числовые значения, соответствующие номеру варианта;

4. решения заданий оформлять аккуратно, приводить достаточное количество пояснений, делать необходимые рисунки.

Контрольную работу необходимо сдать за 10 дней до начала экзаменационной сессии, в противном случае студент не будет допущен к экзамену.

Решение типового варианта.

Задача 1. Найти неопределённые интегралы. В пунктах a) и b) проверить результаты дифференцированием.

1.a.

Преобразуем подынтегральную функцию таким образом, чтобы в числителе получилась производная знаменателя:

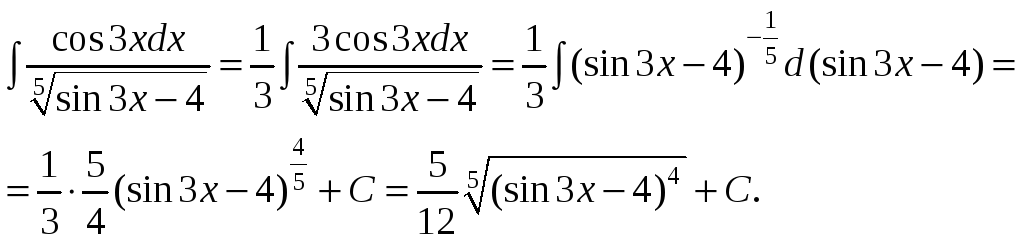
Проверим полученный результат:

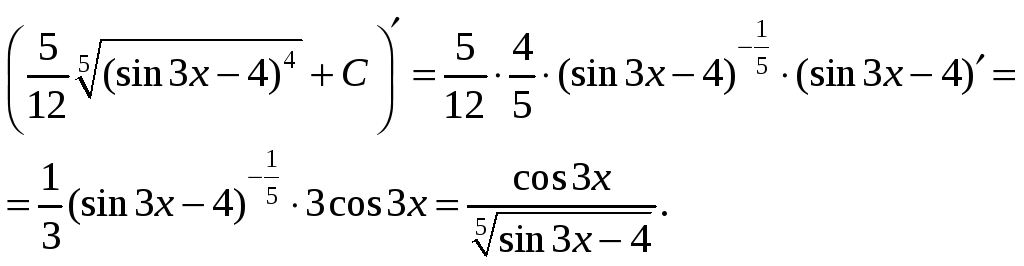
1.b.

Воспользуемся методом интегрирования по частям, основанном на следующей формуле:

Выполним проверку результата:

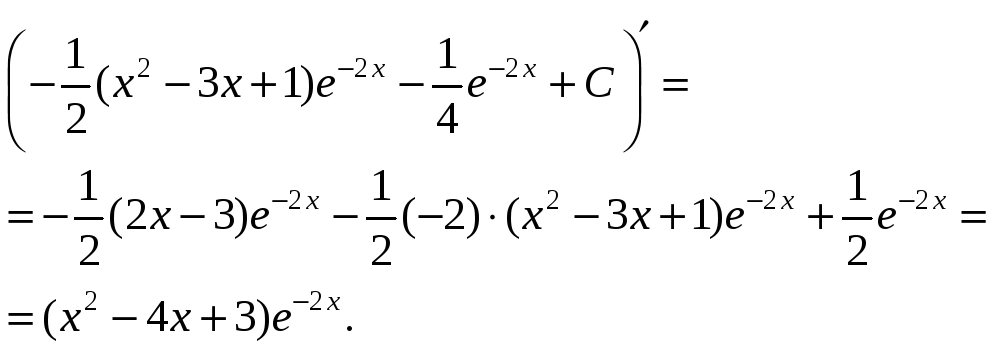
1.c.

Подынтегральная функция представляет собой рациональную дробь. Разложим её знаменатель на множители: тогда:

Приведя правую часть последнего равенства к общему знаменателю, и приравняв числители дробей, получим тождество:

Найдём искомые коэффициенты:

а) полагая , получаем , откуда ;

б) полагая , получаем , откуда ;

в) полагая , получаем , откуда ;

Подставив найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим:

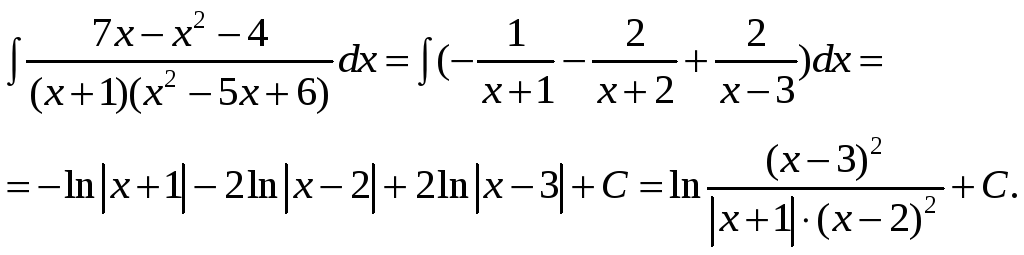
1.d.

Подынтегральная функция представляет собой интеграл вида:

Где - рациональная функция; - целые положительные числа. С помощью подстановки (здесь - наименьшее общее кратное (НОК) знаменателей ) данный интеграл приводится к интегралу от рациональной функции.

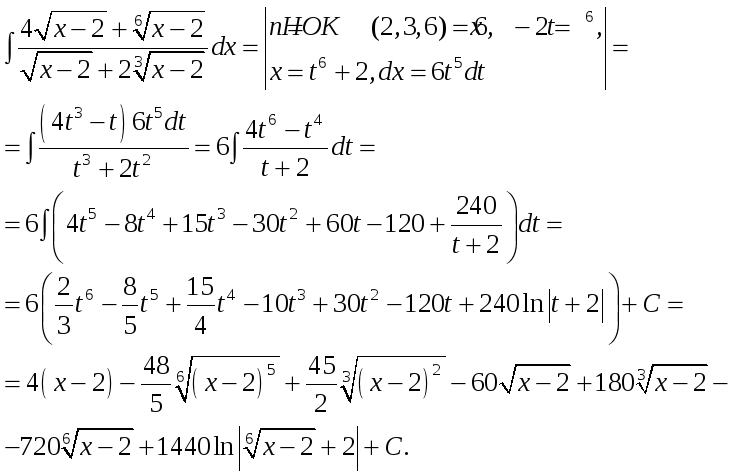
Задача 2. Вычислить приближённое значение определённого интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления производить с округлением третьего десятичного знака.

Формула Симпсона или формула парабол имеет вид:

(1)

где .

Рассмотрим

при тогда .

Составим таблицу значений подынтегральной функции, необходимых для вычисления данного интеграла.

В последней строке таблицы находятся суммы чисел соответствующих столбцов.

Так как

по формуле (1) находим

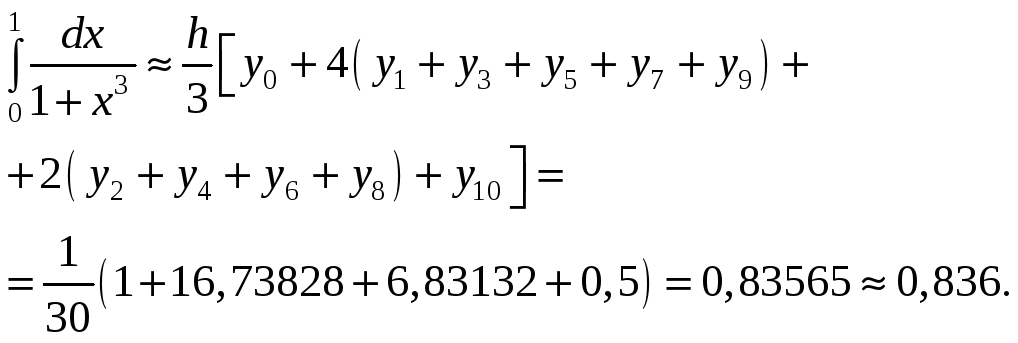
Задача 3. Вычислить несобственные интегралы или доказать их расходимость:

a)

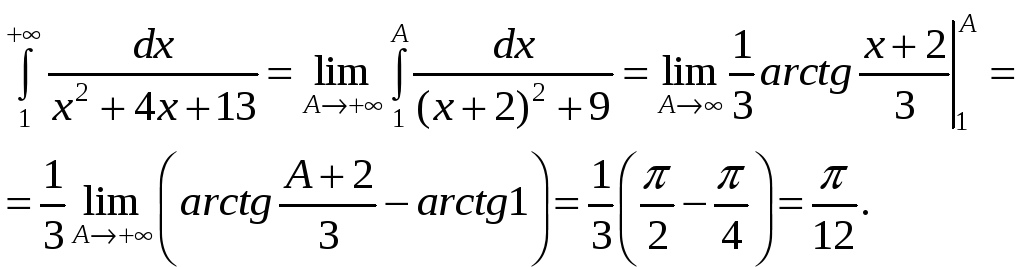
b)